- This paper consists of two sections A and B
- Answer ALL the questions in sections A and B in the spaces provided.
- All workings must be clearly shown. Mathematical tables and silent electronic calculators may be used
SECTION A (25 MARKS)
Answer ALL the questions in this section in the spaces provided
-
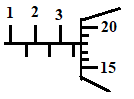
- Draw a diagram to represent a scale of a micrometer screw gauge of thimble scale 50 divisions and reading 3.68mm (2mks)
- Determine the actual reading if the micrometer screw gauge above has a zero error of 0.03mm. (1mk)
- Figure 1 shows a bimetallic strip made of brass and iron. A marble is placed at end A of the bimetallic strip as shown below:-
Fig.1
State and explain what will be observed when the bimetallic strip is strongly cooled (2mks) - State why braking systems use liquid and not gases. (1mk)
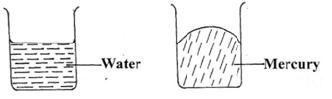
- Figure 2 shows the level of mercury and water in a beaker.
Fig. 2
Explain the difference in the shape of the meniscus (1mk) - Mercury –in-glass barometer shows a height of 70 cm. What height would be shown in the barometer at the same place if water density 1.0 x 103kg/m3 is used. (Density of mercury = 13600kgm-3) (2mks)
- Sea water of density 1.04 g/cm3 is being pumped into a tank through a pipe of uniform cross-sectional area of 3.142cm2. If the speed of water in the pipe is 5 m/s, determine the volume flux in S.I units (2mks)
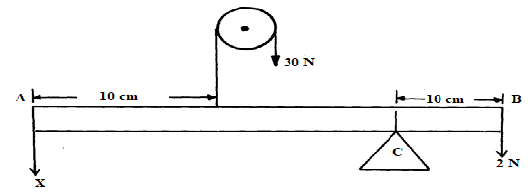
- Figure 3 shows a uniform rod AB which is 40cm long. It has a mass of 2kg and pivoted at C. If 2N is acting at point B, and 30N force is passed through a frictionless pulley.
Fig. 3
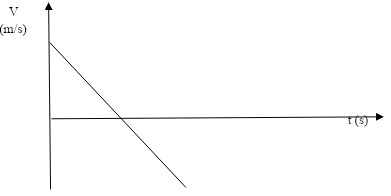
Find the force (x) acting at end A (3mks) - Sketch on the axis provided below a velocity - time graph of a motion of a stone thrown vertically upward from the edge of a platform and eventually the stone lands without bouncing on the ground below the platform. (1mk)
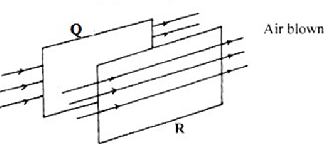
- Figure 4 shows two light sheets of paper arranged as shown.
State what is observed if strong air is blown at the same time behind paper Q and in front of paper R as shown (1mk) - A glass stopper is weighed in air then immersed wholly in water and reweighed. The readings obtained are 2.5N in air and 2.0N in water. Given that the density of water is 1000kg/m, calculate the density of the stopper. (3mks)
- State two physical quantities that remain constant while pure ice is being converted to water. (2mks)
- State the reason why thermal conductivity of a metal increases with the increase in the cross-section area of the conductor? (1mk)
- State any two characteristics of an ideal gas. (2mks)
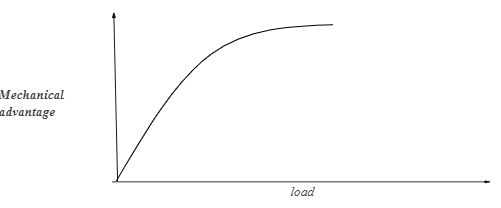
- On the grid provided, sketch a graph of mechanical advantage against load for a pulley system used to lift a load. (1mk)
SECTION B (55 MARKS)
Answer all the questions in this section.
-
- Explain why a gas exerts increased pressure when it is compressed into a small space. (2mk)
- State the law that relates the volume of a gas to the temperature of the gas. (lmk)
- A balloon is filled with air to a volume of 200 cm3 at a temperature of 293K. Determine volume when the temperature rises to 353K at the same pressure. (3mks)
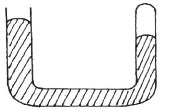
- To verify Boyle’s law a set-up consisting of a U-tube was made as shown in the figure 8 below. The tube contains mercury with air in the sealed end.
- Explain what is observed when more mercury is added. (2mks)
- Suggest a method used to maintain the temperature of air constant in the experiment. (lmk)
-
- Explain why Boyle’s law would not hold for gases such as methane. (lmk)
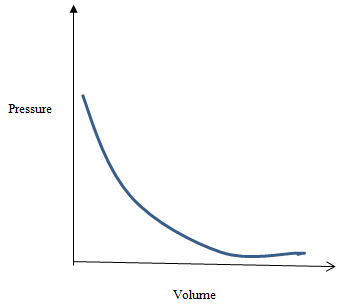
- Sketch the graph of pressure against volume for an ideal gas. (1mk)
-
- A lead shot of mass 40 g is tied to a string of length 70cm. It is swung vertically at 5 revolutions per second. Determine;
- Periodic time, (2mks)
- Angular velocity (2mks)
- Linear velocity (2mks)
- Maximum tension in the string. (2mks)
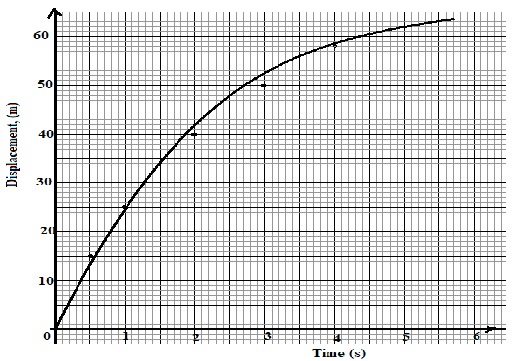
- The graph figure 5 shows displacement –time graph of an object in motion.
Fig. 5- Determine the instanteous velocities at t = 1second and at t = 4 seconds (4mks)
- Use the results in (b)(i) above to determine the acceleration of the body (3mks)
- A lead shot of mass 40 g is tied to a string of length 70cm. It is swung vertically at 5 revolutions per second. Determine;
-
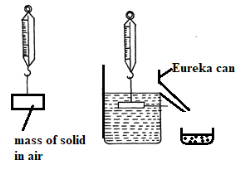
- State the Archimedes’s principle. (1mk)
- You are provided with the following apparatus;
- A spring balance
- A small piece of metal
- Eureka can
- A beam balance
- A string
- A beaker
- A retort stand
- Some water.
With the aid of a well labeled diagram, describe an experiment you would perform in the laboratory using the above apparatus to verify Archimedes’s principle for a totally immersed body. (7mks)
- A simple hydrometer has a cylindrical cross-sectional area of 2.0 cm2 and a mass of 15 g. What length of the hydrometer is immersed when it floats on water of density 1.0 g/cm3? (3mks)
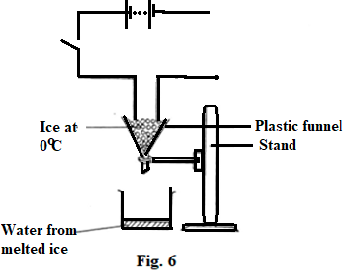
- Figure 6 shows a balloon which is filled with hot air to a volume of 200 m3. The weight of the balloon and its contents is 2200N.
Fig.6- Determine the upthrust on the balloon (density of air 0.0012g/cm3) (3mks)
-
- State two ways in which freezing point of ice can be lowered. (2mks)
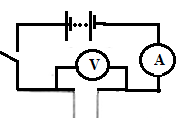
- Figure 6 illustrates an experiment in which electrical energy is used to determine specific latent heat of fusion.
- Complete the circuit to show connection of the essential circuit components. (2mks)
- Describe how the experiment can be used to determine the latent heat of’ fusion of ice. (3mks)
- A block of metal of mass 150g at 100°C is dropped into a logged calorimeter of heat capacity 40Jk-1 containing 100g of water at 25°C. The temperature of the resulting mixture is 34°C. (Specific heat capacity of water = 4200J/KgK)
Determine;-- Heat gained by calorimeter (2mks)
- Heat gained by water (2mks)
- Heat lost by the metal block (2mks)
- Specific heat capacity of the metal block (2mks)

MARKING SCHEME
-
-
- 3.68 – 0.03 =3.65mm
-
- Marble rolls down because brass contracts more than iron.
- Gases are compressible
- Adhesive forces between water molecules and glass beaker are stronger than cohesive forces between water molecules hence resultant force makes water to form a concave meniscus. Cohesive forces between mercury molecules are greater than adhesive forces between mercury molecules and glass beaker hence resultant force makes mercury form a convex meniscus.
- 0.7 x 13600 x 10 = h x 1000 x 10
h= 9.52m - Volume flux = AV
Volume = 3.142 x 102 x 5 x 10-6
Volume flux = 3.142 x 3.142 x 10-4 x 5 = 4.936 x 10-3 m3/s - For a system in equilibrium; Moment = Fd
Sum of clockwise moments = sum of anticlockwise moments
(30 x 0.1) + (2 x 0.1) = (20 x 0.1) + (x x 0.3)
6.2 – 2 = 0.3x
x = 14N -
- The papers bulge outwards away from each other. This is due to the pressure outside reducing below atmospheric pressure hence resultant outward force.
- Weight of water displaced ( upthrust)
U = WA – WW V = 0.5 W = ρvg
= 2.5 – 2.0 1000 x 10 ρ = W
= 0.5 N V = 5 x 10-5 m3 1 vg
W = ρvg Volume of water = Volume of ρ = 2.5
V = W displaced stopper 5 x 10-5 x 10
ρg ρ = 5000kg/m3 -
- Temperature
- Mass
- Increase in cross-section area increases the number of free electrons per unit length which are responsible for thermal conductivity.
-
- The size of the molecules is negligible.
- Intermolecular forces are negligible.
-
-
- The number of collisions per unit time will increase due to an increase in molecules of the gas per unit volume. Hence, the rate of change of momentum increases with the increase in number of collisions per unit time increase pressure.
- The volume of a fixed mass of a gas is directly proportional to its absolute temperature if the pressure is kept constant
- V1 = V2 V2 = 200 x 353
T1 T2 293
V2 = V1 T2 V2 = 240.96cm3
T1 -
- The volume of air at closed end decreases since more mercury exerts greater pressure resulting into reduction in volume
- Adding the mercury slowly / in little amounts to let the pressure change be slow
-
- Methane will liquify before zero volume is reached / methane is a real gas. Boyle`s law applies for an ideal gas
-
-
-
- Periodic time = 1/f
= 1/5
= 0.2 s - w = 25c+
= 2 x 3.142 x 5
= 31.42 rads-1 - Linear velocity = distance
time
C = 2πr
V = 2 x 3.142 x 0.7 x 5
15
= 21.99ms-1 - T = mg + mv2
r
= (0.04 x 10) + 0.04 x (21.99)2
0.7
= 28.03N
- Periodic time = 1/f
-
- time = 1 second;
gradient = (45 – 5 )m
(2 – 0)s
= (40) ms-1
2
= 20ms-1
t = 4 seconds
(60 – 50)m
(4.25 – 2)s
= 4.444m/s - a = v – u
t
= (4.444 – 20)ms-1
(4 – 1)s
a = −5.185ms-2
- time = 1 second;
-
-
- When a body is partially or totally immersed in a fluid, it experiences an upthrust equal to the weight of the fluid displaced.
- Tie the piece of metal with the spring and suspend it in air.
- Record its weight W1.
- Fill Eureka can with water until it flows out freely through the spout.
- Weigh an empty beaker. Put the beaker under the spout and immerse the metal partially in water.
- Wait until dripping stops and weigh the beaker with its contents.
- Record the weight of partially immersed piece of metal W2.
- Remove the object (metal) from water and repeat the experiment with a re-filled Eureka can and empty beaker (now piece of metal partially immersed.) Record weight W3.
- Weight of hydrometer = weight of water displaced
W = mg W =ρvg V = Ah
(0.015 x 10) = 1000 x 2 x 10-4 x h x 10
1000 x 20 x 10-4 1000 x 20 x 10-4
h = 0.075m -
- Upthrust = weight of air displace
W = vρg
= 200 x 1.2 x 10
= 2400N
- Upthrust = weight of air displace
-
-
- Adding impurities
- Application of pressure
-
-
-
- Arrange the apparatus as shown in the set up
- Switch on the immersion heater and start your stop watch. Note reading of ammeter and the corresponding voltmeter reading.
- After a reasonable amount of water has been collected, stop the stopwatch and note the time taken to heat the ice
- determine the mass of water collected.
- Use the equation VIt = mLf to determine Lf
-
-
- H = Cθ
= 40 JK-1 x (34 – 25) K
= 360 J - H = mcθ
= 0.1 x 4200 x 9
= 3780 J - 360 + 3780 = 4140 J
- c= Q
mθ
c= 4140
0.15 x (100−34)
c=418.18 J/kgK
- H = Cθ
-
Download Physics Paper 1 Questions and Answers - Baringo North Joint Evaluation Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students