Mathematics Paper 2 Questions and Answers - Arise and Shine Mock Exams 2022

Instructions to Candidates

• Write your name and index number in the space provided above.
• This paper consists of TWO sections: section I and section II.
• Answer all the questions in section I and only five questions from section II.
• All workings and answers must be written on the question paper in the spaced provided below each question.
• Non-programmable silent electronic scientific calculators and KNEC Mathematical tables may be used EXCEPT where stated otherwise
• Candidates should check carefully to ascertain that all the pages are printed and no questions are missing.

For Examiner’s Use Only
Section I

Section II

QUESTIONS

SECTION I: 50 MARKS

1. 1kg of brown sugar cost sh.150 while that of white sugar cost sh180. In what ratio by mass should be mixed so as to realize a profit of 20% by selling 1kg of the mixture at sh.210. (3 marks)
2. Simplify 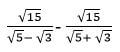 (3 marks)
3. Find the compound interest on Sh.200,000 for 2 years at 14% p.a. compounded semi-annually (3 marks)
4. Chord AB and CD in the figure below intersect externally at Q. If AB = 5cm and BQ =6cm and DQ=4cm, Calculate the length chord CD. (2 marks)
   
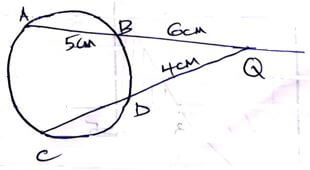
5. The ratio of 12th to 10th term in geometric series is 9:1. Find the common ratio (2 marks)
6. Make q the subject of the formula. (3 marks)
   
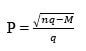
7. P varies as the cube of Q and inversely as the square root of R. If Q is increased by 20% and R decreased by 36%, find percentage change in P. (3 marks)
8. The Sketch below represents the graph of y = x² - x - 6. Find the area bounded by the curve, X-axis and the line X=5 (3 marks)
   
9.              
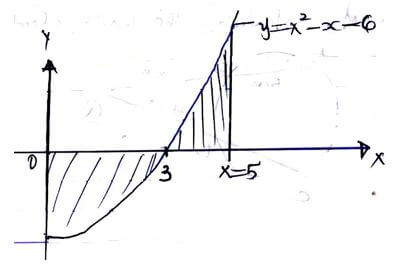
   1. Expand upto the term X³ (i) 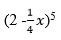(2 marks)
   2. Use your expansion to find the value of (1.96)⁵ correct to 3 decimal places. (2 marks).
10. The figure below shows a cuboid labeled ABCDEFGH point O is the mid-point of BD, AB=15cm, BC = 8cm and CF = 5cm.
    
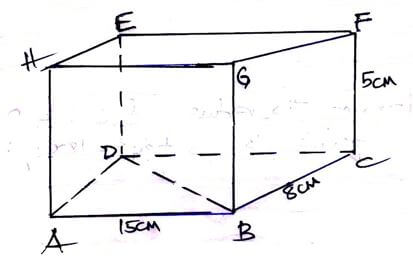
    Calculate the angle between the lines BD and EF (3 marks)
11. Find the value of X in log (X - 2) + log (X + 1) = 1 + log 4 (3 marks)
12. Given that 2 ≤ A ≤ 4 and 0.1 ≤ B ≤ 0.2. Find the minimum value of ^AB/_(A-B) (3 marks)
13. Solve the equation: 2 sin (3x+60) = 1 for 0°≤ x ≤ 180° (3 marks)
14. Determine the radius and centre of a circle whose equation is 3x² + 3y² - 18x + 12y - 9 = 0 (3 marks)
15. The position vector of A and B are given as a = 2i – 3j +4k and b = -2i – j + 2k respectively. Find to two decimal places the length of AB (3 marks).
16. In a transformation, an object with area 9cm² is mapped onto an image whose area is 54cm². Given that the matrix of transformation is 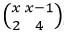 Find the value of X (3 marks)

SECTION II (50MARKS)
Choose Five Questions in this Section

17. The Points A (1, 4), B (-2, 0) and C (4,-2) of a triangle are mapped onto A¹ (7, 4), B1(X, Y) and C¹ (10, 16) by a transformation 
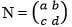
    Find;
    1. Matrix N of the transformation. (4 marks)
    2. Co-ordinates of B¹ (2 marks)
    3. A"B"C" are the image of A¹ B¹ C¹ under transformation represented by matrix 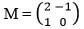 write down the coordinate of A"B"C" (2 marks)
    4. A transformation N followed by M can be represented by a single transformation K. Determine K. (2 marks)
18. The table below shows a sample of 100 bulbs, the time taken for each bulb to burn was recorded. The table below shows the results of the measurement.
    

    Time in Hrs	15-19	20-24	25-29	30-34	35-39	40-44	45-49	50-54	55-59	60-64	65-69	70-74
    Number of Bulbs	6	10	9	5	7	11	15	13	8	7	5	4

    1. Using an assumed mean of 42, Calculate;
       1. The actual mean of distribution. (4 marks)
       2. The Standard deviation of the distribution (3 marks)
       3. Calculate the quartile deviation. (3 marks)
19.                              
    1. Complete the table below by filling in the blank spaces. (2 marks)
       

       X	0	30	60	90	120	150	180	210	240	270	300	330	360
       y = cos x	1.00	0.87		0.00		-0.87		-0.87				0.87
       y = 3 sin x	0.00			3.00								-1.50	0.00

    2. Using the scale 1cm to represent 30° on the X-axis and 2cm to represent 1 unit on the vertical axis, draw on the graph y = cos x and y = 3 sin x (5 marks)
       
    3. Use your graph to solve the equation cosx - 3 sin x = 0 (2 marks)
    4. What is the difference in the value of y = cox x and y = 3 sin x at x=120° (1 mark)
20. The figure below is a triangle OAB, where OA = a andOB=b. A point R divides AB in the ratio 2:5 and a point T divides 0B in the ratio 1:3. OR and AT intersect at D.
    
    
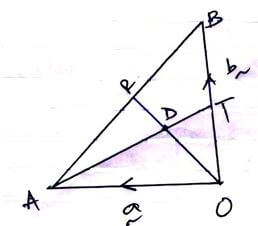
    1. Find in terms of a and b
       1. BT (1 mark)
       2. OR (1 mark)
       3. AT (1 mark)
    2. Given that AD =kAT and RD = hRO where k and h are scalars.
       1. Find the values of h and k. (4 marks)
       2. Hence AD in terms of a and b (1 mark)
21.                      
    1. Two towns on latitude 30°N are 3000km apart. Find the longitude difference of the two towns (Take π =22/7 , and radius of earth to be 6370km) (2 marks)
    2. The position of airport P and Q are P(60°N, 45°W) and Q (60°N, k°E). It takes a plane 5 hours to travel due East from P to Q at average speed of 600 knots.
       1. Calculate the value of k (3 marks)
       2. The Local time at P is 10:45am when it is the local time at Q when the plane reached there? (3 marks)
    3. Calculate the shortest distance between A( 30°S, 36°E) and B (30°S, 144°W) (2 marks)
22. A bag contains 3 red, 5 white and 4 blue balls. Two balls are picked without replacement. Determine the probability of picking.
    1. 2 red balls (2 marks)
    2. Only one red ball (2 marks)
    3. At least a white ball (2 marks)
    4. Balls of same colour. (2 marks)
    5. Two white balls (2 marks)
23. The ministry of health made an order of both Astrazenica and Johnson and Johnsons vaccines for a health centre. The total number of both vaccines should be more than 600 boxes. The number of boxes of Johnson and Johnson should be less than 500 boxes and more or equal to twice the number of Astrazenica. Letting x to represent the number of Johnson and Johnson boxes and y. to represent the number of boxes of Astrazenica,
    1.                        
       1. Form all the inequalities in x and y to represent the above information. (3 marks)
       2. Represent the inequalities on a graph (4 marks)
          
    2. If the cost of importing 1 box of Johnson and Johnson is sh1000 and astrazenica is shs.800. Find maximum cost of importing the vaccines. (3 marks)
24. A particle moves in such a way that its velocity V at any given time is v = 10t – ½t² - 15 m/s.
    1. Calculate its initial velocity (1 mark)
    2. Calculate the velocity when the time t = 3s
    3. Find the displacement during the 5th second (4 marks)
    4. Calculate the maximum velocity attained. (3 marks)

 MARKING SCHEME

1. 20% = 210
   100% = ?
   100 x 210 = 175 
   120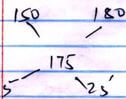
   
   1:5
2. √15(√15 + √3) - √15 (√5 - √3)
                      2
   5√3 + 3√5 - 5√3 + 3√5
                    2
   b√5
     2
   3√5
3. A = P(1 + r/100)⁴
   = 200000 (1 + r/100)⁴
   = 200000 x 1.3107960
   = sh. 262159.20
   Interest = 26159.20 - 200000
   = sh 62 159
4. 11 x 6 = (4 + x)4
   66 = 16 + 4x
   50 = 4x
   12.5 = x
   CD = 12.5 cm
5. 12th term ; ar¹¹
   10th term ; ar⁹
   ar¹¹ = 9
   ar⁹     1
   r² = 9
   r = ± 3
6. p² = nq - m
              q
   p²q - nq = -m
   q(p² - n) = -m
   q =   -m   
        p² - n
7. p = KQ³
          √R
   p1 = k(1.2 Q)³
           √0.64 R
   = 1.728 KQ³
       0.8 √ R
   = 2.16 KQ³
         √ R
   = (2.16 - 1) 180
            1
   = 116%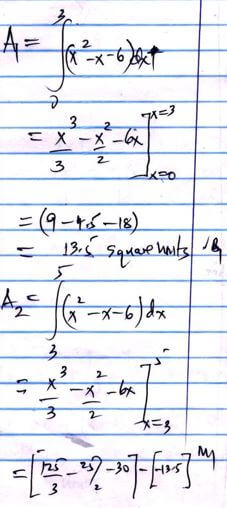
8. 
9.                          
   1. (2 - 1/4x)⁵
      co-effs; 1, 5, 10, 10
      (2 - 1/4x)⁵ = (2)⁵ - 5(2⁴) (1/4^x) + 10(2)³ (1/4x)² - 10((2)²(1/4x)³ +
      = 32 - 20x + 5x² - 5/8x³+
   2. 1.96 = 2 - 1/4x
      -0.04 = 1/4x
      0.16 = x
        5
      1.96⁵ = 32 - 20(0.16) + 5(0.16)² - 0.625(0.16)³
      = 32 - 3.2 + 0.128 - 0.0256
      = 28.9024
      =28.902
10. EF = DC
    Tan ∝ = 8/15
    ∝ = Tan^-1 (8/15)
    ∝ = 28.07º
11. Log (x² + x -2x - 2) = log 40
    x² - x -42 = 0
    x = 7   or x = -6
12.  2 x 0.1  = 0.2 
     4 - 0.1      3.9
    = 2/39
13. Sn(3x + 60) = 0.5
    3 x 60 = 30º ; 150º ; 300º
    3x = -30º ; 90º ; 330º
    x = -10º ; 30º ; 110º
    x = 30º and 110º
14. x² - 6x + y² + 4y = 3
    (x - 3)² + (y + 2)² = 3 + 9 + 4
    (x - 3)² + (y + 2)² = 4²
    centre (3,-2) and radius 4 units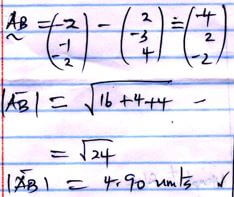
15. 
16. A.S.F = 54/9 = 6
    4x - 2 (x - 1) = 6
    x = 2
17. 

18. class	x midpoint	f freq	d	fd	d2	fd2	cf
    15-19	17	6	-25	-150	625	3750	6
    20-24	22	10	-20	-200	400	4000	16
    25-29	27	9	-15	-135	225	2025	25
    30-34	32	5	-10	-50	100	500	30
    35-39	37	7	-5	-35	25	175	37
    40-44	42	11	0	0	0	0	48
    45-49	47	15	5	75	25	375	63
    50-54	52	13	10	130	100	1300	76
    55-59	57	8	15	120	225	1800	84
    60-64	62	7	20	140	400	2800	91
    65-69	67	5	25	125	625	3125	96
    70-74	72	4	30	120	900	3600	100
    		∑f = 100		∑fd = 130		∑fd2 = 23450

    1.               
       1. mean  A + ∑fd
                            ∑f
          42 + 130/100 = 43.3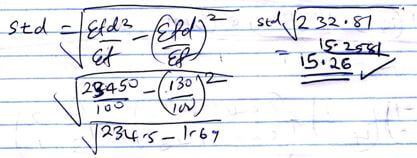
       2. 
       3. quartile deviation
          Q3 - Q1
                2
          Q3 = 49.5 + (25 - 63) ⁵
                                  13
          54.12
          Q1 = 24.9 + (25 - 16) ⁵ 
                                    9
          24.9 + 5
          29.5
          54.12 - 29.5 = 24.62
                  2                2
          = 13.13
19.                     

    1. x	0	30	60	90	120	150	180	210	240	270	300	330	360
       cos x	1.00	0.87	0.50	0.00	-0.50	-0.87	-1.00	-0.87	-0.50	0.00	0.50	0.87	1.00
       3 sin x	0.00	1.50	2.60	2.00	2.60	1.50	0.00	-1.50	-2.60	-3.00	-2.80	-1.54	0.00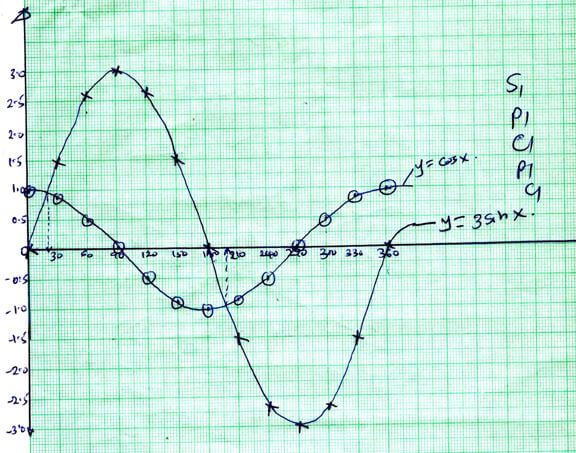

    2. 
    3. cos x - sin x = 0
       on the graph
       x = 21º ± 1
       x = 201º ± 1
    4. on the graph
       2.60 - - 1.50
       = 4.10
20.        
21.                  
    1. 3000 = 4/360 x 2 x 22/7 x 6370 cos 30o M1
       ∝= 31.15o √A1
    2.                            
       1. dist = speed x time
          = 600 x 5 √M1
          = 5000 nm
          3000 = 60∝ cos 60º √M1
          ∝ = 3000/(60 cos 60º )
          ∝ = 100º
          K = 100 - 45 = 55ºE√ A1
          Q (60º, 55ºE)
       2. longitude diff = 55 + 45
          = 100o
          Time = 100 x 4 min
          = 6 hrs 40 mins
          Time at Q = 10.45 – 6.40
          = 4.05 am
          Arrival at Q = 4.05 + 5.00
          = 9.05 am
    3. Q = 180º – 2 (30)º
       = 120º
       Distance = 60Q
       = 60 x 120
       = 7200nm
       OR in KM
       = 120/360 x 2 x 22/7 x 6370
       = 13,346.67KM
22.                    
23. 
24.