QUESTIONS
SECTION 1 (50 MARKS)
Answer all questions in this section.
- Solve for x in the equation 2Sin2x - 1 = Cos2x + Sinx for 0º ≤ x ≤ 360º(3marks)
-
- Expand (1+3/x) 5 up to the fifth term (2marks)
- Hence use your expansion to evaluate the value of (2.5)5 to 3 d.p. (2 marks)
- Complete the table below for for -4 ≤ x ≤ 2.
Hence use trapezium rule with six strips to find the area of the region bounded by the curve and the x- axis. (3marks)x -4 -3 -2 -1 0 1 2 y - Make p the subject of the formula (3 marks)
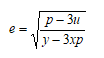
- The figure below shows a rectangular based right pyramid. Find the angle between the planes ABCD and ABV. (3marks)
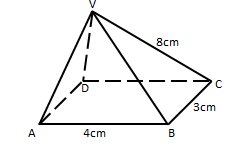
- An object A of area 10cm2 is mapped onto its image B of area 60cm2 by a transformation whose matrix is given by
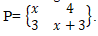 . Find the possible values of x. (3 marks)
. Find the possible values of x. (3 marks) - Find the value of x in the equation(3marks)
log105 - 2 + log1010(2x + 10) = log10(x - 4) - The data below shows marks obtained by 10 students in a test.
71, 55, 69, 45, 65, 57, 71, 82, 55, 50. Calculate the standard deviation using an assumed mean of 60. (3marks) - Evaluate by rationalizing the denominator and leaving your answer in surd form. (3marks)
√8
1 + cos45º - The position vectors fof points A and B are 5i + 4j - 6k and 2i - 2j respectively. A point X divides AB in the ratio -3: 5. Find the coordinates of X. (3marks)
- A closed box has a square base of side x metres and its height h metres. The total surface area of the box is 24m2.
- Find the expression of h in terms of x.
- Hence find the value of x that would make the volume of the box maximum. (4 marks)
- M varies directly as D and as the cube of V. Calculate the percentage change in M when V is increased by 10% and D is reduced by 10%. (3marks)
- Find the value of t if the gradient of the graphs of the functions y = x2 - x3 and y = x - tx2 are equal at x = 1/3. (3marks)
- The image of a point A, under the transformation represented by the matrix T = (10 -12) is A’ (-2, 4)Find the coordinates of A (3marks)
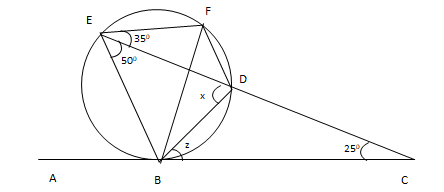
- In the figure below, ABC is a tangent at B and CDE is a straight line. BED = 50º , DEF = 35º and ECB = 25º Calculate the values of x and z. (2marks)
- The equation of a circle is given by 4x2 + 4y2 - 8x + 2y - 7 = 0Determine the coordinates of the centre of the circle. (3marks)
SECTION II (50 MARKS)
Answer only five questions from this section
-
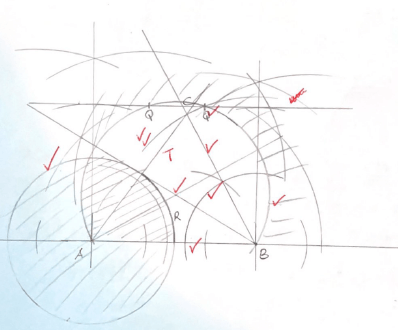
- Using a ruler and a pair of compasses only construct triangle ABC in whichAB = 6cm, BC = 5.5cm and angle ABC = 60º. Measure AC. (3marks)
- On the same side of AB as C, determine the locus of a point P such that angle APB = 60º (2marks)
- Construct the locus of R such that AR = 3cm (1mark)
- Identify the region T such that AR≥ 3cm and angleAPB≥ 60º by shading the unwanted part. (2marks)
- Determine point Q such that area of AQB is half the area of ABC and that Angle AQB = 60º. (2marks)
- A sequence is formed by adding corresponding terms of an AP and GP. The first, second and third terms of the sequence formed are 14, 34 and 78 respectively.
- Given that the common ratio of the GP is 3;
- Find the first term of the AP and GP and the common difference of the AP. (2marks)
- Find the sixth term and the sum of the first six terms of the sequence. (3marks)
- The second and third terms of a geometric progression are 24 and 12(x + 1) respectively.
Find the whole number value of x and hence the first term given the sum of the first three terms of the progression is 76. (5marks)
- Given that the common ratio of the GP is 3;
-
Income tax rate are as shown below.
Income (k£ p.a) Rate (Ksh per £) 1- 4200 2 4201 - 8000 3 8001 - 12600 5 12601 – 16800 6 16801 and above 7 Omari pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of Ksh. 10800 and is entitled to a personal relief of Ksh. 1,100 per month. Determine;- his gross tax p.a in Ksh (2marks)
- his taxable income in k£ p.a (4marks)
- his basic salary in Ksh. p.m (2marks)
- his net salary per month (2marks)
- The diagram below shows a sketch of the line y = 3x and the curve intersecting at point P and Q.
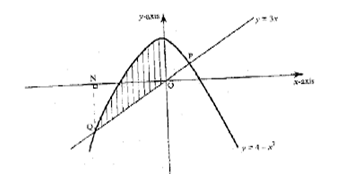
- Find the co-ordinates of P and Q (4marks)
- Given that QN is perpendicular to the x-axis at N, calculate
- The area bounded by the curve y = 4 - x2 , the x-axis and line QN. (2marks)
- the area of the shaded region that lies below the x - axis (2marks)
- the area of the region enclosed by the curve y = 4 - x2 , the line y = 3x and the y-axis (2marks)
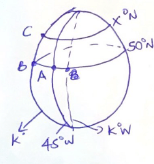
- The positions of two towns A and B are (50ºN, 45ºW) and (50ºN, KºW) respectively. It takes a plane 5 hours to travel from A to B at an average speed of 800knots. The same plane takes 1½ hours to travel from B to another town C at the same average speed. Given that C is to the north of B, calculate to the nearest degree,
- The value of K (4marks)
- The latitude of C (3marks)
- If the plane started from A at 9.00am and flew to C through B, find the local time at C when the plane arrived there. (3marks)
-
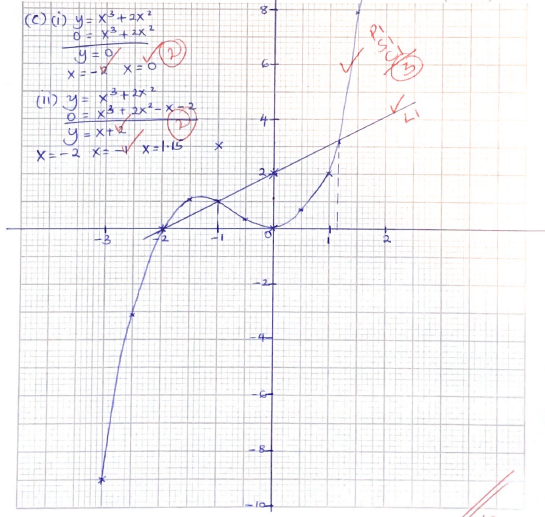
- Complete the table below for the equation y = x3 + 2x2 to 2 d.p(2marks)
x -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2x2 18 12.5 8 4.5 2 0 1 4.5 x3 -27 -8 -1 0 1 y -9 0 1 0 2 - On the grid provided, draw the graph of y = x3 + 2x2 for -3 ≤ x ≤ 1.5. Take a scale of 2cm to represent 1 unit on the x- axis and 1cm to represent 1unit on the y – axis. (3marks)
- Use your graph to solve
- x3 + 2x2 = 0(2marks)
- x3 + 2x2 - x - 2 = 0(3marks)
- Complete the table below for the equation y = x3 + 2x2 to 2 d.p(2marks)
- The table below shows the marks obtained by 47 students in a mathematics test.
Marks 31-35 36-40 41-45 46-50 51-55 56-60 No. of candidates 4 6 12 15 8 2 - On the grid provided, draw a cumulative frequency curve. (3marks)
- Use your graph to estimate
- The median (2marks)
- The semi interquartile range (2marks)
- In order to pass the test a candidate had to score more than 40 marks. Calculate the percentage of candidates who passed. (3marks)
- In the triangle OPQ below, OP = p and OQ = q. R is a point on PQ such that PR: RQ = 1 : 3 and 5OS = 2 OQ. PS intersects OR at T.
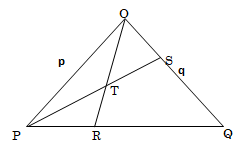
- Express in term of p and q
- OS (1mark)
- PQ (1mark)
- OR (2mark)
- Given that OT= hOR and PT = kPS. Determine the values of h and k. (6marks)
- Express in term of p and q

MARKING SCHEME
- 2sin2x - 1 = 1 - sin2x + sinx
2sin2x + sin2x - sinx - 1 - 1 = 0
3sin2x - sinx - 2 = 0
3sin2x - 3sinx + 2sinx - 2 = 0
3sinx(sinx - 1) + 2(sinx - 1) = 0
(sinx - 1)(3sinx + 2) = 0
sinx - 1 = 0 or 3sinx = -2/3
3
sinx = 1 sinx = -2/3
x = 90 x = 180 + 41.81 = 138.19
x = 360 - 41.81 = 318.19 -
- 1 + 5(3/x) + 10(3/x)2 + 10(3/x)3 + 5(3/x)4
1 + 15/x + 90/x2 + 270/x3 + 405/x4 - 2.5 = 1 +3/x
2.5 - 1 = 3/x
1.5 = 3/x
1.5x/1.5 = 3/15
1 + 15/2 + 90/4 + 270/8 + 405/16
= 90.0625
= 90.63
- 1 + 5(3/x) + 10(3/x)2 + 10(3/x)3 + 5(3/x)4
A = x 1{0 + 0 + 2(5 + 8 + 9 + 8 + 5)}x -4 -3 -2 -1 0 1 2 y 0 5 8 9 8 5 0
= x 2(35)
= 35- e2/1 = p - 3u
y - 3xp
e2(y - 3xp) = p - 3u
e2y - 3e2xp = p - 3u
e2y + 3u = p + 3e2xp
p + 3e2xp = e2y + 3u
p(1 + 3e2x) = e2y + 3u
p = e2y + 3u
1 + 3e2x -
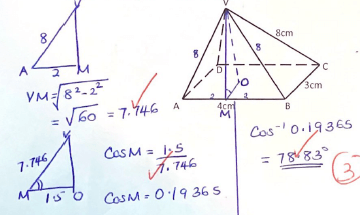
- area scale factor = 60/10 = 6
[x3 4x+3]
determinant x(x + 3) - 12 = x2 + 3x - 12
x2 + 3x - 12 = 6
- 6 = 0
- 18 = 0
+ 6x - 3x - 18 = 0
x(x + 6) -3(x + 6) = 0
(x + 6)(x - 3) = 0
x + 6 = 0 x - 3 = 0
x = -6 x=3 - log105 - 2log1010 +log10(2x + 10) = log10(x - 4)
log105(2x + 10) - log10100 = log10(x - 4)
log10(10x + 50) = log10(x - 4)
100
10x + 50 = x - 4
100 1
10x + 50 = 100(x - 4)
10x + 50 = 100x -400
50 + 400 = 100x - 10x
450/90 = 90x/90
x = 5
√∑(x - 2)2 - [∑(x - a)]x x-60 (x-60)2 71 -11 121 55 -5 25 69 9 81 45 -15 225 65 5 25 57 -3 9 71 11 121 82 22 484 55 -5 25 50 -10 100 20 1216
∑f ∑f
√1216/10 - (20/10)2
= √ 121.6 - 4
= √117.6
= 10.84- (√8)√2
(1 + 1/√2)√2
√16 = 4
√2 + 1 √2 + 1
4 x √2 - 1
√2 + 1 √2 - 1
4√2 - 4
2 - 1
= 4√2 - 4 -
-
- S.A = 2x2 + 4xh
2x2 + 4xh = 24
4xh = 24 - 2x2
h = 24 - 2x2
4x
h = 24/4x - 2x2 /4x
h = a/x - x/2 - v = b.a x h
= x2 x h
= hx2
v = hx2
= x2(6/x - x/2)
v = 6x - x3/2
dv/dx = 6 - 3/2x2
6 - 3x2/2 = 0
12/3 = 3x2/3
√4 = √x2
2 = x
- S.A = 2x2 + 4xh
- M = KDV3
M = K(0.9D)(1.1V)3
M = 0.9 x 1.13 KDV3
M = 1.1979 KDV3
= 1.1979
%change = 1.1979M - M x 100
M
= 0.1979 x 100
= 19.79% - y = x2 - x3
dy/dx = 2x - 3x2
y = x - tx2
dy/dx = 1 - 2tx
= 2(1/3) - 3(1/3)2
= 2/3 - 1/3 = 1/3
= 1 - 2t(1/3)
= 1 - 2/3t
1/3 = 1 - 2/3t
2/3t = 2/3
t = 1 -
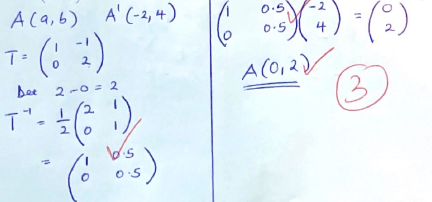
- z = 50º
x = 50 + 25
= 75º - 4x2/4 - 8x/4 + 4y2/4 + 2y/4 = 7/4
x2 - 2x + (-2/2)2 + y2 + (¼)2 = 7/4 + (-2/2)2 + (¼)2
(x - 1)2 + (y + )2 = 7/4 + 1 + 1/16
(x - 1)2 + = 28 + 16 + 1
16
(x - 1)2 + = 45/16
centre(1, -¼) -
Area of ΔABC = ½ x 6 x 5.5 x sin60
= 14.289
14.2894 = ½ x 6 x h
3 3
h = 4.76 ≈ 5cm -
-
- AP: a a+d a+2d
GP: x xr xr2 +
x 3x 9x
a + x = 14
2(a + d + 3x = 34)
a + 2d + 9x = 78
2a + 2d + 6x = 68
a + 2d + 9x = 78
a - 3x = -10
a + x = 14
-4x/-4 = -24/4
x = 6
a + x = 14
a + 6 = 14
a = 8 - 14,34,78
T6 = a + 5d + 35x
a + d + 3x = 34
d = 34 - 26
d = 8
T6 = a + 5d + 243x
= 8 + 5(8) + 243 x 6
= 1506
T5 = a + 4d + 81x
= 8 + 4(8) + 81 x 6
= 526
T4 = a + 3d + 27x
8 + 3(8) + 27 x 6 = 194
+14 + 34 + 78 + 194 + 526 + 1506 = 2352
- AP: a a+d a+2d
- ar = 24
ar2 = 12(x + 1)
r = 12(x + 1) = x + 1
24 2
ar = 24
a(x + 1) = 24
2
a = 24 x 2 = 48
x + 1 x + 1
(48/x+1 + 24 + 12(x + 1) = 76)(x + 1)
48 + 24(x + 1) + 12(x + 1)2 = 76(x + 1)
48 + 24x + 24 + 12(x2 + 2x + 1) = 76x + 76
72 + 24x + 12x2 + 24x + 12 - 76x - 76 = 0
12x2/4 - 28x/4 + 8/4 = 0
3x2 - 7x + 2 = 0
3x2 - 6x - x + 2 = 0
3x(x - 2) -1(x -2)=0
(x - 2)(3x - 1) = 0
x = 2 or x = 1/3
x = 2
-
-
- 4000 + 1100 = 5100 x 12 = 61200
- 4200 x 2 = 8400
3800 x 3 = 11400
4600 x 5 = 23000
= 42800
x + 6 = 18400
x = 18400 = 3066.67
6
12600 + 3066.67 = £15666.67 - 15666.67 x 20 = 26111.11
12
- 10800 = 15311.11 - 26111.11 - 4000 = 22111.11
-
- 4 - x2 = 3x
0 = x2 + 3x - 4
x2+ 4x - x - 4 = 0
x(x + 4) -1(x + 4) = 0
(x + 4)(x - 1) = 0
x = -4 x = 1
y = 3(-4) y = 3(1)
= -12 = 3
Q(-4) P(1,3) -
- 4 - x2 = 0
(2 - x)(2 + x) = 0
x = 2 x = -2
∫-2-4 4 - x2dx = [4x - x3/3]-2-4
(4(-2) - (-2)3) - (4(-4) - (-4)3)
3 3
= -5 1/3 - 51/3
= -10 2/3 = 102/3 -
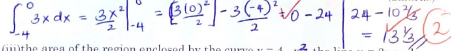
-
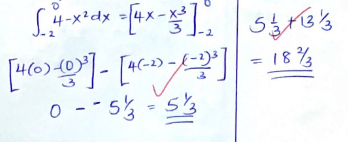
- 4 - x2 = 0
- 4 - x2 = 3x
-
D = S x T
= 800 x 5
= 4000nm
1º = 60cos50º
? = 4000
4000 x 1
60cos50
= 103.7º
k - 45 = 103.7
k = 103.7 + 45
= 148.7ºW- D = Sx T
= 800 x 3/2 = 1200nm
1º = 600m
? = 1200nm
1200 x 1 = 20º
60
x - 50 = 20
x = 70ºN 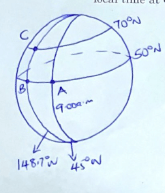
Distance A - B - C
= 4000nm + 1200
= 5200nm
T = D/S
= 5200
800
= 6½hrs
θ = 103.7º
1º = 4min
103.7 = 103.7 x 4 = 414.8
60
= 6hrs55min
9:00
- 6:55
= 02.05am
+ 6:30
8:35am at C
-
-
Marks 31-35 36-40 41-45 46-50 51-55 56-60 No. of candidates 4 6 12 15 8 2 cf 4 10 22 37 45 47 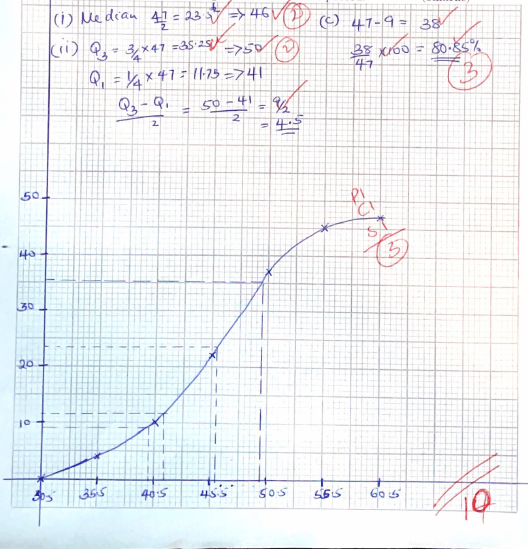
-
-
- 2/5OQ = 2/5q
- q - p
- ¼q + ¾p
-
- OT = h OR
= h(¼q + ¾p)
h/4q + 3h/4 - OT = OP + PT
= p + k (-p + 2/5q)
= p - kp + 2k/5 q
= p(1-k) + 2k/5 q
h/4q + 3h/4p = p(1 - k) + 2k/5 q
3h/4 = 1 - k
4 x h/4 = 2k/5 x 4
h = 8/5k
¾(8/5k) = 1 - k
6/5k + k = 1
11/5k = 1
k = 5/11
h = 8/5
h = 8/11
- OT = h OR
-
Download Mathematics Paper 2 Questions and Answers - Asumbi Girls Mock Examinations 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
