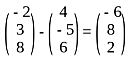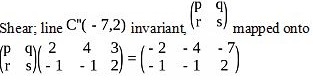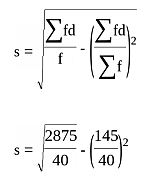Mathematics Paper 2 Questions and Answers - KCSE 2022 Mock Exams Set 2

Questions

Instructions to Candidates

• This paper consists of two sections; Section I and Section II.
• Answer all the questions in Section I and any five questions from Section II
• Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I (50 Marks)
Answer all the questions in this section in the spaces provided below each question

1. A quadratic equation has roots as x=-4 and x=2/3. Write the equation in the form ax2+bx+c=0, where a, b and c are integers. (3 marks)
2. Given that 2≤p≤8 and 3≤q≤10, find the maximum value of: (2 marks)
      p-q   
     q+p
3. Without using a mathematical table or a calculator, write the expression below in the form a3+c, where a and c are constants (3 marks)
                2            
   sin 90° +tan 60°
4. Solve for x in the equation x-3+2=(8-x) (3 marks)
5. A truck is bought at Kshs. 1,800,000. It depreciates by 10% per annum in the first 2 years, thereafter its annual depreciation rate is 15%. Find the value of the truck after 5 years. (4 marks)
6. The position vectors of points A and B are 4i-5j+6k and -2i+3j+8k respectively. Calculate the magnitude of AB correct to 3 decimal places. (3 marks)
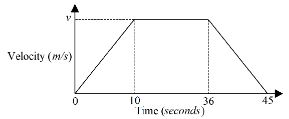
7. The figure below shows the velocity-time graph of a particle that moves for 60 seconds and covered a distance of 852 metres.
   
   Calculate the value of v (2 marks)
8. Make x the subject of the formula: (3 marks)
   px= √(x²+m/Q)
9.    The equation of a circle is x2+y2+6x-10y-2=0. Determine the co-ordinates of the centre and the area of the circle in terms of π (3 marks)
10.      
    1. Expand (1+3x)⁶ in ascending powers of x up to the term in x³ (1 mark)
    2. Use your expansion to evaluate (0.997)⁶ correct to 5 decimal places. (2 marks)
11.  
    1. Complete the table below for the function y=x²-4x+5 for 1≤x≤5 (1 mark)
       

       y	1	1.5	2	2.5	3	3.5	4	4.5	5
       x	2				2		5

    2. Use the mid-ordinate rule with 4 strips to find the area bound by the function, the x-axis and the lines x=1 and x=5. (2 marks)
12. A town T lies on latitude 37°N and longitude 50°E. An airport is located on another town R whose longitude is 100W on the same latitude as T. An aeroplane leaves town T and flies westwards to R. Calculate the distance covered by the plane in km. (Take R = 6370km and π=22/7) (3 marks)
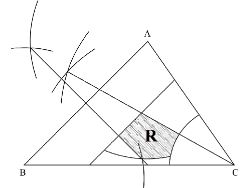
13. The diagram below shows a plot of land. Shade the region R enclosed under the following conditions:
    1. CR≥1.5 cm
    2. R is more than 2 cm from line AB
    3. CRA≥CRB
    4. R is nearer to CB than CA
       
       By construction and using a scale of 1 cm to represent 10 metres, shade the region where the borehole lies. (5 marks)
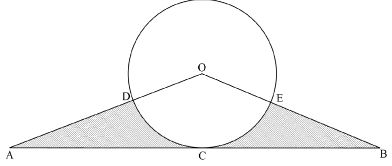
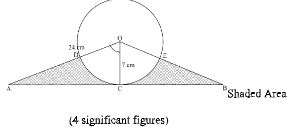
14. In the figure below, O is the centre of the circle. AB is a tangent to the circle at C. AD=17cm and AO=24cm
    
    Calculate the shaded area correct to 4 significant figures. (4 marks)
15. A trader makes two types of chairs; ordinary and special. The cost of each ordinary chair is Kshs. 300 while the cost of a special chair is Kshs. 700. He is prepared to spend not more than Kshs. 21, 000. It is not viable for him to make less than 20 chairs. Ordinary chairs must be less than twice the special chairs but more than 15. By taking the number of ordinary chairs as x and the special chairs as y; Write down all the inequalities representing the above information. (4 marks)
16. A construction firm has two tractors; P and Q. tractor P completes a job in 4 days while tractor Q completes the work in 6 days. The two tractors start working together and after 2 days, tractor P breaks down. How long does it take Q to complete the remaining work? (3 marks)

SECTION II (50 marks)
Answer any five questions in this section

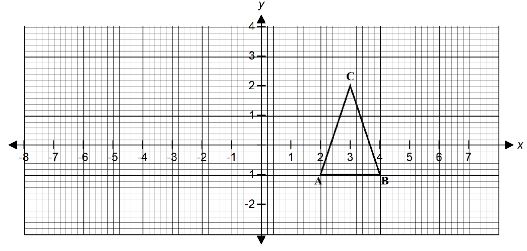
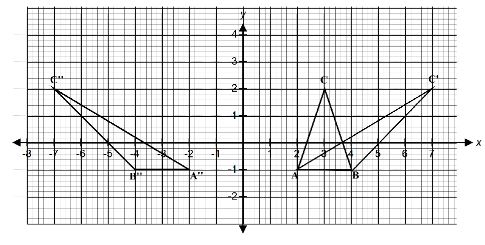
17. The graph below shows a triangle ABC with vertices A2, -1, B(4, -1) and C(3, 2)
    
    1. ΔA'B'C' is the image of ABC under a transformation given by the matrix 1 2 0 1 . Determine the coordinates of A', B' and C' (2 marks)
    2. On the grid provided draw ∆A'B'C' and describe the transformation fully (3 marks)
       
    3. ∆A''B''C'' is the image of ∆A'B'C' under a reflection along the line y=0. Draw ∆A''B''C'' on the same pair of axes and state its coordinates (2 marks)
    4. Determine the matrix representing a single transformation that maps ∆ABC onto ∆ A''B''C'' (3 marks)
18.  
    1. Write down the first three terms of the sequence whose nth term is given by Tn=5n-2 (1 mark)
    2. The third and the sixth terms of a geometric sequence are 18 and 486 respectively. Find the first term and the common ratio of the sequence. (3 marks)
    3. The first and the last terms of an arithmetic progression are 8 and -190 respectively. If the sum of the first n terms of this arithmetic progression is -3094, find the number of terms in the progression (2 marks)
    4. The second, fourth and seventh terms of an arithmetic progression are the first three terms of a geometric progression. Find the common ratio of the geometric progression if the first term of the arithmetic progression is 2 (4 marks)
19.  
    1. Three variables P, Q and R are such that P varies partly as the square of Q and partly inversely as the square root of R. Determine:
       1. The relationship between P, Q and R given that when P=11¹/₃, Q=2 and R=9 and also when P=14.75, Q=5 and R=64 (4 marks)
       2. Q when P=145¹¹/₁₈ and R=1.44 (2 marks)
    2. Four quantities A, B, C and D are such that A varies jointly with B, the square root of C and inversely as the square of D. Find the percentage change in A if B increases by 21%, C decreases by 36% and D increases by 10% (4 marks)
20. A particle moves along a straight line such that its displacement S metres from a given point S=t³-5t²+4 where t is time in seconds. Calculate:
    1. The displacement of the particle at t=5 (2 marks)
    2. The velocity of the particle when t=5 (3 marks)
    3. The values of t when the particle is momentarily at rest (3 marks)
    4. The acceleration of the particle t=2 (2 marks)
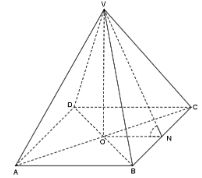
21. The figure below shows a right pyramid standing on a rectangular base ABCD. AB=8 cm, BC=15 cm and each slant edge is 12 cm long. N is the midpoint of BC
    
    Calculate to two decimal places
    1. The vertical height of the pyramid (3 marks)
    2. The volume of the pyramid. (1 mark)
    3. The obtuse angle between the planes VBC and VAD of the pyramid (4 marks)
    4. The angle between line VD and the base (2 marks)
22.  
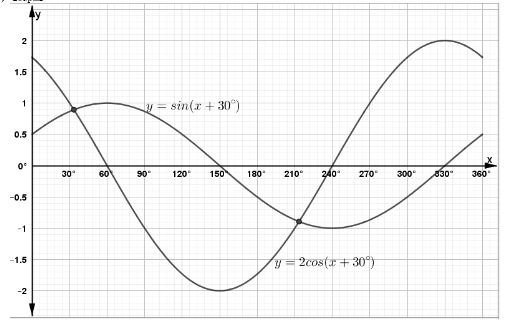
    1. Complete the table below giving the values correct to 2 decimal places. (2 marks)
       

       x	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°	360°
       y= sin (x + 30°)	0.50			0.87		0.00		-0.87			-0.50		0.50
       y= 2 cos (x + 3)	1.73		0.00		-1.73		-1.73		0.00			2.00	1.73

    2. On the same set of axes, draw the graphs of y=sin (x+30°) and y=2cos (x+30°) for 0°≤x≤360°.
       Use the scales x-axis; 1 cm to represent 30° and y-axis; 2 cm to represent 1 unit. (5 marks)
    3. Use you graphs to solve the equation 2cos x+30°-sin (x+30°) =0 (2 marks)
    4. State the amplitude of y=2cos (x+30°) (1 mark)
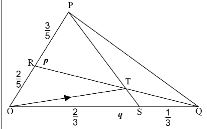
23. A triangle OPQ, R and S are points on OP and OQ respectively, such that OR: RP=2:3 and OS: SQ=2: 1. PS and QR intersect at T. Given that OP=p and OQ = q.
    1. Express in terms p and q
       1. QR (1 mark)
       2. PS (1 mark)
    2. Given that QT=hQR and PT= kPS, express OT in terms of
       1. h,p and q (2 marks)
       2. k,p and q (2 marks)
    3. Find the values of h and k (4 marks)
24. The test scores obtained by 40 students were recorded as shown in the table below
    

    Marks	No. of students
    61 - 65 66 - 70 71 - 75 76 - 80 81 - 85 86 - 90	4 5 9 8 8 6

    
    
    1. Using a working mean of 73, calculate
       1. the mean mark (4 marks)
       2. the standard deviation (3 marks)
    2.  
       1. On the grid provided, draw an ogive to represent the information in the table (3 marks)
       2. Use the ogive to estimate the marks scored by the 25th student. (1 mark)

Marking Scheme

1. x + 4 = 0
   x - 2/3 = 0 → 3x - 2 = 0
   x(3x - 2) + 4(3x - 2)=0
   3x² - 2x + 12x - 8 =0 
   3x² + 10x - 8= 0
   
   
2. max p - min q =   8 - 3   
   min q + min p      3+ 2
        2      
    1 + √3
3.       2(1 - √3)    
   (1 + √3)(1- √3)
   
     2 - 2√3    =    2 - 2√3   = 2 - 2√3 = √3 -1
    1- (√3)²             1-3            -2
   Sin 90°
   
   
4. log₂(8-x) - log₂(x-3) = log₂2²
   Log₂(8-x/x-3)= log24
    8  -  x      = 3
     x - 3 
   4(8 - x) = x -3
   32 - 4x = x -3
   32 + 3 = x + 4x → 5x = 35
   x = 7
   2log₂2
5. 1458000
   Amount = 1458000 (1 - 15/100)3
   895394.25
   AB= OB -  OA =  
   
   
6. |AB| = √(-6)² + 8² + 2²
   √104
   = 10.198 units
   AB = -6i + 8j - 2k
   
   
7. v(71) = 852
   v =852/17 = 24m/s
   (px)² = x² + m/Q
   
   
8. p²x² - x² = m/Q
   x²(p² - 1)= m/Q
   x² = m/Q x 1/p²-1
   x = ± √(m/Q(p²-1))
   x² + 6x + 3² + y² - 10y + (-5)² = 2 + 3² + (-5)²
   
   
9. (x + 3)² + (y -5)² = 36
   (x + 3)² + (y - 5)² = 6²
   →(-3,5)
   Centre 6
   Radius = (x - a)² + (y - b)² = r² units
   (x - a)² + (y - b)² = r²
10.        
    1. Binomial co-effecients
       (1 + 3x)⁶ = 1 + 6(3x) + 15(3x)² + 20(3x)³ + ...
       (1 + 3x)⁶ = 1 + 18x + 135x² + 540x³ + ...
       1 + 3x = 0.0997 → 3x = 0.997 - 1 = -0.003
    2.  x = -0.001
11.       
    

    1	1.5	2	2.5	3	3.5	4	4.5	5	x
    		1.25	1	1.25	2	3.25	5	7.25	10

    =13
    =10° + 50° = 60°
    RT = ⁶⁰/₃₆₀ x 2 x ²²/₇ x 6370Cos37°
    
    
12. Cos θ = 7/24 → Cos-1(7/24)= 73.04°
    Change in longitude 
    AOB = 2 x 73.04° = 146.08°
    Area of ΔAOB = 1/2 x 24 x 24 x sin 146.08°
13.     
    
14.        
    
    = 160.7140cm²
    Area of sector = 146.0/360 x 22/7 x 7x7 = 62.4898cm²
    160.7140 - 62.4898 = 98.2242 = 98.22cm²
    
    
15. Shaded area 300x + 700y < 21,000
    x + y > 20
    x < 2y
    x>15
    P and Q in 1 day → 1/4 + 1/6 = 5/12
    P and Q in 2 days → 2 x 5/12 = 5/6
    
    
16. Remainder = 1 - 5/6 = 1/6
    Q does 1/6 in 1 day
    
    
17.     
    1.   
       
    2. A''B''C''
       
       
       
    3.    
       
    4. Let the matrix be 4p - 2q = -4
       7p = -11 → 11p = -11/7
       T₁ = 5 x 1 - 3 = 3
       T₂ = 5 x 2 - 2 = 8
       T₃ = 5 x 3 - 2 = 13
       T₃ = ar^3-1 = ar² = 18
       T₆ = ar^6-1 = ar⁵ = 486
       
18.        
    1.   ar⁵ = 486
       ar² 18
       r³ = 27
       r = ³√27
       = 3
       
       
    2. - 3094 = n/2(8 + (-190))
       -3094 x 2 (n - 190)
       n =    -3094   x    2 
                  (8 - 190)
       n= 34
       T₂ = a + d , T₄ = a + 3d , T₇ = a + 6d
       
       
    3. Number  of terms
       2 + d , 2 + 3d , 2 + 6d
         2 + 6d =   2 + 3d
       2 + 3d         2 +d
       (2 + 6d)(2 + d) = (2+ 3d)(2 + 3d)
       2(2+d)+ 6d(2 + d)= 2(2 + 3d)+ 3d (2  + 3d)
       
       
    4. 4 + 14d + 6d² = 4 + 12d + 9d²
       14d - 12d = 9d² - 6d²
       2d = 3d² → 2 = 3d
       d= 2/3
       r =       2 + 6 x 2/3         = 3/2 = 1 ½
               2 + 3 x 2/3
       ³√27 = 2/3
       P= kQ2 + c/√R
       11 ¹/₃ = 4k + c/√9 → 34/3 = 4k + c/3 → 34 = 12k + c ...(i)
       14¾ = 5k + c/√64 → 59/4 = 5k + c/8 → 118 = 40k + c ---(ii)
       
       
19.             
    1.     
       1. Relationship
           - 28k = -84
          k =   -84   = 3
                 -28
          12 x 3 + c = 34 → c = 34 - 12 x 3
          c = -2
          P = 3Q² - 2/√R
          P = 145 ¹¹/₁₈
          R= 1.44
          P = 3Q² - 2/√R → 145 ¹¹/₁₈ = 3Q2 - 2/√1.44
          3Q² = 145 ¹¹/₁₈ + 2/1.2
          Hence 
          3Q² = 2651
                     18
       2. Q² = 2651/18 x 1/3 = 2651/54 
          Q = √2651/54 = 7.007
          A_α kB√C → A = kB√C  
                   D²               D²
          B₁ = 1.21B, C1 = √0.64C = 0.8√C
          D₁ = (1.1D)2 = 1.21D2
          A₁ = k (1.21B)0.8√C = 1.21 x 0.8 (kB)√C
                        1.21D²                  1.21D²
          A₁ = 0.8A
          Percentage change in A = 0.8 -1 x 100
                                                        1
    2. A, B , C and D = -20%
       A decrease of 20%
20.             
    1. t(3t - 10)= 0
       t =0
       
       
    2. Velocity at 3t = 10 → t = 3 ¹/₃
       Hence t = 3 ¹/₃
       t = 2
       
       
    3. Time at dv/dt = 6t - 10
       a = 6 x 2 - 10 = 2m/s²
       t= 0
       VN = √(12² - 7.5²)
       
       
    4. VN = √87.75 = 9.367cm at VO = √(9.3672 - 42)  = 8.46998 ≅ 8.47
       Volume = 1/3 x 8 x 15 x 8.47 = 338.80
21.            
    1. Obtuse VMN = 180° - 50.56° = 129.44°
       Sin θ = 8.47/12
       θ  sin-1(8.47/12)= 44.90°
       0° 
    2. Volume of pyramid= 30°
    3. Consider ΔVMN where M is the midpoint o f AD
       60°, 90°, 120°, 150°, 180°
    4. Consider ΔVDO
       210°, 240°
22.          
    1. Table values
       
       

       x	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°	360°
       y= sin (x + 30°)	0.50	0.87	1	0.87	0.87	0.00	-0.5	-0.87	-1.00	-0.87	-0.50	0.00	0.50
       y= 2 cos (x + 3)	1.73	1.00	0.00	-1.00	-1.73	-2.00	-1.73	-1.00	0.00	1.00	1.73	2.00	1.73

       B2 - all table values correct (B1 for at least table values correct)
    2.    
       
       S! - given scales used
       P1 - plotting 
       C1 - drawing 
       P1 - plotting
       C1 - drawing 
       
       
23.        
       
    1.      
       1. QR = QO + OR
          QR = -q + ²/₅p 
       2. PS = PO + OS 
          PS= -p + ²/₃q  
    2. QT = hQR → QT = h(-q + ²/₅ p)
       QT = ^2h/₅ p - hq
       PT = kPS → PT = k (-p + ²/₃q)
       PT = ^2k/₃ q - kp
       
       1. OT = OQ + QT = q - hq + ^2h/₅ p 
          OT = (1-h)q + ^2h/₅ p
          OT = OP + PT → p - kp + ^2k/₃ q
          OT = (1-k)p + ^2k/₃q
    3. h and 2h/5 = 1 - k → 2h + 5k = 5 ...(i) x 3
       1 - h = 2k/3 → 3h + 2k = 3...(ii) x 2     
       6h + 15k = 15
       6j + 4k = 6
       11k = 9 → k = 9/11
       2h + 5 x 9/11 = 5
       2h = 5 - 45/11
       2h = 10/11 → h = 10/11 ÷ 2 = 5/11
       k = 9/11
       h = 5/11
24.           
    1. d = x-A
       

       classes	f	d		d2	fd2	cf
       61 - 65	4	10	63	100	400	4	65.5
       66 - 70	5	5	68	25	125	9	70.5
       71 - 75	9	0	73	0	0	18	75.5
       76 - 80	8	5	78	25	200	26	80.5
       81 - 85	8	10	83	100	800	34	85.5
       86 - 90	6	15	88	225	1350	40	90.5
       	40				2875

         
       
       1. Mean  (x) = A + Σfd/Σf = 73 + 145/40 - M1
          Mean= 76.625
       2. Standard deviation 
          
          s= 7.664
    2.    
       1.  student should draw curve
       2. Student should be able to estimate.