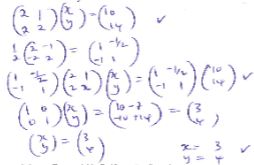Mathematics Paper 2 Questions and Answers - Moi Tea Mock Examinations 2022

Questions

INSTRUCTIONS TO CANDIDATES:

• This paper contains TWO sections: Section I and Section II.
• Answer ALL the questions in Section I and FIVE questions from section II.
• All answers and working MUSTbe written on the question paper in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I

1. Use logarithm table to evaluate (4marks)
   5√(75.4 x 4.83²/ 0.00521)
2. Make b the subject of the formula given that (3 marks)
   a =         bd      
            Nb² - d
3. Line PQ is the diameter of a circle such that the coordinates of P and Q are (-2, 2) and (-2,-6) respectively. Find the equation of the circle in the form . (4marks)
   ax² + ay² + bx + cy + d = 0
4. Use completing the square method to solve the equation
   4 - 3x - 2x² = 0 (3marks)
5. Given that P=4+2 and Q=2+2 and thatPQ=a+bc , where a, b and c are constants, find the values of a, b and c. (3 marks)
6. The table below shows the temperature readings of four different solutions recorded by students to nearest during a laboratory lesson. Calculate the percentage error in ^P+Q/_{S - R} to 3 d.p. (3marks)
   

   Quantity	Temperature in
   P	22.5
   Q	19.4
   R	17.3
   S	26.2

7. Use matrix method to solve the simultaneous equations (3marks)
   2x + y =10
   2x +2y =14
8.      
   1. Expand (1+2x)⁵ to the fourth term. (1 mark)
   2. Hence evaluate (1.02)⁵ correct to 3 decimal places. (3 marks)
9. . It is known that the value of land appreciate at 7% p.a in a town. John bought a plot in the town at Ksh 500,000. Given that he plans to sell the plot after 6 years, find out how much profit he expects to get. (Give your answer correct to the nearest thousand). (3marks)
10. The mass of a wire varies jointly with its length and with the square of its diameter. A section of the wire 500m long, with diameter 3mm has a mass of 31.5kg. what is the mass of 1000m of wire of diameter 2mm? (3marks)
11. Mr. Gatua has a salary of sh.80000 per annum. He lives rent free in company house and is entitled to a monthly personal relief of sh.1056. Based on the tax rates given below, calculate his PAYE. (3 marks)
    

    Taxable income (KE p.a)	Rate
    1 - 1500	10%
    1501 - 3000	15%
    3000 - 4500	25%
    Above 4500	35%

12. The third term and sixth term of a geometric series are 31/3 and 111/4 respectively. Calculate the common ratio and hence find its first term. (3marks)
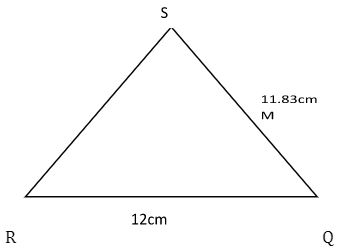
13. Use the figure below to answer the question that follows
    
    Given that angle RSQ = 500, SQ= 11.83 cm and QR=12cm.A circumcirle is drawn on the triangle.Find the radius of the circle (2marks)
14. A Business man bought commodity A and commodity B at shs.60 and sh.72 respectively. In what ratio must he mix so that when he sells at shs.78, he makes a profit of 200%. (3 marks)
15. Points A(x°N,30°E) and B(x°N, 50°E) are 1935 kilometres apart. Taking R= 6370 km and π=²²/₇ , find the value of x. (3marks)
16. Find the gradient function of the curve y= 1/3x³ – 4x² + 9x + 4hence,find the gradient of the curve at point (1,-4) (3marks)
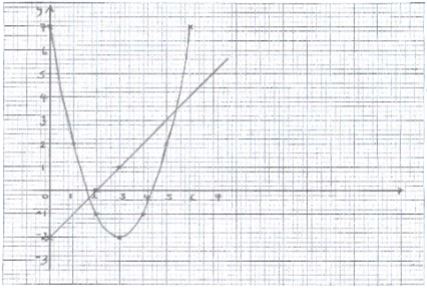
17. Use a scale of 1:1 in both axes to draw the graphs of y = x² – 6x + 7 and y = x – 2 for the domain 0≤ x ≤ 6. The point of intersection of the two functions satisfy a certain quadratic equation in x. Obtain the equation in x hence calculate it’s solutions. Give answer correct to 2d.p. (10 marks)
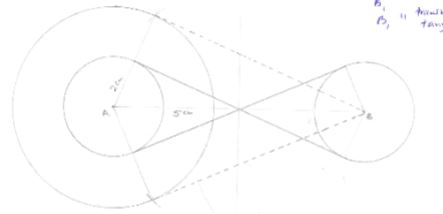
18. Points A and B are centres of two equal circles of a radius 2 cm and 10 cm apart.
    1. Construct the two circles in the space given below. (1mark)
    2. Construct the transverse common tangents to both circles. (4marks)
    3. Calculate the length of the transverse common tangents (Take π=²²/₇  ) (5marks)
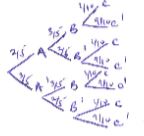
19. Albert, Bonny and Charles competed in a game of chess. Their probabilities of winning the game are 2/5, 3/5 and 1/10 respectively.
    1. Draw a probability tree diagram to show all the possible outcomes.(2 marks)
    2. Calculate the probability that;
       1. No one loses the game. (2 marks)
       2. Only one of them wins the game. (2 marks)
       3. At least one of them wins the game. (2 marks)
       4. At most two of them lost the game. (2marks)
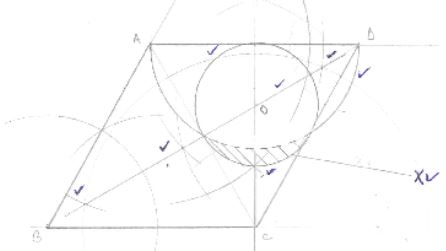
20. Construct rhombus ABCD such that AB=BC= 6cm and ∠ABC=600.
    1. Measure BD. (1 mark)
    2. On the same diagram, construct the inscribed circle of triangle ACD. (3marks)
    3. Construct the locus of points equidistant from A and C. (3 marks)
    4. If x is a point on the circle in b above such that AX=XD and ∠AXD is acute, find the locus of X and make it on the diagram. (3 marks)
21.         
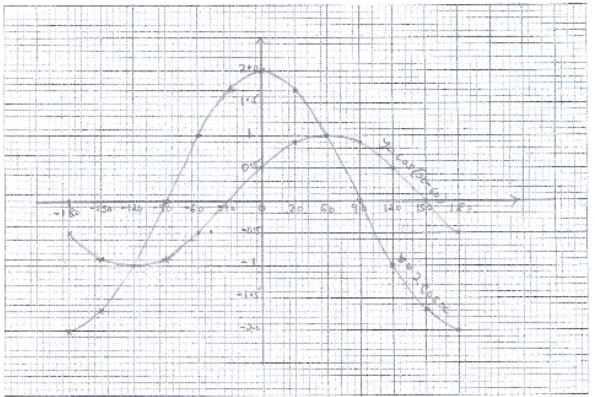
    1. Complete the table below (2marks)
       

       X

       -180°

       -150°

       -120°

       -90°

       -60°

       -30°

       0°

       30°

       60°

       90°

       120°

       150°

       180°

       Y = 2Cos x

       -1.73

       1

       2

       1

       0

       Y= cos(x - 60)

       -0.5

       0.9

       0

       1

       -0.5

    2. On the same axes plot the graphs of y= cos(x-600) and y = 2 cosx (use a scale of 1unit for 300 on the x axis and 1 unit for 0.5 units on the y axis) (4mrks)
    3. Describe the transformation which maps y= cos(x-600) to y = 2cosx. (2marks)
    4. State the period and amplitude of each of the waves above. (1mark)
       

       	Amplitude	Period
       Y = 2Cos x
       Y = Cos(x - 60)

    5. Using the graph above determine the values of x for which
       cos(x-60°) - 2cosx = 0 (1mark)          
22.    
    
    The roof of a building is as shown in the figure above with a rectangular base ABCD. AB = 20m and AD = 8m. The ridge EF = 10m and is centrally placed. The faces ADE and BFC are equilateral triangles. Calculate
    1. The height of E above the base ABCD (2 marks)
    2. The angle between the planes ABCD and ADFE (3 marks)
    3. The angle between the planes AED and ABCD (2 marks)
    4. The acute angle between lines DB and EF (3 marks)
23. Kiprop has at least 50 acres of land on which he plans to plant potatoes and cabbages. Each are of potatoes requires 6 men and each are of cabbages requires 2 men. The farmer has 240men available and he must plant at least 10 acres of potatoes. The profit on potatoes is kshs.1200 per acre. If he plants x acres of potatoes and y acres of cabbages;
    1. Write down 3 in equalities in x and y to describe the information.(2 marks)
    2. Represent these in equalities graphically. (use a scale of 1:10 for both axes) (4 marks)
    3. Use your graph to determine the number of acres for each vegetable which will give maximum profit. (4 marks)
24.             
    1. Complete the table below for y = x² - 3x + 5 in the range 2 < x < 8 (2marks)
       

       x	2	3	4	5	6	7	8
       y	3		9		23	33

    2. Use the trapezium rule with six strips to estimate the area enclosed by the curve , x- axis and the lines x=2 and x=8 (2 marks)
    3. Find the exact area of the region given in (b) (4 marks)
    4. Calculate the percentage error in the area. (2marks)

Marking Scheme

1. 
   

   No	Log
   75.4 4.83	1.8774 0.6839
   4.83	2.5613 0.6839
   0.00521	3.2452 3.7168
   	5.5284/5
   1.276 x 101	1.1057
   12.95

2. a² =     b²d²       
            Nb² - d
   Nb²a² - a²d = b²d²
   Nb²a² - b²d² = a²d
   b² (Na² - d²)= a²d
   b² = a²d
   Na² - d²
   b = ± √a²d/a²N-d
3. (-24 -1/2 , -6+2/2)
   Centre (-2,2)
   radius √(-2,2)² + (2 -6)²
   NO = 16 = √16 = 4 units
   (x + 2)² + (y - 2)² = 16
   x² + 4x + 4 + y² - 4y + 4 = 16
   x² + y² + 4x - 4y + 8 -16 = 0
   x² + y² + 4x - 4y - 8 = 0
4. -2x² - 3x + 4 = 0
   x² + 3/2x - 2 = 0
   x² + 3/2x - 2 = 0
   x² + 3/2 - 2
   x² + 3/2x + 9/16 = 2 + 9/16 = 41/16
   (x + 3/4)² = 41/16
   x + 3/4 = ± √41/4
   x = 0.8508 or -2.3508
5.    4 + √2     x    2 + √2    = 4(2 - √2) + √2(2 - √2)
      2 +√2            2 - √2                  4-2
   8 - 4√2 + 2√2 - 2
               2
   6 - 2√2 =  3 - √2
      2
   a = 3
   b = -1
   c = 2
6. Max    22.55 + 19.45     =   105    = 4.77
             26.15 - 17.35             22
   Min    22.45 + 19.35     =    209   = 4.64
           26.25 - 17.25             25 
   Actual    22.5 + 19.4       = 419 = 4.71
                 26.20 - 17.30
   4.77 - 4.65 
        2                           x 100
        4.71
   11/200 ÷ 4.7 x 100 = 1.168 %
7.    
   
8.        
   1.     
      1 + 5 (22) + 10(2x)2 + 10(2x)3 
      1 + 10x + 40x2 + 80x3
   2. (1.02)5 : (1 + 0.02)5
      2x = 0.02
      x = 0.01
      1 + 10 x 0.01 + 40x (0.01)2 + 80 x (0.01)2
      1 + 0.1 + 0.004 + 0.00008
      1.10408
9.   L = P (1 + r/100)n
   500,000 (1 + 0.07)6
   500,000 (1.07)6
   750,365.1759
   750, 365.1759 - 500,000
   250,365.1759 ≈ 250,000
10. Mass → M 
    Length → diameter
    M = kld² where 1l is a constant
    31.5 =     300 x 3x 3k
    
    k =     31.5       = 7/1000
            500 x 9
    M = 7/1000 x 1000 x 2 x 2
    = 28kg
11. 80,000 x 1.15   = 4600
       20 
    (150 + 225 + 375 + 35) x 20 = 1308.33
                      12
    1308.33 - 105.6
    = 252.33
    ≈ 252
12. ar² = ¹⁰/₃
    ar⁵ = ⁴⁵/₄
    a = ¹⁰/₃ / r²
    a = ⁴⁵/₄ / r⁵
    10/3 x 1/r² = 45/4 x 1/r⁵
    10/3r² = 45/4r5
    40r⁵ = 135r²
    r3 = 135/40
    r = 3/2
    a x 9/4 = 10/3
    a = 40/27
13. a/SinA = b/Sin B= c/SinC = 2R
    12?Sin 30 = 2R
    R=     12     
          2Sin 300
    =7.8324
14. 60A + 72B = 68
       A+B
    60A + 72B = 68A + 68B
    -8A = -4B
    A/B = 4/8 = 1/2
    A:B = 1:2
15. 20/360 x 22/7 x 2 6370Cos s = 1935
    Cos x =    1935 x 7 x 360        = 0.8699
                   20 x 22 x 2 x 6370
    x = Cos^-1 0.8699
    = 29.55
16. dy/dx = x2 - 8x + 9
    (1)2 - 8(1) + 9
    1 + 9 - 8 = 2
17.  
    
    x2 - 6x + 7 = x -2
    x2 - 7x + 9 = 0
    x = 7 ± √49 - 4x 1 x 9
                    2
    x = 7 ± √13
             2
    x = 5.30 or x 1.70
18.    
    
    Length of belt
    √52 - 22 = √21 = 4.5826
    Cos-1 2/5 = 66.42°
    180 - 66.42 = 113.58
    113.58 x 2 = 227.16
    2(22.7/360 x 22/7 x 4) + (4.5826 x 4)
    15.85 + 18.33
    34.18
19.       
    1.      
       
    2.        
       1.   2/5 x 3/15 x 1/10
          3/125
       2. 2/5 x 2/5 x 9/10 or 3/5 x 3/5 x 9/10 or 3/5 x 2/5 x 1/10
          18/125 + 81/250 + 3/125
          = 125/250
       3. 1 - (3/5 x 2/5 x 7/10)
          1 - 27/125
          = 98/125
       4. 1 - 123/250
          127/250
20.               
    1.  11.3cm
    2.       
       
21.             
    1.    
          

       X	-180°	-150°	-120°	-90°	-60°	-30°	0°	30°	60°	90°	120°	150°	180°
       Y = 2Cos x	-2	-1.73	-1	0	1	1.73	2	1.73	1	0	-1	-1.73	-2
       Y= cos(x - 60)	-0.5	-0.7	-1	0.9	-0.5	0	0.5	0.9	1	0.9	0.5	0	-0.5

    2.     
       
    3.  Translation by translation vector (-60) followed by a stretch , stretch 2  x- axis invariant
    4.    
        

       	Amplitude	Period
       Y = 2Cos x	2	360 °
       Y = Cos(x - 60)	1	360°

    5.    x= -120° and 60°   
22.               
    1. Height √48 - 25
       √23 = 4.7958
    2. tan θ = √23/15
       θ tan^-1 = √23/15 = 17.73°
    3. Cos θ = 5/√48
       θ = Cos-1 5/5/√48 = 43.81
    4. α = Tan-1 4/15 = 14.93°
23.            
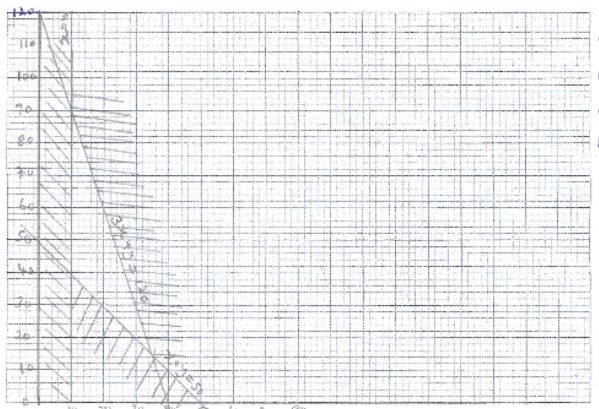
    1. x + y > 50
       x > 10
       3x + y < 120
    2.   
       
    3. (10, 90)
       118000
24.           
    1.      
          

       x	2	3	4	5	6	7	8
       y	3	5	9	15	23	33	45

         
    2. h = 8 - 2 = 1
                6
       1/2 x 1 {(3 + 45 ) + 2 (5 + 9 + 15 + 23 + 33)}
       1/2 {48 + 170}
       1/2 {218}
       = 109
    3. ⁸₂∫(x² - 3x + 5)dx = [x³/3 - 3x²/2 + 5x + c]⁸₂
       [⁵¹²/₃ - ¹⁹²/₂ + 40 + c] - [⁸/₃ - ¹²/₂ + 10 + c]
       108 sq units
    4. 109 - 108 = 1
       1/108 x 100
       = 0.9259%