Physics Paper 3 Questions and Answers - Kakamega Evaluation Mock Exams 2022

QUESTIONS

1. Question 1
   PART A
   You are provided with the following:
   Metre rule
   Vernier Callipers.
   300g mass
   Two knife edges.
   Thread
   Proceed as follows:
   1. Place the metre rule on the knife edges such that each is 5cm from the end.
      Ensure the mm scale is facing upwards. Set the distance between the knife edges,
      L= 900mm.
   2. Place the vernier callipers vertically against the metre rule at 50cm mark with thedepth gauge lowered to touch the bench.
      1. Record the height ho of the upper edge of the metre rule at the 50cm mark
         ho = _______cm _______mm (1mark)
      2. Using the thread provided hang the 300g mass at 50cm mark of the metre rule ensuring it does not touch the bench. Measure and record the height h of the upper edge of the metre rule from the bench at the 50cm mark.
         h = _______cm _______mm (1mark)
      3. With the 300g mass hanging at the 50cm mark, adjust the position of the knife edges so that the distance L is 600mm with the knife edges equidistant from the 50cm mark i.e. at 20cm from each end.
         Measure and record the height h of the upper edge of the metre rule at 50cm mark.
         h = _______cm _______mm (1mark)
         Table
         

         Length L(mm)	900	600
         Height h(mm)
         Depression, d = (ho-h) (mm)
         Log L
         Log d

         (3marks)
   3. Determine the value of s = log 900 - log600  (2marks)
                                                 logd₉₀₀ -log d₆₀₀
   4. Evaluate y= ¹/_s (1mark)
   5. Given that G= ^{log K}/_y where G=2.75, determine the value of K. (1mark)
      PART B
      You are provided with the following:
      A white screen with crosswires
      A Mounted lens
      A White screen
      A Candle
      A Metre rule
      Proceed as follows:
   6. Estimate the focal length of the lens by focusing the image of a distant object on the screen provided e.g. distant window.
      fo = ___________cm (1mark)
   7. Arrange the apparatus as shown.
      
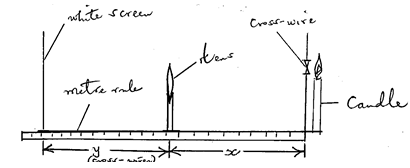
      With the object (cross-wires) illuminated using a candle flame placed at x=15cm, move the screen until a sharp magnified image of the object is formed on the screen.
      Measure and record the corresponding value of y in the table.
   8. Repeat step (g) for the value of x=18 cm
      Table (3 marks)
      

      x (cm)	15	18
      y (cm)
      x+y(cm-1)  xy

   9. Determine the average of ^x+y/_xy (2marks)
   10. Compare the average ^x+y/_xy and ¹/_fo (2marks)
   11. Given that ¹/_fo = ^y/_(^y/x)+1 and x=25 cm.Determine the value of y. (2marks)
2. Question 2
   PART A
   You are provided with the following:
   A voltmeter
   A resistance wire labelled R mounted on a metre rule.
   A metre rule.
   A resistance wire labelled T mounted on a small piece of carton.
   Two dry cells and a cell holder.
   Six connecting wires, each with a crocodile clip at one end.
   A switch.
   Proceed as follows:
   
   1. Measure and record the e.m.f. E0 of the cells connected in series, E₀ = ____ V.(1mark)
   2. Connect the circuit as shown below. Point O on the resistance wire R is at 50cm mark of the metre rule. A and B are points on resistance wire R such that AO = OB = x = 30cm.
      
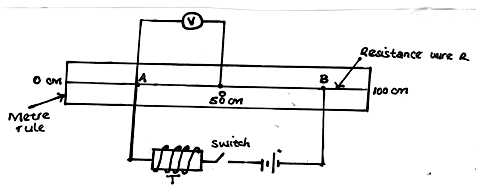
   3. Close the switch. Read and record the potential difference V across AO
      V = …………………………………………. Volts. (1mark)
   4. The relationship between V and x is given by:
      ¹/_V = ³⁵/_x + ¹/_y
      Determine the value of y. (2marks)
   5. Use the e.m.f. E0 to determine the constant k, given that:
      k = ⁸/_35E0 
      PART B
      You are provided with the following:-
      A glass beaker
      A Bunsen burner
      A Thermometer
      A Stop watch
      A Tripod stand and a Wire gauze
      A measuring cylinder
      Water in a container
      Proceed as follows:
   6. Set the apparatus as shown in the figure.
      
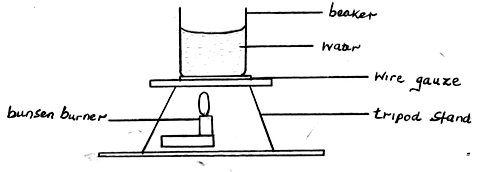
   7. Measure 100cm³ of water and pour it into the beaker. Take the initial temperature of the water.
      T₀ = …………………………………………….ºC (1mark)
   8. Now heat the water to a temperature of 80ºC. Switch off the gas tap and place a thermometer into the beaker and start the stop watch when the temperature is 65ºC. Take the temperature T (ºC) of water after every two minutes. Record your results in the table
      Table (5marks)
      

      Time, t(min)	2	4	6	8	10	12	14
      Temperature , T ( ºC)
      (T - T0) (ºC)
      Log (T - T0)

   9. Plot a graph of Log (T - T0) against Time (t). (5marks)
   10. Determine the value of P (log (T - T0)) when t = 0. (1mark)
   11. Determine N, where N is the antilog of P. (1mark)
   12. Determine the temperature of the surrounding TR using the expression
       N = 65–T_R (2marks)

CONFIDENTIAL
Each candidate is required to have the following:
QUESTION 1

• A candle
• A white screen
• A lens and a convex lens holder. NB: Focal length = 20cm.
• A metre rule.
• A white screen with crosswire
• A Vernier Callipers.
• A 300g mass
• Two knife edges.
• Thread 15cm long

QUESTION 2

• A stop watch
• A 250ml glass beaker
• A thermometer (-10 to 110ºC)
• A tripod stand and wire gauze
• A measuring cylinder 100ml
• A source of heat
• Some water in a container about 500ml at room temperature
• A voltmeter (0 – 5V)
• Two new dry cells and cell holders
• Six connecting wires, each with a crocodile clip at one end.
• A switch.
• Tissue paper
• A resistance wire labelled R mounted on a metre rule.
  The physics teacher is required to mount a nichrome wire SWG 28 on a metre rule and label the wire R. The diameter of the wire is 0.36mm.
• A resistance wire labelled T.
  The Physics teacher is required to mount a nichrome wire SWG 28 on a small piece of carton box and label it T.
  The diameter of the wire is 0.36mm and its length is 60cm.

MARKING SCHEME

QN 1

2.        
   1. h_o = 92.00cm = 920.0mm
   2. h = 83.00cm = 830.0mm
   3. h = 90.00cm = 900.0mm
      • Candidate’s own correct evaluation for both values of depression, d = (h_o-h)(mm) 1mk
      • Log L 2.954 2.778; both values correct 1mk
      • Candidate’s own correct evaluation for both values of log d 1mk
3. Correct substitution 1mk
   Correct evaluation to at least 4s.f or exact. 1mk
4. Correct substitution of s ½ mk
   Correct evaluation to at least 4s.f or exact. ½ mk
5. Correct substitution of G and y ½ mk
   Correct evaluation to at least 4s.f or exact. ½ mk
6. fo = 20.0 ± 1.0cm 1mk
7. According to fo used by candidates in the centre to 1d.p 2mks
   Candidate’s own correct evaluation of both values of (x+y)/xy 1mk
8. Principle of averaging 1mk
   Correct evaluation to at least 4s.f or exact. 1 mk
9. Correct evaluation of 1/fo 1mk
   They are equal 1 mk /almost equal
10. Correct substitution of 1/fo and x 1mk
    Correct evaluation to at least 4s.f or exact. 1mk

QN 2

1. Eo = 3.1 ± 0.1V 1mk
2. V = 0.4 ± 0.1V 1mk
3. Correct substitution V and x 1mk
   Correct evaluation to at least 4s.f or exact. 1mk
4. Correct substitution of Eo ½ mk
   Correct evaluation of k to at least 4s.f or exact. ½ mk
5. To = 22 – 30 °C 1mk
   

   Time, t(min)	2	4	6	8	10	12	14
   Temperature , T ( ºC)	61	57	53	51	49	47	45

   • ½ mk for correct value of T max 3 mks.
   • Correct evaluation of all values of T – To to at least 4s.f or exact. 1mk
   • Correct evaluation of all values of log (T – To) to at least 4s.f or exact.1mk
6.      
   • Correct labeling of axes:
     Log (T – To) ONLY on y-axis
     Time, t (min) on x-axis A1
   • uniform and simple scale S1
   • plotting exact or within one small square ½ mk to max P2. Repeated value treated as one.
   • Straight line (drawn using a straight edge) with a negative gradient passing through at least 3 correctly plotted points. L1
7. P= y-intercept. evidence from graph ½ mk
   correct reading ½ mk
8. Correct reading of antilog 1 mk
9. Correct substitution of N. 1mk
   Correct evaluation within the range to at least 4s.f or exact with unit. 22 – 30 °C 1mk
   Penalize ½ mk if unit is missing.
   Penalize 1mk if the unit is incorrect