Mathematics Paper 1 Questions and Answers - Mincks Group of Schools Mock Examinations 2022

INSTRUCTION TO CANDIDATES

1. Write your name and Index number in the spaces provided above.
2. Sign and write the date of examination in the spaces provided above.
3. The paper consists of two sections. Section I and Section II.
4. Answer ALL the questions in Section I and any FIVE questions in Section II.
5. Show all the steps in your calculations, giving your answer at each stage in the spaces provided below each question.
6. Marks may be given for correct working even if the answer is wrong.
7. Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
8. Candidates should answer the questions in English.
9. Candidates must check the question paper to ascertain that all pages are printed as indicated and that no question(s) is/are missing.

FOR EXAMINER’S USE
SECTION I

SECTION II

QUESTIONS

SECTION 1 (50 MARKS)
ANSWER ALL QUESTIONS

1. Simplify (4mks)
   
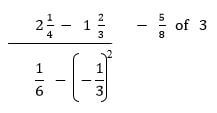
2. Without using table or calculator evaluate. (3mks)
   
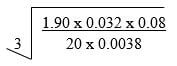
3. The sum of the interior angles of a regular polygon is 40 times the size of the exterior angle.
   Find the number of sides of the polygon. (3mks)
4. A farmer has a piece of land measuring 840M×396M. He divides it into square plots of equal size.
   Find the maximum area of one plot. (3mks)
5. A Kenyan business woman bought goods from Japan worth 2,950,000 yens. On arrival in Kenya the custom duty of 20%was charged on the value of goods. If the exchange rates were as follows:
   1 US dollar =118 yens
   1 US dollar = Sh76
   Calculate the duty paid in Kenya Shilling (3mks)
6. Determine the values of X that satisfy the inequalities and show the solution on a number line. (3mks)
   -3 – x ≤ ⅓ x – 5 > ⅔ x - 6
7. Solve for x in 27^(x+1) -3 ^(3x+2) – 400 =86 (3mks)
8. A business man bought two bags of maize at the same price. On arrival at his business premises he discovered that one was of higher quality than the other. He sold the higher quality bag of maize at Sh. 1,040 and made a profit. He made a loss by selling the low quality bag of maize at Sh. 880. Given that the profit is three times the loss, calculate the buying price. (3mks)
9. The figure below shows triangle PQR in which PR=12cm. T is a point on PR such that TR=4cm. Line ST is parallel to QR.
   
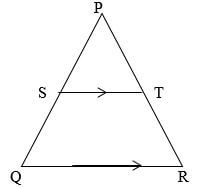
   If the area of triangle PQR is 336 cm2, find the area of the quadrilateral QRTS. (3mks)
10. Two buses A and B leaves the same station. Bus A heads due East while bus B heads due North. The North bound bus travelled at 10km/h faster than the East bound bus. After 5 hours the two busses were 250km apart. Calculate the speed of north bound bus. (4mks)
11. Given that tan x = 12/5, Find the value of (3mks)
    Sin x +2 Cos x, without using a calculator or mathematical table.
        1 – sin x
12. Use reciprocal tables to find the value of 1/0.325
    Hence evaluate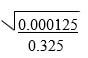  (3mks)
13. Simplify completely (3mks)
    
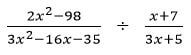
14. Fatuma is now three times as old as her brother and four times as old as her son. Eight years from now, Fatuma age will be twelve years more than the sum of the age of the brother and the son. Find Fatuma’s present age. (3mks)
15. Express 3.5 ̇ in the form of a b/c where a, b and c are constants. (3mks)
16. The diagram below shows a histogram showing marks scored in a certain test.
    
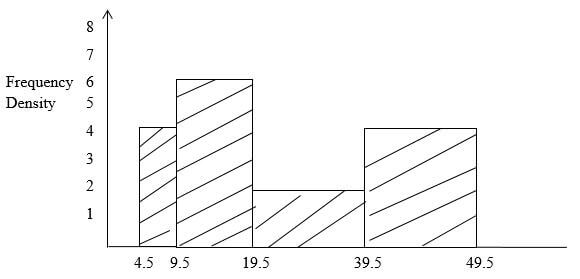
    Develop a frequency distribution table for the data if the first class has a frequency of 8. (3mks) 

SECTION II (50 MARKS)
Answer any five questions from this section.

17. Co-ordinate’s of point P and Q are (1,-2) and (3,10) respectively. Point T divides PQ in the ratio 1:1.
    1. Determine the co-ordinates of T. (2mks)
    2.                  
       1. find the gradient of the perpendicular to PQ. (1mk)
       2. determine the equation of the line perpendicular to PQ and passing through T. (2mks)
    3. Given that the line in (ii) above cuts the Y-axis at point R, calculate the distance TR correct to 4 s.f. (3mks)
    4. Given that point Q is the image of P under a translation, find the image of R under the same translation. (2mks)
18. The model of tank consists of a conical top mounted on a cylindrical part and a bottom hemispherical part. The total height of the model is 15cm, the height of the cylindrical part is 8cm and the radii of hemisphere of the cone is 3cm. (use π =3.142)
    1. Calculate the surface area of ;
       1. The conical part correct to (4 s.f) (2mks)
       2. The cylindrical part correct to (2 d.p) (2mks)
       3. The hemispherical bottom correct to (2 d.p) (2mks)
       4. Total surface area of the model (1mk)
    2. The actual tank has a total height of 6M. find the total surface area of the actual tank. (3mks)
19. There are two sweets manufacturing factories A and B. factory A produces sweets with 60.5% sugar while factory B produces sweets with 80.5% sugar.
    1. Determine the total mass of sugar in 80 kg of sweets from A and 40kg of sweets from B. (3mks)
    2. 80 kg of sweets from A were crushed together with 40kg of sweets from B. find the percentage of sugar in the mixture correct to 2 d.p. (2mks)
    3. Type A sweets cost sh. 37 per kg while type B sweets cost sh. 55 per kg. in what ratio should they mix type A and type B in order to give a profit of 25% when sold at sh. 50 per kg. (3mks)
    4. Find the profit realized after selling 20kg of the mixture. (2mks)
20. The equation of a curve is y=3x³-4x²+1
    Determine;
    1. The gradient function of the curve (1mk)
    2. Find the gradient of the curve when X=1 (2mks)
    3. The equation of the tangent to the curve at the point. (2,3) (3mks)
    4. The angle which the targent to the curve at (2,3) makes with X-axis correct to 1 d.p. (1mk)
    5. The equation of the line L which passes through the point (2,3) and is perpendicular to the targent. (3mks)
21. Triangle ABC with vertices A(3,4) B(1,3) and C(2,1) has the image A¹B¹C¹ with vertices A¹ (-4,3)B¹ (-3,1) and C¹ (-1,2) under transformation T.
    1. Draw triangle ABC andA¹B¹C¹ on the same axes. (2mks)
       
    2. Describe transformation T fully. (2mks)
    3. Draw triangle A¹¹B¹¹C¹¹ the image of A¹B¹C¹ under reflection in the line y=0. (2mks)
    4. Describe a transformation that maps ABC into A¹¹B¹¹C¹¹. (2mks)
    5. Identify two pairs of triangles which are oppositely congruent to each other. (2mks)
22. The diagram below shows two towers AB and CD on a level ground. P and Q are two points on a straight road BD.
    
    
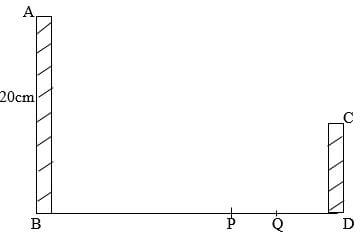
    1. A car moves from B towards D. At point p, the angle of elevation of point A was 11.3°. calculate the distance BP correct to 1dp. (2mks)
    2. The car moving at 36km/h took 5 seconds to move from P to Q.
       1. Calculate distance PQ. (1mk)
       2. Calculate the angle of elevation of point A from Q correct to 1 d.p. (2mks)
    3. Given that QC=50.9M and BD = 200M
       1. Find the height CD correct to 2d.p. (2mks)
       2. Find the angle of elevation of A from C. (3mks)
23. The table below shows height of 50 students.
    

    Height (cm)	140≤×˂145	145≤×˂150	150≤×˂155	155≤×˂160	160≤×˂165
    Frequency	3	15	19	X	2

    1. Find the value of x (1mk)
    2. State the modal class (1mk)
    3. State the modal frequency (1mk)
    4. Estimate the mean height (3mks)
    5. State the median class (1mk)
    6. Estimate the median height (3mks)
24. The figure below shows a circle centre O and radius 17cm. given that QS is the diameter and the rectangle PQRS is inscribed in the circle.
    
    
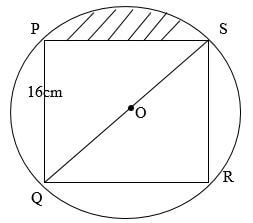
    1. Calculate length PS (3mks)
    2. Calculate angle POS correct to 1 d.p. (3mks)
    3. Calculate the area of the shaded part. (4mks)

MARKING SCHEME

1.  
   9/4 – 5/3 = 27-20   =  7/12
    1/6 -  1/9  = 3-2  =  1/18                   
                        18           
   7/12 × 18/2  = 21/2
   21/2 - 15/8 = 84-15
                            8
   =  69/8 
    = 8 5/8

2. 3√(1.9 × 0.032 × 0.08) × 1000000
            20 × 0.0038         × 1000000
   = 3 √19×32×8
            20×38
   = 3 √     64      
              1000
   =3 √ 4³
         10³
   = 4/10
   = 2/5

3. (2n – 4 ) 90 = (360/n) 40
   180n² – 360n – 14400=0
   n² - 2n - 80 = 0
   n=2   ±  √324
           2
   n= 10 

4. 840= 2³ × 3× 5× 7
   396= 2² ×3²×11

   GCD = 2² × 3 = 12
   Area = 12 ×12 =144 M²

5.  20 × 2950000
   100
   = 590,000 yen
   590,000
       118
   = 5000 dollars
   76 × 5000
   = sh. 380,000
6. -9-3X ≤ X-15
   6 ≤ 4X
   1.5 ≤ X
   X–15 > 2X-18
   3>X
   1.5 ≤ × ˂ 3
   
   

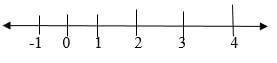
7. 3^3(x+1) – 3^3X+2 = 486
   3^3X × 3³ – 3^3X × 3² = 486
   3^2X (27-9) = 486
   3^3X = 3³
   3X = 3
   X= 1

8. 8. Let loss be X
   Profit = 3X
   1040-3X=880 +X
   1040 – 880 = 3X+X
   160=4X
   X=40
   Buying price = 880+40 = 920

9. 12/8 = 3/2
   ASF = 9/4
   Area PST = 4/9 ×336 = 149 1/3
   Area QRST = 336-149⅓
   = 186 ⅔ cm²

10.          
    
    

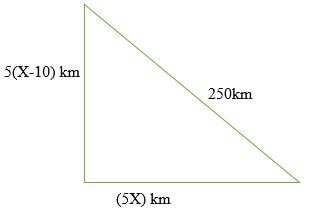
    (5X)² + (5X+50)² = 250²
    25X²+500X-60000=0
    X²+10X-1200=0
    X² + 40X – 30X - 1200 = 0
    X(X+40) – 30 (X+40)=0
    (X-30) (X+40) =0
    X=30
    30+10 = 40Kmh^-1

11. Sin X + 2 cos X
         1-Sin X
    Tan X = 12/5
    12/13 + 2 (5/13) = 22/13
    1-12/13 = 1/13
    = 22/13 × 13/1
    = 22
12.             1              = 10 × 0.3077
        3.25 × 10^-1  
    = 3.077
    0.000125 = (1.25 ×10-4) ½
    = 1.118
         100
    = 0.01118
    = 3.077 × 0.01118
    = 0.0344

13. 2 (X+7) (X-7) × 3X +5
       (3X+5) (X-7) X+7
    = 2

14. 3X+ 8 = 16+ X + 3/4 X + 12
    5/4X = 20
    X= 16
    

    Fatuma = 3×16
    = 48 yrs.

15. Let r = 3.555……. (i)
    10r = 35.55…….(ii)
    Substract e.g (i) from equation(ii)
    qr = 32
    r = 32/9
    = 3 5/9
16.                         

    Class	Frequency
    5- 9	8
    10 - 19	24
    20-39	16
    40-49	16

17.             

    1. T  1+3  , -2+10
               2        2
       T (2,4)
        
    2.                  
       (i) 10+2  = 12
            3-1        2
       = 6
       Gradient of perpendicular = -1/6
       (ii)  Y – 4 = - 1
             X – 2      6
            6Y – 24 = -X +2
             6Y = -X + 26
             Y= - 1 X + 26
                     6        6
    3.                  
       
18.                         
    1.                     

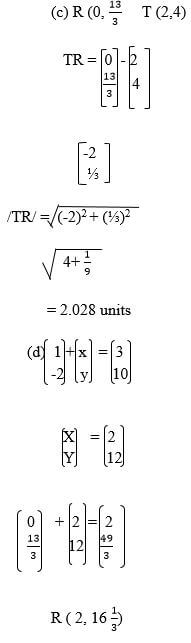
       1. A= ԯrl
          3.142 × 3 ×5
          = 47.13

       2. 3.142 ×6×8
          = 150.82

       3. 2×3.142×3×3
          = 56.56

       4. 47.13 + 150.85 + 56.56
          = 254.51

    2. L.S.F = 15/600 = 5/200 = 1/40

       (L.S.F.)² = (1/40)²
       
       = 1/1600

       254.51 ×1600
       = 407216cm²
       = 40.721m²

19.                        
    1. 60.5/100 × 80  + 80.5/100 × 40 
       48.40 + 32.20
          = 80.6 kg
    2. 80.6/120 × 100
       = 67.17%
    3. 125/100y = 50 
       Y= 40
       
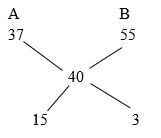
       15: 3
       5:1
    4. (d) (20×50) – (20×40)
       1000 – 800
        = Sh.200
20.                            
    

    1. dy/dx = 9X2 – 8X

    2. Gradient = 9 (1)2- 8(1)
       9-8
       = 1

    3. 9 (2²) – 8 (2)
       36-16
       G=20

       (x,y) (2,3) G=20
       y-3 = 20
       x-2

       y - 3 = 20x – 40
       y = 20x – 37

    4. Tan Ɵ = Gradient
       Tan Ɵ = 20
       Ɵ = 87.1°

    5. Gradient of L =- 1/20

       y-3 = - 1
       x-2    20

       20 y – 60 = -x + 2
       20y = -x + 62
       Y= -1/20x + 62/20

       y= - 1/20x + 3.1

21.                    
    
    1. Plotting ABC
       Plotting A¹B¹C¹
    2. Rotation about 
       (0,0) through + 90°
    3. Location of A¹¹B¹¹C¹¹
       Plotting A¹¹B¹¹C¹¹
    4. Reflection
       Y= -X
    5. ABC and A¹¹B¹¹C¹¹ 
       A¹B¹C¹ and A¹¹B¹¹C¹¹
22.                  
    
    1. Tan 11.3 = 20
                        BP
       BP =    20      
              Tan 11.3
       BP = 100.1 M
    2.                        
       (i)     36000     = 10m/s
                3600    
       Distance = 10×5
       = 50m
       (ii) Tan x = 20/150.1
       Tan X = 0.1332
       X= 7.6°
        
    3. (i) CD = √50.92 – 49.92
       √2590.81 – 2490.01
       √100.8
       = 10.04
       (ii)  Tan y = 9.96
                          200.0
       Tan y = 0.0498
       Y= 2.85°
23.                              
    
    1. 3+15+19+2+x=50
           39 + X = 50
                 X= 11
    2. 150 ≤ × ˂ 155
       150- 154
    3. F= 19
    4.                

       Class	X	Freq	Fx	Cum fre
       140-144	142	3	426	3
       145-149	147	15	2205	18
       150-154	152	19	2888	37
       155-159	157	11	1727	48
       160-164	162	2	324	50
       		∑f=50	∑fx=7570
       			B1	B1

       x- = ∑fx = 7570
               ∑f       50
       = 151.4

    5. Median class = 150 - 154

    6. L+ [N- C.F]  i
             2     F
       149.5 + 7.5/19 × 5
       = 151.47

24.                     
    1. Ps = √342 - 256
       √1156 – 256
       √900
       PS= 30 cm
    2. Sin S = 16/34
       S= 28.1
       28.1 × 2 = 56.2
       180 – 56.2
       POS = 123.8
    3.  
       (123.8/360 × 3.142 × 17 ×17)
       ½ × 17× 17 sin 123.8
       312.26 – 120.08
           = 192.18 cm²