INSTRUCTION TO CANDIDATES
- Write your name and Index number in the spaces provided above.
- Sign and write the date of examination in the spaces provided above.
- The paper consists of two sections. Section I and Section II.
- Answer ALL the questions in Section I and any FIVE questions in Section II.
- Show all the steps in your calculations, giving your answer at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Candidates should answer the questions in English.
- Candidates must check the question paper to ascertain that all pages are printed as indicated and that no question(s) is/are missing.
FOR EXAMINER’S USE
SECTION I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
SECTION II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |
QUESTIONS
SECTION 1 (50 MARKS)
Answer all questions in this section
- Solve the equation 1/3 (2x+1)+1/4 (5x-1)= 1/2 (3mks)
-
- Expand ( 1 – 2x)4 (1mk)
- Use your expansion to find the value of (0.96)4 correct to 4 s.f (2mks)
- The expression 1+x/2 is taken as an approximation for
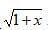 . Find the percentage error in doing so if x = 0.44 (3mks)
. Find the percentage error in doing so if x = 0.44 (3mks) - Solve for x in the equation log8 (x+6) - log8(x-3) = 2/3 (4mks)
- Make p the subject if the formula (3mks)
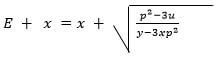
- An auto spare dealer sells two types of lubricants, A and B in his shop. While purchasing, type A cost sh40 per 100ml tin and type be B cost sh.60 per 100ml tin. He has Shs 15,000 to spend on both types of lubricants. Type A should not be less than 3 litres while type B should be atleast a litre . He buys x tins of type A and Y tins of type B. Write down three inequalities which represent the above information. (3mks)
- In the figure below PT is a tangent to the circle at P and AT passes through the centre of the circle.
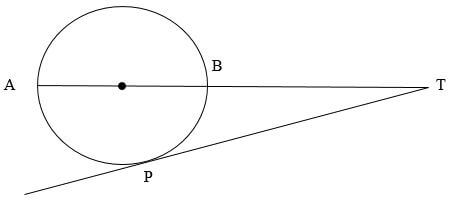
If PT =9cm and AT=12cm, find the- radius of the circle correct to 1 d.p. (3mks) - Find the radius and the centre of the circle whose equation is (3mks)
3x2 + 3y2 – 6x + 3 + 12y = 0 - Without using a calculator or mathematical tables express
 in surd form and simplify (3mks)
in surd form and simplify (3mks) - The table below represents the mass and volume of a liquid measured at room, temperature.
Mass (g)
8
10
20
21
30
37
52
55
70
Volume (cm3)
10
13
20
29
35
43
60
63
70
- By plotting the points and drawing the line of best fit, estimate the density to the liquid. (2mks)

- Determine the equation of your graph. (2mks)
- By plotting the points and drawing the line of best fit, estimate the density to the liquid. (2mks)
- The population of two towns Kathwana and Siakago for three years was as follow.
Calculate the difference in population of the two after six years. (3mks)1st year
2nd year
3rd year
Kathwana
40,000
48,000
56,000
Siakago
40,000
48,000
57,600
- Solve for ∝ in the equation 6 sin2∝ - cos ∝ – 5 = 0 (3mks)
For Ɵ≤ ∝ ≤ 300º - Arabic coffee costing sh90 per kilogram is mixed with rubusta coffee costing sh.75 per kilogram in the ration 2:3. Calculate the selling price of the mixture per kilogram if a profit of 15% if to be realized to the nearest shilling. (3mks)
- The gradient of a curve at any point is given by 2x-1. Given that the curve passes through point (1,5). Find the equation of the curve. (3mks)
-
- Given that AB=6cm. Construct locus of P such that <APB = 90º. (2mks)
- Hence determine the area enclosed by the locus of P. (2mks)
- Given the vectors a = 3j + 2k and b = 4i – 7k
Find p if p = 3a – b (2mks)
SECTION II (50 MARKS)
Answer any five questions from this section
- Three consecutive terms of aGP are (x+2), (x-2), and (x-5). Find:-
- The value of x. (3mks)
- The common ratio (1mk)
- Given that x+2 is the third term of the G.P
Find;- The first term giving your answer as a mixed fraction. (3mks)
- the sum of the first six terms correct to 2 d.p (3mks)
- A form 1 stream at Butere mixed day secondary school has 15 boys and 25 girls. The probability of a girl reaching form 4 is 2/5 and that of a boy is 3/5. If a girl reaches form 4 then probability that she gets employed is 2/3 while the probability that a girl gets employed without reaching form 4 is 1/3. If a boy reaches form 4 the probability that he gets employed is ¾ while the probability that a boy gets employed without reaching form 4 is 1/4
- Draw a tree diagram to illustrate the above information. (2mks)
- Using your tree diagram, determine:-
- the probability that a girl gets employment. (2mks)
- the probability any child who has been to school gets employed. (2mks)
- the probability that a boy fails to get employment. (2mks)
- The probability that anybody who has studied upto form 4 fails to get employment. (2mks)
- The diagram below shows a right pyramid VPQRS with V as the vertex and rectangular base PQRS. PQ=3cm, QR=4cm and the height of the pyramids is 6cm. M and N are the mid-points of PQ and QR respectively.
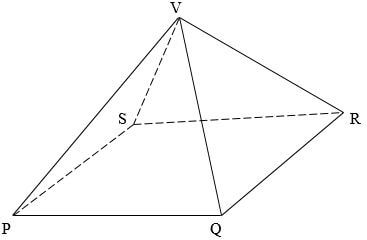
- Calculate
- the length PV (3mks)
- the angle between face VPQ and the base PQRS (2mks)
-
- the slant height VM and VN. (2mks)
- the surface area of the pyramid. (3mks)
- Calculate
- Two towns A and B lie on the same parallel of latitude 60ºN. If the longitude of A and B are 42ºW and 29ºE respectively.
- Find the distance between A and B in nautical miles along the parallel of latitude. (2mks)
- Find the local time at A if at B is 1.00.p.m. (2mks)
- Find the distance between A and B in kilometre (Take π=22/7 and R=6370km) (2mks)
- if C is another town due south of A and 1001km away from A, find the co-ordinate of C. (4mks)
- The table below shows marks scored by students in a mathematics test.
Marks
30-39
40-49
50-59
60-69
70-79
80-89
90-99
No of students
2
3
8
12
15
6
4
- Draw a cumulative frequency curve to represent the information. (4mks)

- Use you graph to find:-
- The median mark (1mk)
- The quartile deviation (3mks)
- the pass mark if 60% of the students passed. (2mks)
- Draw a cumulative frequency curve to represent the information. (4mks)
- The initial velocity of a particle was 1m/s and it acceleration is given by (2-t) m/s2 every second after the start.
-
- Determine the equation representing its velocity. (2mks)
- Find the velocity of the particle during the third second. (2mks)
-
- Find the equation representing its distance t seconds after the start. (2mks)
- What was the distance covered by the particle during the first three seconds. (2mks)
- Determine the time when the particle was momentarily at rest. (2mks)
-
-
- using trapezoidal rule estimate the area bounded by the curve y=3x2 – 2 and the lines x = -4, x=4 and x-axis using 8 trapezia (2mks)
- Find the actual area bounded by the curve y=3x2 -2 and the lines x= -4, x=4 and x-axis. (3mks)
- Calculate the percentage error when trapezoidal rule is used. (3mks)
- The vertices of triangle PQR are P(1,1), Q(4,1) and R(5,4). A transformation represented by a matrix
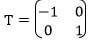 maps triangle PQR onto triangle PIQIRI.
maps triangle PQR onto triangle PIQIRI.
A second transformation represented by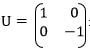 maps triangle PIQIRI onto triangle PIIQIIRII
maps triangle PIQIRI onto triangle PIIQIIRII- On the same axis draw the three triangles PQR, PIQIRI and PIIQIIRII and state the co-ordinated of triangle PIQIRI and PIIQIIRII . (6mks)

- Describe a single transformation which maps triangle PQR onto triangle PIIQIIRII and find its…..matrix. (4mks)
- On the same axis draw the three triangles PQR, PIQIRI and PIIQIIRII and state the co-ordinated of triangle PIQIRI and PIIQIIRII . (6mks)
MARKING SCHEME
-
+1) +3(5x-1) =68x+4+15x-3=623x + 1=623x=5X=5/23
-
- 1-4(2x) +6(2x)2- 4(2x)3+(2x)4
1-8x+24x2-32x3+16x4 - 1-2x =0.96
0.04=2x
0.02=x
1-8(0.02) +24(0.02)2-32(0.02)3+16(0.02)4
1-0.16+0.00096-0.000256+0.00000256
=0.849858556
=0.8499
- 1-4(2x) +6(2x)2- 4(2x)3+(2x)4
- True value √(1+n)= √1.44 = 1.2
Approx. value =1+n/2=1+ 0.044/2 =1.22
=1.22-1.2
=0.02
= 0.02/1.2 ×100=1.67% -
3log8(x+6)-3log8(x-3) =2
log8(x+6)3-log8(x-3)3=log864
log8[((x+6)3)/(x-3)3]=log864
log8[(x+6)/(x-3)]3=log864
3log8((X+6)/(X-3))=log864
log8((x-6)/(x-3))=1/3log864
log 8((x-6)/(x-3))log8641/3
log8 [(x+6)/(x-3) ]= log84
(X+6)/(X-3)=4x+6=4x-12
18=3x
x=6 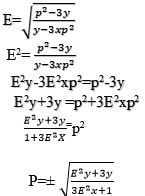
-
. x ≥ 30
2x+3y ≤ 75
Y ≥ 10 - AT × BT = (PT)2
12BT=92
BT= ( 81)/( 12)
BT = 6.5
AB=12-6.75
AB=5.25
Radius =2.6cm - x2+y2-2x+4y=-1
X2+2x+((-2)/2 )2+y2+4y+(4/2 )2=-1+((-2)/2)2+(4/2)2
(x-1)2+(y+2)2=-1+1+4
(x-1)2+(y+2)2=4
Centre (1,-2) radius 2 -
(√3)/(1-√3/2) × (1+ (√3)/2)/(1+ (√3)/2)
(√3+3/2)/(1-3/4) = (√3+3/2)/(1/4)
=4(√3+3/2 )
=4√3+6 -
- . Graph attached
-
g= (52-30)/(60-35)= 22/25
(y-30)/(x-35)=22/25
Y=22/25x -20/( 25)
- Kathwana d=8000, a=40000
40000 +(5×8000) =80000
Siakago r=1.2
40000(1.2)5=40000×2.488
=99533
Difference =99533-80000
=9533 - 6(1-cos2x)-cosx-5=0
6-6 cos2x- cosx-5=0
6a2+a-1=0
6a2+3a-2a-1=0
3a(2a+1)-1(2a+1)=0
3a=1 2a= -1
a=( 1)/3 a=-1/2
a=1/3 and - 1/2
=120° and 240°
70.53° 289° -
-
A
R
90
75
2
3
180
225
- 180+225
5
SH. 81 Per Kg
115/100 × 81
= sh.93.00
-
- dy/dx =2x-1
Y= ∫(2x-1)dx
Y=x2-x+c
5=12-1+C
C=5
Y=x2-x+5 -

- A=πr2
=22/7× 32
=28.2857
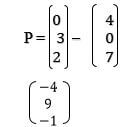
-
-
a (x-5)/(x-2) = (x-2)/(x+2)
(x-5) (x-2)2= (x-2)2X2-3x-10=x2+4x+4
-3x+4x=14X=14
-
- 14 - 5 = 9 = 3
14 - 2 12 4 - t3 = ar2
16=a (3/4 )2
A= 16×16
9
256 =284/9
9 -
a= 259/9r=3/4sum = (a(1-rn))/(1-rn)=(259/9(1-(3/4 )6)/(1-3/4)259/9(1-(3/4 )6 4259/9(1-729/4069)4=93.53
- 14 - 5 = 9 = 3
-
-
-
-
(25/40×2/5×2/3) or (25/40×3/5×1/3)
1/6+1/8
=7/24 -
(15/40×3/5 ×3/4)+ (15/40×2/5 ×1/4)
(25/40×2/5×2/3)+( 25/40×3/5×1/3)
27/160+3/80+1/6+1/8 = 239/480 -
( 15/40×3/5 ×1/4) +( 15/40×2/5 ×3/4)
9/(160 )+9/80
=27/160 -
(15/40×3/5 ×1/4) +( 25/40×2/5×1/3)
9/160+1/12
=67/480
-
-
-
-
OP =1/2(√(32+42)
= 2.5
PV = √(62+ 2.52)=6.964
-
tanθ=6/2
=3
θ= tan -1(3)
71.56°
-
-
-
Slant height vm
VM =√(62+22)
=6.325
VN =√(62+ 1.522)
=6.185 -
(3×4)+(1/2×2×6.325×3)+ 2×1/2×60185×4)
12+18.98+24.74
=55.72
-
-
-
-
71×60×cos60
2130nm -
71×4min =284min
=4hrs 44min
1340hrs = 4hrs 44min
=8:16 am -
71/360×2×6370 cos 60×22/7
=3948.39km -
θ/360×2×22/7×6370=1001
θ=(1001×7×360)/(2×22×6370)
=90°
30°s,42°w
-
-
-
-
median =69.5±0.5
-
Q3 = 77.5± 0.5
Q1 = 58.5 ± 0.5
Quartile deriation = (77.5-58.5)/2
19/2=9.5 -
percentage fail =40%
No of student who
Failed = 40/100×50
=20
Pass mark = 65.5± 0.5
-
-
-
- a=2-t
v=2t-t2 + c
v = 1, t =0
v= 2t- t2+1 - v= 2t-t2+1 32
2(3)-32+1 - 2(2)-22+1
6-9+1- 4-4+1
-2-1
-3m/s
- a=2-t
-
- S=t2-t3/3+t+c ,s=0 t=0
S=t2-t3/3+t - S=t2-t3/3+t t=3
S = (32)- 33/3+3
9-9+3
=3m
- S=t2-t3/3+t+c ,s=0 t=0
-
. t^2-2t-1=0
t=2±√((-2)2-(4×1×-1)
2
=2± 2.828
2
=2.414
-
-
-
1/2×1(46+46+(25+10+1+ 2+10+25)x
-4
-3
-2
-1
0
1
2
3
y
46
25
10
1
-2
1
10
25
= 1/2(92+148)
=120 of units -
.∫-44 (3x2 -2)= x2-2x=56-(-56)=112 of units
- (116-112)/112×100
-
-
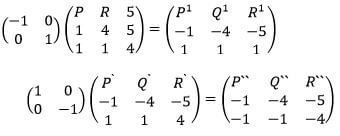
P` (-1,1), Q` (-4,1) and R` (-5,4)
P`` (-1, -1), Q`` (-4, -1) and R`` (-5, -4)-
it’s a reflection in the line y=-x or y+x=0
it’s a rotation through +180°or-180°
about the origin (0,0)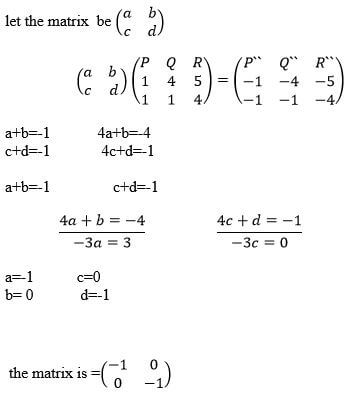
Download Mathematics Paper 2 Questions and Answers - Mincks Group of Schools Mock Examinations 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
