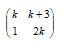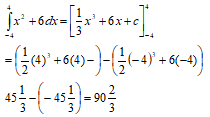Mathematics Paper 2 Questions and Answers - Cekenas Mock Exams 2022

Share via Whatsapp

« Previous Topic
Mathematics Paper 1 Questions and Answers - Cekenas Mock Exams 2022

Next Topic »
English Paper 1 Questions and Answers - Cekenas Mock Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

QUESTIONS

SECTION I: (50MKS)
ATTEMPT ALL THE QUESTIONS FROM THIS SECTION

Find the percentage error in the area of a circle whose radius is 3.5cm measured to 1decimal place. (3mks)
Make h the subject of the formula. (3mks)
q = 1 + rh
l - ht
Simplify and express your answer in the form . State the values of a and b. (Express a and b in the simplest form) (3mks)
2 - 2
2√3 +√2) 2√3 - √2
Given that a²x² + 6ax + k is a perfect square find K. (3mks)
Vector q has a magnitude of 7 and is parallel to vector P. Given that P = 3i - j + 1½k , Express vector q in terms of I, j and k. (3mks)
Given that three number x, y and z are in the ratio 6:4:5. Find the value of
3x - y (3mks)
4y - z
Determine the equation of the normal to the curve y=x² -3x+1 at a point (-2, 3) giving your answer in the form ax+by=c. (3mks)
1. Expand and simplify (1-3x)⁵ upto the term in x³. (1 mks)
2. Hence use your expansion to estimate (0.97)5 correct to 4 decimal places. (2mks)
Two lines x+2y=1 and 2x+3y=3 intersect at T. Find the equation of circle centre T and radius 5 units giving your answer in form of x² + y² +ax+by+c=0 (4 mks)
A quantity P varies jointly as the square of Q and inversely as S. P=3 when Q=5 and S=2. Find the value of P when Q=2 and S=3. (3mks)
Solve for x if sin ^3x/₂ for the range 0≤x≤360º (3mks)
A rectangle ABCD is such that AB=6 and BC=5cm. A variable point P moves inside the rectangle such that AP PB and AP>2.5cm. Show the region where P lies. (3mks)
Chords AB and CD intersects externally at Q. If AB=5cm, BQ=6cm and DQ =4cm. Find the length CQ. (3mks)
$1$
Find the value of k for which the matrix below is singular . (3mks)
$2$
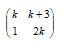
Solve for x in the equation log_n(x + 5) - log_n(x - 3) = ²/₃ (3mks)
The graph below is part of the straight line graph obtained from the initial equation V= apⁿ.
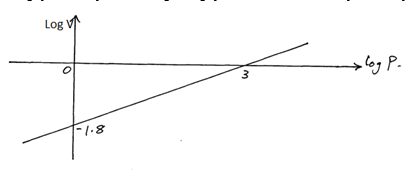
1. Write down the equation of the straight line in form y=mx+c. (1mk)
2. Use the graph to calculate the values of a and n. (3 mks)

SECTION II
ANSWER ONLY FIVE QUESTIONS FROM THIS SECTION

The table below shows income tax rates.

Monthly taxable pay in K£ Rate of tax Ksh in 1 K£

1-435
436-870
871-1305
1306-1740
over 1740 2
3
4
5
6

A company employee earn a monthly basic salary of Ksh 30,000 and is also given allowances amounting to Ksh 10 480.
1. Calculate the total income tax. (5mks)
2. The employee is entitled to a personal tax relief of Ksh 800 per month. Determine the net tax. (1mk)
3. If the employee received a 50% increase in his total income, calculate the corresponding percentage increase on the income tax. (4 mks)
John and James were employed together in a certain year. Their annual salaries in shillings progressed as follows.

1st year 2nd year 3rd year

JOHN 480,000 528,000 576000

JAMES 480,000 528,000 580800
1. Calculate John’s annual salary increment and hence write down an expression for his annual salary in his nth year of employment. (2mks)
2. Calculate James’ annual percentage rate of salary increment and hence write down an expression for his annual salary in his nth year of employment. (3 mks)
3. Calculate their total earnings after 10 years of employment to the nearest Kshs. (5mks)
The number x is chosen at random from the set (0,3,6,9) and the number y is chosen at random from set (0,2,4,6,8). Calculate the probability of each of the following separate events.
1. x > 6 (1mk)
2. x+y=11 (2mks)
3. x > y (2mks)
4. xy=0 (2mks)
5. 10x+y<34 (2mks)
On the surface of the earth A(50ºN, 80ºE) and B(50ºN, 120º E) are two separate places that seem to enjoy trade connected by airlines, taking the radius of the earth as 6370km.
1. If the local time at B is 12.15pm. Find the time at A. (2mks)
2. Calculate the shortest distance between A and B along
  1. Parallel of latitude in nm. (3mks)
  2. A great circle in nm. (3mks)
3. There is a third place C(0,80ºE) that is also enjoying some relationship with town A. Calculate the distance between A and C in km. (2mks)
The diagram shows a sketch of the graph of y=x²+6 and y=22, intersecting at point P and Q.
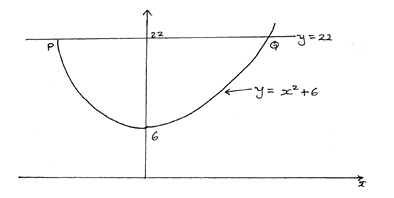
1. Find the co-ordinates of P and Q. (2mks)
2. Estimate the area bounded by line PQ and the curve using the trapezium rule with 8 intervals. (3mks)
3. Calculate the actual area of the enclosed region. (3mks)
4. Calculate the percentage error introduced. (Give your answer to 4 d.p) (2mks)
Mr Mark Opito wishes to take students from wonderful mixed secondary school for a tour. The total number of pupils to be taken should not exceed 60. Each girl must contribute sh 10,000 and each boy shs 15000 and money to be contributed must not exceed sh 120,000. If the trip is to be successful the number of boys must conditionally be greater than girls.
1. Write down inequalities to represent this information taking the number of boys and girls to be x and y respectively. (3mks)
2. Represent the above information on the graph paper provided (4 mks)
3. What is the optimum number of boys and girls to be taken in order to minimize cost and hence determine the cost. (3mks)

Complete the table below. (2mks)

x	0	15	30	45	60	75	90	105	120	135	150	165	180
sin x	0.00	0.26		0.71			1.00	0.97			0.71		0.00
2cos π	2.00	1.93		1.41			0.00	-0.52			-1.41		-2.00
y=sinx+2cosπ	2.00	2.19		2.23			1.00	0.45			-0.70		-2.00

Draw the graph of y=sin x+2 cos x for on the grid provided. (3mks)
Use the graph to solve
1. sin x+2cosπ=0 (1mk)
2. 2(sinx +2cos π) =3 (2mks)
3. tan x+2 = ¹/_{cos x} (2mks)

The following Distribution shows the marks obtained by 72 students in a mathematical test.

Marks 20-29 30-39 40-49 50-59 60-69 70-79 80-89

Frequency 3 13 13 13 14 12 4
1. Use the information above to draw a cumulative frequency (Ogive) curve on the grid provided.
2. Use your graph to estimate
  1. Median (1mk)
  2. Lower quartile and upper quartile (3mks)
  3. Quartile deviation. (1mk)
3. The percentage of candidates passing if the pass mark is 42 marks. (3mks)

MARKING SCHEME

Area = 3.5²π = 12.25π
Maximum = 3.55²π
Minimum = 3.452²π
Error = 3.55²π - 3.45²π = 0.35² 2
P.E = 0.35 x 100
12.25
= 2.85714285
= 2.857%
q = 1 + rh
l - ht
ql - qht = 1 + rh
ql - 1 = rh + qht
= h(r + qt)
h = ql - 1
r + qt
2(2√3 - √2) -2(2√3 + √2)
12 - 2
= 4√3 - 2√2 - 4√3 - 2√2
10
= -4√2
10
= -2√3
5
(^b/₂)² = a.c
^b2/₄ = a.c
(6a)² = a².c
4
36a² = a².c
4
c = 9
IPI = √3² +(-1)² + (³/₂)² = 3.5
hence q = 2p
q = 2(3i - j +1½k)
q = 6i - 2j + 3k
x:y = 6:4
^x/_y = ⁶/₄, x = ⁶/₄y
^y/_z = ⁴/₅ , ^5y/₄ = Z
3(⁶/₄)y-y = ¹⁴/₂₁ ^y/_y = ²/₃
4y + ⁵/_4y
y = x² – 3x+1
^dy/_dx = 2x - 3 At = x = -2
^dy/_dx = -7
⊥a = ¹/₇
y - 3 = ¹/₇
x + 2
-x + 7y = 23
(1-3x)⁵
1. =1+5(-3x)¹ + 10(-3x)² +10(-3x)³
  =1-15x + 90x²- 270x³
2. (0.97)⁵ = (1-3x)⁵x= 0.01
  1 -15(0.01) +90 (0.01)² – 270(0.01)³
  1-0.15 +0.009 +0.00027 = 0.8587
x+2y=-1
2x+3y=3
y=-5 x=-9
centre (-9, -5)
(x+9)² + (y+5)² = 52
x² + y² +18x+10y+81=0
Pa ^Q2/₅
P = ^kQ2/₅
3 =^k(25)/₂
k = ⁶/₂₅
P= ^6Q2/_25.5
P = 6(2) ² =⁸/₂₅
25 x 3
³/₂x = sin-10.85
³/₂x = 58.21, 121.79º , 418.21, 481.79º
x = 33.81º, 81.89º, 278.81º and 321.19º
$5$
11(6) = (x+4)4
66 = 4x+16
x=12.5
CQ=12.5+4
=16.5
k(2k)-1(k+3)=0
2k² – k -3 = 0
(k+1)(2k-3)=0
k=-1
k= ³/₂ = 1½
x + 5 = 82/3
x - 3
x + 5 = 4
x - 3
x + 5 = 4x - 12
x = 5²/₃
1. logV = nLogP + log a
2. n = 0- - 1.8 = ^1.8/₃ = 0.6
  3 - 0
  log a = -1.8
  = 1.8
  = 10^-1 x 0.158
  = 0.0158
1. Taxable income = 40480
  £ 2024
  1-435 =435×2=870
  436-870 435×3 = 1305
  871 -1305 435 ×4 = 1740
  1306-1740 435 × 5 = 2175
  1741 – 2024 284× 6 = 1704
  Payable tax 7794
2. 7794-800 = 6994/=
3. ¹⁵⁰/₁₀₀ x 2024 = 3036
  Extra3036 - 2024 = 1012
  Tax1012 x 6 = 6072
  P.Increase = 6079 x 100
  7794
  = 77.91%
1. 576000-528,000=48000
  a+(n-1)48000
  480,000 +(n-1) 48000
  432,000+48000n
2. 580800 = 528000 = 1.1
  528000 480000
  % rate of increment = 1.1-1 = 10%
  nth term = ar^n-1
  480,000 (1.1)^n-1
3. James = 480000 1.110 - 1
  1.1 - 1
  = 7649964
  John = 10/2 (2 x 480000 + 9 x 4800)
  = 4802160
  Total = 7649964 + 4802160
  = 12452124
1. ¼
2. 0 3 6 9
  
  0 0 3 6 9
  
  2 2 5 8 11
  
  4 4 7 10 13
  
  6 6 9 12 15
  
  8 8 11 14 17
  
  ²/₂₀ = ¹/₁₀
3. 0 3 6 9
  
  0 00 03 06 09
  
  2 20 23 26 29
  
  4 40 43 46 49
  
  6 60 63 66 69
  
  8 86 83 86 89
  
  ¹⁰/₂₀ = ½
4. 0 3 6 9
  
  0 0 0 0 0
  
  2 0 6 12 18
  
  4 0 12 24 36
  
  6 0 18 36 54
  
  8 0 24 48 72
  
  ⁸/₂₀ = ²/₅
5. 0 3 6 9
  
  0 0 30 60 90
  
  2 2 32 62 92
  
  4 4 34 64 94
  
  6 6 36 66 96
  
  8 8 38 68 98
  
  ⁷/₂₀
1. longitude difference =120-80 = 40º
  Time difference = 40×4 = 1600 =2hrs 40 min
  Time in A = 12.15 - 2.40 = 9.35am
2. 1. AB=60× 40 cos 50º
    =2400× 0.6424
    =1542.69nm
  2. r=6370 cos 50
    =4094.50
    AB=2 rcos 70
    = 2× 4094 .56cos 70
    =2800.8
    AB=2Rcos ^ℑ/₂
    sin^θ/₂ = ^AB/_BRsin^θ/₂ = 2850.8
    2 x 6370
    sin^θ/₂ = 0.21984
    ^θ/₂ = 12.70
    θ = 25.4
    AB = 25.4 x 60
    1524mm
3. AC = ⁵⁰/₃₆₀2πR
  ⁵⁰/₃₆₀x 2 x ²²/₇ x 6370
  = 5558.9km
1. 22 = x² + 6
  x² = 16
  x = ± 4
  P =(-4,22) Q =(4,22)
2. x -4 -3 -2 -1 0 1 2 3 4
  
  y 22 15 10 7 6 7 10 15 22
  
  b1 0 7 12 15 16 15 12 7 0
  
  A = 1(½(0+0)+7+12+15+16+15+7)
  = 1(84)
  = 84sq units
  8 x 22 = 176
3. $6$
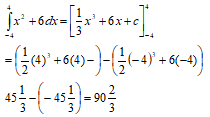
  Actual 176 - 90²/₃ = 85¹/₃
4. P.E = 1¹/₃ x 100
  85¹/₃
1. 1. Let the number of girls be x boys y
    3x+2y 24
    x+y 60
  2. y > x
    x ≥ 0
    y ≥ 0
    $7$
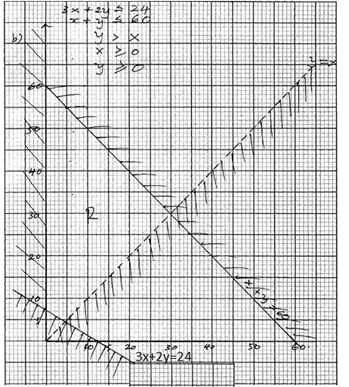
2. Minimum cost appears at (0,12)
  Cost 15000(0) + 10000(12)
  =120000

x	0	15	30	45	60	75	90	105	120	135	150	165	180
sin x	0.00	0.26	0.50	0.71	0.87	0.97	1.00	0.97	0.87	0.71	0.50	0.26	0.00
2cos π	2.00	1.93	1.73	1.41	1.00	0.52	0.00	0.00	-1.00	-1.41	-1.73	-1.93	-2.00
y=sinx+2cosπ	2.00	2.19	2.23	2.21	1.87	1.49	1.49	1.00	-0.13	-0.70	-1.23	-1.67	-2.00

$8$

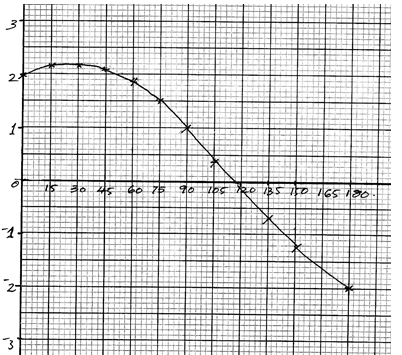
1. x=117º
2. x=75º ± 3º sinx=2cos x=1
3. Tan x + 2 = ¹/_{cos x}
  sinx+2cosx=1
  x=90º

1. Marks 20-29 30-39 40-49 50-59 60-69 70-79 80-89
  
  Frequency 3 13 13 13 14 12 4
  
  cf 3 16 29 43 56 68 72
  
  $9$
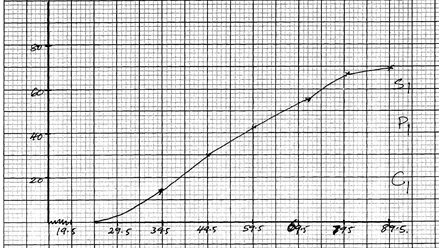
2. Median =54.5
  Q1 = 41.5
  Q2 = 68.5
  68.5 - 41.5 = 13.5
  2
  72-18 x 100
  72
  = ⁵⁴/₇₂ x 100
  = 75%