Mathematics Paper 2 Questions and Answers - Alliance Mock Examinations 2022

QUESTIONS

SECTION 1-50 MARKS (ANSWER ALL THE QUESTIONS)

1. A stop watch reads correct to ¹/₅ seconds. Two races are timed as 49³/₅ seconds and 49⁴/₅ seconds. Calculate the maximum percentage error in sum of these two timings (3 marks)
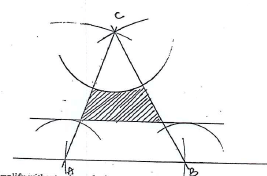
2. Construct, using a scale of 1:100 construct a trianguiar plot ABC where AB=6m, AC-7m and BC-7.5m using AB as the base. Cows are allowed to graze inside the plot provided that they are at least 2 meters from AB and more than 3 meters from C. Indicate by shading the area available for grazing. (4 marks)
3. Simplify without using calculators or mathematical tables, the value of(3 marks)
   8 - ^√60/₂ + √5+√3
                    √5-√3
4. Use binomial expansion to determine the value of (1½)⁵ (3 marks)
5. The mean and standard deviation of the marks scored by a group of 10 students was found to be 47 and 11 respectively. An eleventh student had a score of 58 marks. Calculate the mean and standard deviation of the 11 students. (4 marks)
6. Two pipes fill a swimming bath in 12 hours. The larger pipe is 33¹/₃ more efficient than the smaller pipe. How long does the larger pipe take to fill the bath? (3 marks)
7. Given that S = (1 - rⁿ) make n the subject of the formula.
                             1 - r
8. State the amplitude and the period of the following function y=tan 3x
9. In a Geometric Progression, the first term is 2 and the common ratio is 2. Given that the product of the last two terms of the GP is 8192, find the sum of the last two terms. (3 marks)
10. Given that x=m+ n, and m varies directly as y while n varies directly as the square of y. If x=16, y=2 and when x=33, y=3. Find x when y=8. (3 marks)
11. A curve is such that ^dy/_dx = 4-x and the point (2,9) lies on the curve. Find the equation of the curve. (3 marks)
12. Given that p=2i-3j+k and q-3i-4j-3k, a point R divides a line PQ externally in the ratio of 4:1. Find the coordinates of R. (3 marks)
13. Given that x and y are both positive, solve the equations log(xy) = 7 and log(^x/_y)=1 (3marks)
14. Use the mid-ordinate rule to estimate the area enclosed by the curve y = x²-9, x-axis and the lines x=2 and x-5 using six strips (3marks)
15. Find the value of p if ∫³₀(px² + 2x + 3)dx = 54
16. Solve for x in the domain 0≤x≤2π^c
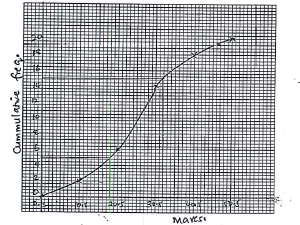
    2cos2x= -0.7071
17. The table below shows the frequency distribution of marks scored by students in a test.
    

    Marks	1-10	11-20	21-30	31-40	41-50
    Frequency	2	4	8	4	2

    1. On the grid provided, draw an ogive for the data.
    2. Use your graph to determine;
       1. The pass mark if only 6 students passed the exam.
       2. The quartile deviation
    3. Range of marks scored by the middle 60 % of the students
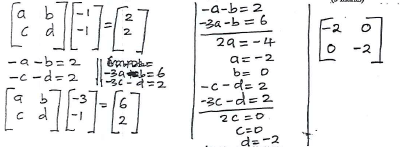
18. A triangle ABC with vertices at A (1,-1), B (3,-1) and C (1, 3) is mapped onto triangle A'B'C' by a transformation whose matrix is(^-1₀ ⁰₁) Triangle A'B'C' is then mapped onto A''B''C'' with vertices at A"(2, 2), B"(6,2) and C''(2,-6) by a second transformation.
    1. Find the coordinates of A'B'C' (3 marks)
    2. Find the matrix which maps A'B'C' onto A''B''C''. (3 marks)
    3. Determine the ratio of the area of triangle A'B'C' to triangle A"B''C"(1 mark)
    4. Find the transformation matrix which maps A''B''C'' onto ABC (3 marks)
19. The table below shows the taxation rates for income earned.
    

    Income in ksh pm	Tax rates (%)
    1-9680	10
    9681 - 18800	12
    18801 - 27920	20
    27921 - 37040	25
    Excess over 37041	30

    In that year, Mr. Hamisi paid a net tax of KSh. 5,512 per month. He is entitled to the following monthly allowances:
    House Allowance -Shs. 10,000
    Medical Allowance -Shs. 2400
    Acting Allowance -Shs. 2820.
    He is entitled to a monthly personal relief of KShs. 1162 while 7.5% of his basic salary is tax-exempted.
    1. Calculate Mr. Hamisi's monthly basic salary in KSh. (7 Marks)
    2. The following deductions also made every month.
       1. N.H.I.F. KSh. 320
       2. Co-operative society shares KSh. 6000
       3. Union dues KSh. 200
          Calculate his net monthly salary. (3 Marks)
20. The acceleration of a particle, t seconds after passing a fixed-point P is given by a 4t-7. Given that the initial velocity of the particle is 5m/s, find;
    1. Its acceleration when t = 4 seconds
    2. Its velocity when t=3 seconds
    3. Values of t when the particle is momentarily at rest
    4. Its maximum velocity
21. Mr. Mairura has two lorries A and B used to transport at least 42 tons of potatoes to the market. Lorry A carries 4 tons of potatoes per trip while lorry B carries 6 tons of potatoes per trip. Lorry A uses 2 liters of fuel per trip while lorry uses 4 liters of fuel per trip. The two lorries are to less than 24 liters of fuel. The number of trips made by lorry A should be less than the number of trips made by lorry B. Lorry A should make more than 4 trips.
    1. Taking X to represent the number of trips made by lorry A and Y to represent the number of trips made by lorry B, write the inequalities that represent the above information (4marks)
    2. Plot the inequalities above in the graph provided below (4 marks)
    3. If Lorry A makes sh. 35,000 per trip and Lorry B makes sh.28,000 per trip, use the graph above to determine the number of trips made by lorry A and by lorry B to deliver the greatest number of potatoes and hence find the maximum profit. (2marks)
22. The position of 3 cities P, Q and R are (15°N, 20°W) (50°N, 20°W) and (50°N, 60°E) respectively.
    1. Find the distance in nautical miles between:
       1. Cities P and Q (2 marks)
       2. Cities Q and R along a circle of latitudes
    2. A plane left city P at 0250h and flew to city Q where it stopped for 3 hours then flew on to city R, maintaining a ground speed of 900 knots throughout. Calculate:
       1. The local time at city R when the plane left city P
       2. The local time (to the nearest minute) at city R when the plane landed at R. (3 marks)
23. The figure below represents a cuboid ABCDEFGH, with AB = 7 cm, BC = 24 cm andCF = 7.2 cm. M and N are the mid-points of EF and DC respectively.
    
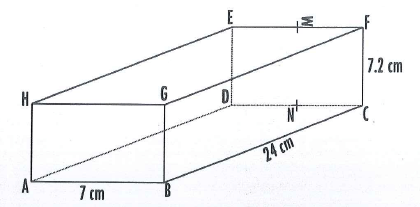
    Calculate to 2 decimal places the:
    1. Angle AF makes with the plane ABCD (3 marks)
    2. Angle between the lines HF and AB. (2 marks)
    3. Angle between the planes GHEF and ABFE (2 marks)
    4. Angle between BM and the plane ABCD (3 marks)
24.      
    1. A jewel is guarded by three guards A, B and C in that order. On his way in, the probability of a thief getting caught by guard A is ²/₃, by B is ³/₇ and by C is ¼. On his way out, the probability of being caught by guard C is ⁴/₅ , by B is ¹/₃ and by guard A is ²/₅. Calculate the probability that:
       1. The jewel is stolen and the thief escapes. (2 marks)
       2. The thief was caught by guard C
    2. Albert, Bonny and Charles competed in a game of chess. Their probabilities of winning the game are ²/₅, ³/₅ and ¹/₁₀ respectively.
       1. Draw a probability tree diagram to show all the possible outcomes. (2 marks)
       2. Calculate the probability that;
          1. No one loses the game. (2 marks)
          2. Only one of them wins the game.

MARKING SCHEME

1. AE =½ x ¹/5 = ¹/10
   AE in sum = ¹/10 x 2 = 1/5
   % error =¹/5 x 100
   ⁴⁹³/5 + ⁴⁹⁴/5
   = 0.2012%
2.    
   
3. ^√60/2 = √15x√4
                   2
   = 2√15
         2
   = √15
   √5 + 3 (√5 + 3) = 8 +2√5
   √5 - 3  √5 +√3          2
   = 4 +√15
   8 - √15 + 4 + √15
   = 12
4. (1)⁵ + 5(1⁴)(½) + 10(13)(½)² + 10(12)(½)³ + 5(1)(½)⁴ + (½)⁵
   = 1 + ⁵/2 + ⁵/2 + ⁵/4 + ⁵/16 + ¹/32
   = 7.59375
5. Σfx = 47 x 10 = 470
   new(x) = 470 + 58
                     11
   = 48
   sd = √Σfx² - (x)²
              Σf
   11² = Σfx² - 47²
             10
   Σfx² = 23300
   new sd =√23300 - 48²
                      11
   = 10.95
6. bigger        smaller
   133¹/3%x      x
   1hr = ¹/x + ⁴/3x = ¹/12
   ⁷/3x = ¹/12
   ¾  x = 28
   larger pipe = ¾ x 28
   = 21hrs
7. S - Sr = 1 - rⁿ
   8n = 1 - s + sr
   nlog r = log(1 - S + Sr)
   n = log(1 - S + Sr)
               log r
8. a = undefined
   period = 180
9. (ar^n-1)(ar^n-2) = 8192
   2 x 2^n-1 x 2 x 2^n-2 = 213
   2^n-1 = 2¹³
   n = 7
   last = 2 x 2⁶ = 128
   2nd = 2 x 2⁵ = 64
   sum = 128 + 64
   = 192
10. m x y = m=ky
    n x y² = n=ay²
    x = ky + ay²
    16 = 2k + 4a
    33 = 3k + 9a
    k = 2
    a = 3
    x = 2y + 3y²
    x = 2(8) + 3(64)
    x = 208
11. y = ∫(4 - x)dx
    y = 4x - x² + c
                 2
    9 = 8-2 + c
    c = 3
    y = 4x - x² + 3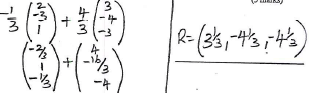
12. 
    
    m:n
    4:1
13. log x + log y = 7
    log x - log y = 1
    2log y = 6
    log y = 3
    y = 1000
    x = 10000
14. A = 0.5(3.9375 + 1.4375 + 1.5625 + 5.0625 + 9.0625 + 13.5625)
    A = 17.3125 sq umits
15. [Px³ + x² + 3x]³₀ = 54
    9p + 18 = 54
    9p = 36
    p = 4
16. cos 2x = 0.35355
    2x = 110.71, 249.29, 470.71, 609.29
    x = 55.355, 124.645, 235.355, 304.645
    x = 0.3075c, 0.6923c, 1.307c, 1.6925c
17. 
    

    Marks	1-10	11-20	21-30	31-40	41-50
    Frequency	2	4	8	4	2
    cf	2	6	14	18	20

    1.  
        
    2.         
       1. 30.5 marks
       2. 0.25 x 20 = 5th
          = 18.5
          0.75 x 20 = 15th
          = 32.5
          32.5 - 18.5
                  2 
          = 7
    3. 0.2 x 20 = 4th → 16.5
       0.8 x 20 = 16th → 34.5
       range → 16.5 to 34.5
18.    
    1.    
       
    2.  
       
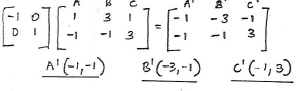
    3. ASF = 4
    4.  
       
19.      
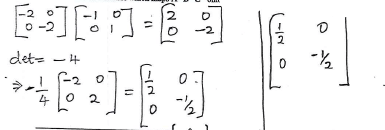
    1. gross tax = 5512 + 1162
       = 6674
       9680 x 0.1 = 968
       9120 x 0.15 = 1368
       9120 x 0.2 = 1824
       9120 x 0.25 = 2280
       0.3 x y = 234
       y = 780
       TI = 9680 + 3(9120) + 780
       = 37820
       BS = 37820 - (10000 + 2400 + 2820)
       = 22600
       22600 x 100
       92.5
       = 24.432.43
    2. deducstions = 320 + 6000 + 200 + 5512 = 12032
       net salary = 39652.43 - 12032
       = 27620.43
20.      
    1. a = 4(4) - 7
       = 9ms^-2
    2. v = ∫(4t - 7)dt
       v = 2t² - 7t + c
       s = c
       v = 2t² - 7t + 5
       v = 2(9) - 4(3) + 5
       v = 2m/s
    3. v = 0
       2t² - 7t + 5 = 0
       t² - 3.5t = -2.5
       t² - 3.5t + (-1.75)² = 0.5625
       t - 1.75 ± 0.75
       t = 1.75 ± 0.75
       t = 1sec or t = 2.5sec
    4. a = 0
       0 = 4t - 7
       t = 1.75 sec
       v = 2(3.0625) - 7(1.75) + 5
       v = -1.125m/s
21.    
    1.       
       1. 4x + 6y ≤ 42
       2. 2x + 4y ≤ 24
       3. x < y
       4. x > 4
       5. x ≥ 0
    2.   
       
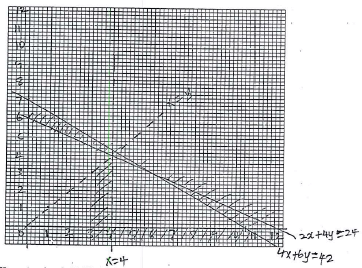
    3. (6,3) → (6 x 35000) + (3 x 28000)
       = 294000
22.      
    1.    
       1. 
          
          D  = 60 x 35
          = 2100nm
       2. D = 60 x 80 cos 50
          D = 3085.38nm
    2.    
       1. 80 x 4 = 320min
          = 5hrs 20min
          0250 + 520 = 8:10
          = 0810hrs
       2. Time from P to Q
          = 2100 = 2¹/3
               900
          Q to R = 3085.38 = 3hrs26min
                           900
          total time = 3hrs26min + 2hr20min + 3hrs
          = 8hrs46mins
          = 16:56hrs
23.  
       
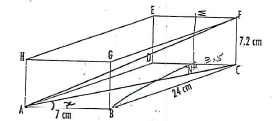
    1. AC = √24² + 7²
       = 25cm
       tan = ^7.2/25
       = 16.07
    2. tan x = ²⁴/7
       x = 73.74º
    3. tanθ = ^7.2/24
       = 16.70º
    4. tanθ = ^7.2/23.74
       BN = √24² - 3.5²
       θ =  16.87º
24.        
    1.      
       1.  
          
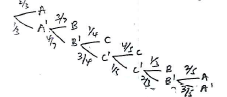
          ¹/₃ x ⁴/₇ x ¾ x ¹/₅ x ²/₃ x ³/₅
          = ²/₁₇₅
       2. (¹/₃ x ⁴/₇ x ¼) + (/₃ x ⁴/₇ x ¾ x 4/5) 
          = ⁴/₈₄ + ⁴/₃₅
          = ¹⁷/₁₀₅
    2.    
       1.      
          
       2.    
          1. P(ABC)
             = ²/₅ x ³/₅ x ¹/₁₀ = ³/₁₂₅
          2. ( ²/₅ x  ²/₅ x ⁹/₁₀) + (³/₅ x ³/₅ x ⁹/₁₀) + (³/₅ x ²/₅ x ¹/₁₀)
             = ¹²³/₂₅₀