Mathematics Paper 2 Questions and Answers - Bondo Joint Mocks Exams 2022

Questions

Instructions to candidates

•  This paper consists of TWO sections: Section I and only five questions form Section II
• Answer ALL the questions in Section I and only five questions from Section II
• All answers and workings must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I (50MARKS)
Answer all questions in the spaces provided

1. Tap A can fill a tank in 10 minutes, tap B can fill the same tank in 20 minutes. Tap C can empty the tank in 30 minutes. The three taps are left open for 5 minutes, after which tap A is closed. How long does it take to fill the remaining part of the tank (4 marks)
2. Make m the subject of the formula; (3 marks)
3. Solve for x in the equation; log₂81 + log₂(x2) = 1 (3 marks)
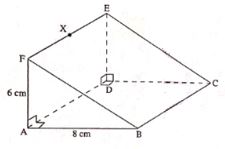
4. The figure below shows a prism in which FA = 6cm and AB = 8cm. X is a point on the edge FE such that < FBX = 45˚. Calculate the angle between BX and the plane ABCD (3 marks)
   
5. Two towns X and Y on latitude 15˚S differ in longitude by 36˚12'. Find the distance in km between them along their parallel of latitude to 4 s.f (Take radius of the earth to be 6370km and ) (3mks)
6. Vector a passes through the points (5, 10) and (3, 5) and vector b passes through (x, 6) and (-5, -4). If a and b are parallel, find the value of x (3mks)
7. The velocity Vms -1 of particle in motion is given by V =3t 2 – t +4, where t is time in seconds. Calculate the distance traveled by the particle between the time t=1 second and t=5 seconds. (4 marks)
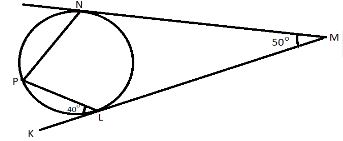
8. In the figure below, line KLM and NM are tangents to the circle at L and N respectively. = 50˚ and < = 40˚. Find the size of < (3 marks)
   
9. A man deposits ksh. 50 000 in an investment account which pays 12% interest per annum compounded semi-annually. Find the amount in the bank after three years to the nearest shillings. (3 marks)
10. Find the percentage error in the area of a sphere whose diameter is 7.0 (3 marks)
11. Solve for x in 2 cos x = sin²x + 2, for 0 ≤ x ≤ 360˚ (4 marks)
12. The fifth term of an arithmetic progression is 11 and the twenty fifth term is 51. Calculate the first term and the common difference of the progression. (3 marks)
13. A variable y varies as the square of x and inversely as the square root of z. Find the percentage change in y when x is increased by 5% and z reduced by 19%. (3 marks)
14. Under a transformation whose matrix is A = , a triangle whose area is 12.5cm 2 is mapped onto a triangle whose area is 50 cm 2 . Find the two possible values of a. (3 marks)
15. The probability of a team losing a game is . The team plays the game until it wins. Determine the probability that the team wins in the fifth round (2 marks)
16.      
    1. Expand and simplify the expansion (10 + ²/_X)⁵ (1 mark)
    2. Use the expansion in (a) above to find the value of 14⁵ (2 marks)

SECTION II ( 50 MARKS)
Answer any FIVE questions from this section in the space provided

17. The table below shows the marks of 90 students in a biology exam. 
    

    Marks	5 - 9	10 -14	15 -19	20 - 24	25 - 29	30 - 34	35 - 39
    NO. of students	2	13	Y	23	14	6	1

    1. Find the value of y (2 marks)
    2. State the frequency of the modal class (1 mark)
    3. Using a working mean of 22, calculate the;
       1. Mean mark (5 marks)
       2. Standard deviation (2 marks)
18.   
    1. Using a ruler and a pair of compasses only , construct triangle ABC in which AB = 9cm. BC = 8.5cm and BAC= 60˚
    2. On the same side of AB as C:
       1. Determine the locus of a point P such that ˚ (3 marks)
       2. Construct the locus of R such that AR 4 cm. (2 marks)
       3. Determine the region T such that angle ACT angle BCT (2 marks)
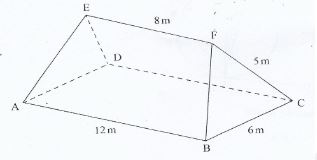
19. The figure ABCDEF below represents a roof of a house
    AB= DC = 12m, BC=AD = 6 m, AE=BF = CF = DE = 5 m and EF= 8m
    
    
    1. Calculate correct to 2 decimal places, the perpendicular distance of EF from the plane ABCD (4 marks)
    2. Calculate the angle between
       1. The planes ADE and ABCD (2 marks)
       2. The line AE and the plane ABCD, correct to 1 decimal place (2 marks)
       3. The planes ABFE and DCFE, correct to 1 decimal place. (2 marks)
20. The position of two towns A and B on the earths surface are (36N , 49˚ E) and (36˚ N , 131˚ W ) respectively( Earth’s radius = 6370 km and = ) :
    1. Find the longitudinal difference between the two towns (2 marks)
    2. Calculate the distance between the towns :
       1. Along the parallel of latitude (in km) (3 marks)
       2. Along the great circle in km (2 marks)
    3. Another town C, is 840 km due East to town B . Locate the position of town C. (3 marks)
21. Cherera is required to make two types of dresses .Type A and type B . The total number of dresses must not exceed 500.Dresses of type B must not be less than dresses of type A.
    She must make at least 200 dresses of type A. Let x represent the number of dresses of type A and y represent the number of dresses of type B.
    1. Write down the inequalities that describe the given conditions above (3 marks)
    2. On the grid provided, draw the inequalities (3 marks)
    3. Profits were as follows;
       Type A Kshs. 900 per dress
       Type b Kshs. 700 per dress
       Determine the maximum possible profit (4 marks)
22. A quadrilateral with vertices at K(1,1), L(4,1), M(2,3) and N(1,3) is transformed by a matrix. T= to a quadrilateral KʹLʹMʹNʹ.
    1. Determine the coordinates of the image (2 marks)
    2. On the grid provided draw KLMN and K’L’M’N’ (2 marks)
    3. Describe the transformation that maps KLMN onto K’L’M’N’ (1 mark)
    4.      
       1. Find K”L”M”N” the image of K’L’M’N’ under the transformation matrix (2 marks)
          R=
       2. On the same grid draw K”L”M”N” (1mark)
    5. Find a matrix which maps K”L”M”N” onto KLMN. (2 marks)
23. A particle moves in a straight line from appoint P with an acceleration (5-12t) m/s 2 , t seconds after the start. Given that the particle started with a velocity of 3m/s.
    1. Find the velocity in terms of t (3 marks)
    2. Determine the velocity after 2 seconds (2 marks)
    3. Determine the maximum velocity attained by the particle (3 marks)
    4. Calculate the distance covered during the 3 rd second (2 marks)
24. Income tax is charged on annual income at the rate shown below
    

    Taxable income in kshs. Per month	Rate (Kshs./k£ )
    1 - 2300	2
    2301 - 4600	3
    4601 - 6900	5
    6901 - 9200	7
    9201 - 11500	9
    11501 And Above	10

    Mr. Otieno is a civil servant and earns kshs. 12,000 PM. He lives in a company house for which he pays nominal rent of kshs 1000 PM. He is entitled to a personal relief of ksh 1056 PM and insurance relief of kshs. 480 PM.
    1. Calculate;
       1. Mr. Otienos taxable income (3 marks)
       2. Calculate his P.A.Y.E. (5 marks)
       3. Calculate his net monthly salary in shillings if he pays NHIF of Kshs. 320 p.m. And sacco loan repayment of Kshs.3600 p.m. (2 marks)