QUESTIONS
SECTION 1 (50 MARKS)
Answer all the questions in the space provided below each question
- Without using mathematical tables or calculator evaluate
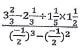 (3marks)
(3marks) - Find the equation of a straight line that passes through the points A (2,-3) and B-5,1). Express your answer in the form ax + by = c where a, b and care integers. (3marks)
- Solve for θ if
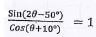 (3marks)
(3marks) - A Swimming pool can be emptied by 3 pipes P, Q and working together in 33/4 hours. Pipe P and working alone takes 71/2 hours and 111/4 respectively. Determine how long pipe R working alone would take to empty the swimming pool. (3marks)
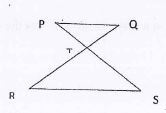
- In the figure below PQ || RS.PS and RQ intersect at T. If PT: PS = 2:5 and QT = 3.5 cm, calculate correct to 2 decimal place RQ. (3 marks)
- A is the point (2, 3, 4) and B is the point (X, 6, 8).Determine the possible values of X if |AB| =13 (4 marks)
- A metal hemisphere of radius 16 cm is melted down and cast into a cone of radius 8cm.Calculate the volume of the cone. (3marks)
- Five of the iterior angles in a nonagon are 160° and the remaining are each x0. Find the possible values of x. (3marks)
- Calculate the quartile deviation of the following set of data (4marks)
Marks 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 No. of students 3 5 8 12 15 11 9 4 - A metallic pipe which is 21 meters long has an internal radius of 13 cm and an external radius of 15 cm. if the density of the metal is 8000 kg/m3, find its mass. (Take π = 22/7). (4 marks)
- Muthoni, Chebet and Amina contributed ksh 50,000, ksh 40,000 and ksh 25,000 respectively to start a business. After some time they realized a profit which was shared in the ratio of their contribution. If Aminas share was ksh 10,000, by how much was Muthoni's share more than that of Chebet's. (3marks)
- The cost of two jackets and 3 shirts was 1800. After the cost of a jacket and that of a shirt were increased by 20%, the cost of 6 jackets and 2 shirts was ksh 4,800. Calculate new total cost of 5 jackets and 4 shirts. (3 marks)
- Without using mathematical tables evaluate
 (3marks)
(3marks) - Using a ruler and a pair of compass only, construct a rhombus AB< CD such that AC = 10 cm and ∠BAD = 60° (3marks)
- Without using a calculator or mathematical tables, evaluate
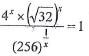 (3marks)
(3marks) - A point P divides a line AB externally in the ratio 4:3. Given that A is (-2, 4) and point B (2,-3). Find the coordinates of T. (3marks)
SECTION II (50MARKS)
Answer only five questions from this section.
- In the figure below, AC=14 cm, AD = 16 cm, DC = 11 cm, and B is a point on AC
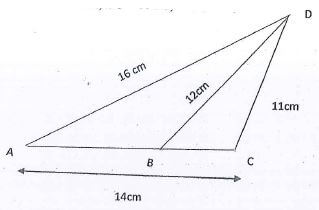
- Calculate, correct to 2d.p
- ∠BAD (3marks)
- The size of obtuse ∠ABD (3marks)
- Calculate correct to 1 decimal place:
- The length of AB (2marks)
- The area of triangle BCD (2marks)
- Calculate, correct to 2d.p
- The following table shows heights of 100 seedlings each measured to the nearest cm.
Height (cm) Frequency 70 - 79 14 80 - 84 16 85 - 89 18 90 - 94 20 95 - 99 17 100 - 109 15 - Calculate the differences between the mean and the median. (6marks)
- Draw a frequency polygon to illustrate the above information (4marks)

- Two towns P and Q are 280 km apart. A bus left town P at 9.30 am and travelled to Q at an average speed of 80 km/h. After 30 minutes, a car left town p for Q and travelled at an average speed of 100 km/h.
- Determine:
- The time when the car caught up with the bus. (3marks)
- The distance of the car from town Q when it overtook the bus. (3marks)
- After the car overtook the bus, it accelerated for 6 minutes to a speed of 120 km/h. It moved with that speed for 30 minutes after which breaks are applied and came to rest at town T after 3 minutes. Determine the distance travelled by the car in 39 minutes. (4marks)
- Determine:
-
- Complete the table of values for the equation y .-2x2 + 3x + 6. (2 marks)
x -3 -2 -1 0 1 2 3 4 y - Use the values above to draw the graph of y = -2x2 + 3x + 6. (3marks)

- Using the graph drawn above Solve the oquations:
- 2x2 = 3x +6 (2 marks)
- -2x2 + x + 9 = 0 (3marks)
- Complete the table of values for the equation y .-2x2 + 3x + 6. (2 marks)
- A trader deals with two types of Millet, type A and type B. type A costs ksh 400 per bag and type B costs ksh 350 per bag.
- The trader mixes 30 bags of type A and 50 bags of type B. If she sells the mixture at a profit of 20%, calculate the selling price of one bag of the mixture. (4 marks)
- The trader now mixes type A and type B in the ratio x: y respectively. If the cost of the mixture is ksh 383.50 per bag, find the ratio x:y. (4marks)
- The trader mixes one bag of the mixture in part (a) with one bag of the mixture in part (b) above. Calculate the ratio of type A millet to type B millet in this mixture. (2marks)
- The equation of a line L1 is 3y + 2x = 10
- Find in form of y=mx+c,where m and care constants:
- The equation of line L2 passing through N (-5,2) and parallel to L1 (2 marks)
- The equation of line L3 perpendicular to L2 at M (1,-8) (3marks)
- Find the angle of inclination of the line L, with the horizontal. (2marks)
- Find the magnitude of MN. (3marks)
- Find in form of y=mx+c,where m and care constants:
- In the figure below A, B, C and D are points on the circle Centre O. ACF and EDFG are straight lines. Line EG is a tangent to the circle at D. ∠CDF = 35° and ∠CFG = 130°
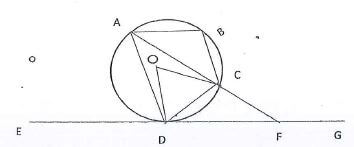
- Calculate the Size of
- ∠OCD (2 marks)
- ∠EDA (1 mark)
- ∠ABC (2 marks)
- Given that CFo 6.7 cm and DF = 8.5 cm, Calculate to 3 significant figures:
- The length of DC. (3marks)
- The radius of the circle. (3marks)
- Calculate the Size of
- The product of the first three terms of a geometric progression is 64.If the first term is a and the common ratio is r,
- Express r in terms of a. (3marks)
- Given that the sum of the three terms is 14
- Find the value of a and r and hence write down two possible sequence up to the 4th term. (5 marks)
- Find the product of the 50th terms of the two sequence. (2marks)
MARKING SCHEME
SECTION 1 (50 MARKS)
Answer all the questions in the space provided below each question
- Without using mathematical tables or calculator evaluate
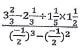 (3marks)
(3marks)
11/3 - 7/3 x 5/6 x 3/2
11/3 - 35/12
44 - 35
12
9/12
3/4
Denominator
-1/8 - 1/4
- 1 - 2
8
-3/8
3/4 x 8/-3
= -2 - Find the equation of a straight line that passes through the points A (2,-3) and B-5,1). Express your answer in the form ax + by = c where a, b and care integers. (3marks)
gradient =
1 - 3 = -1
- 5 - 2 7
y + 3 = -4
x - 2 7
-4 (x - 2) = 7 (y + 3)
-4x + 8 = 7y + 21
-4x - 7y = 13
4x + 7y = -13 - Solve for θ if
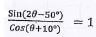 (3marks)
(3marks)
sin(2θ - 50º) = cos (θ + 10º)
sin (2θ - 50º) = sin 90 - (θ + 10º)
20 -50 = 90 - θ - 10
3θ = 130
θ = 431/3 or 43.33º - A Swimming pool can be emptied by 3 pipes P, Q and working together in 33/4 hours. Pipe P and working alone takes 71/2 hours and 111/4 respectively. Determine how long pipe R working alone would take to empty the swimming pool. (3marks)
ans = 221/2 hrs - In the figure below PQ || RS.PS and RQ intersect at T. If PT: PS = 2:5 and QT = 3.5 cm, calculate correct to 2 decimal place RQ. (3 marks)

RT/3.5 = 3/2
RT = 3/2 x 3.5
= 5.25
RQ = 5.25 + 3.5
= 8.75 - A is the point (2, 3, 4) and B is the point (X, 6, 8).Determine the possible values of X if |AB| =13 (4 marks)
(x - 2)2 + (6 - 3)2 + (8 - 4)2 = 169
x2 - 4x + 4 + 9 + 16 = 169
x2 - 4x - 140 = 0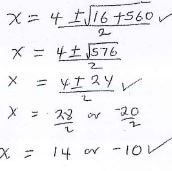
- A metal hemisphere of radius 16 cm is melted down and cast into a cone of radius 8cm.Calculate the volume of the cone. (3marks)
1/2 x 4/3 x 22/7 x 163 = 1/3 x 22/7 x 64 x h
h = 1/2 x 4/3 x 3 x 7 x 22/7 x 163
64 x 22
h = 128
volume of cone = 1/3 x 22/7 x 64 x 128
= 8,582 - Five of the interior angles in a nonagon are 160° and the remaining are each x0. Find the possible values of x. (3marks)
sum of interior angles of nonagon = 180(9 - 2)
= 1260
160 x 5 + 4x = 1260
4x = 1260 - 800
x = 460
4
x = 115 - Calculate the quartile deviation of the following set of data (4marks)
Q1 = 1/4 x 67 = 16.75Marks 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 No. of students 3 5 8 12 15 11 9 4 cf 3 8 16 28 43 54 63 67
50.5 + (16.75 - 16)10
12
50.5 + 0.625
∠ 1.125
Q3 = 3/4 x 67 = 50.25
70.5 + (50.25 - 43) x 10
11
70.5 + 6.591
= 77.09
Quartile deviation =
77.09 - 51.125 = 25.965
2 2
= 12.98 - A metallic pipe which is 21 meters long has an internal radius of 13 cm and an external radius of 15 cm. if the density of the metal is 8000 kg/m3, find its mass. (Take π = 22/7). (4 marks)
external volume = 22/7 x 7.52 x 2100 = 371,250
internal volume = 22/7 x 6.52 x 2100 = 278,850
volume of material = 371,250 - 278,250 = 92,400cm3
= 0.924m3
8000 = mass
0.924
mass = 7,392 kg - Muthoni, Chebet and Amina contributed ksh 50,000, ksh 40,000 and ksh 25,000 respectively to start a business. After some time they realized a profit which was shared in the ratio of their contribution. If Aminas share was ksh 10,000, by how much was Muthoni's share more than that of Chebet's. (3marks)
M:C:A = 50000:40000:25000
=10:8:5
5/23 x 10000
x = 10000 x 23
5
= 46000
muthoni = 10/23 x 46000 = 20000
chebet = 8/23 x 46000 = 8000
20000- 8000
= 12000 - The cost of two jackets and 3 shirts was 1800. After the cost of a jacket and that of a shirt were increased by 20%, the cost of 6 jackets and 2 shirts was ksh 4,800. Calculate new total cost of 5 jackets and 4 shirts. (3 marks)
(2J + 3S = 1800)8
(7.2J + 2.4S = 4800)10
16J + 24S = 14400
72J + 24S = 48000
56J = 33600
= 600
shrt = 1800 - 1600 = 200
3
1.2 x 600 = 720
1.2 x 200 = 240
5 x 720 + 4 x 240
3600 + 960
= 4560 - Without using mathematical tables evaluate
 (3marks)
(3marks)
- Using a ruler and a pair of compass only, construct a rhombus ABCD such that AC = 10 cm and ∠BAD = 60° (3marks)
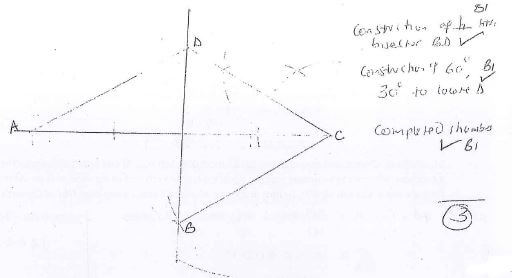
- Without using a calculator or mathematical tables, evaluate
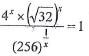 (3marks)
(3marks)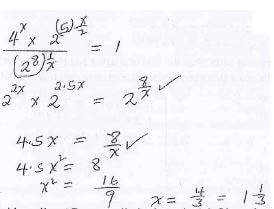
- A point P divides a line AB externally in the ratio 4:3. Given that A is (-2, 4) and point B (2,-3). Find the coordinates of T. (3marks)
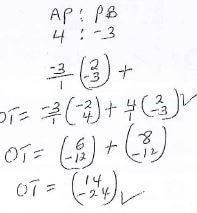
T(14, -24)
SECTION II (50MARKS)
Answer only five questions from this section.
- In the figure below, AC=14 cm, AD = 16 cm, DC = 11 cm, and B is a point on AC

- Calculate, correct to 2d.p
- ∠BAD (3marks)
112 = 142+ 162 - 2 x 14 x 16 x cosA
121 = 196 + 256 - 448 cos A
448 cos A = 331
cos A = 0.7388
A = 42.37
- ∠BAD (3marks)
- The size of obtuse ∠ABD (3marks)
16/sin B = 12/sin 42.37
sin B = 0.8986
B = 63.97
obtuse angle B = 116.03
- Calculate correct to 1 decimal place:
- The length of AB (2marks)
ADB = 180 - (42.37 + 116.03)
= 21.6º
AB = 16
sin 21.6 sin 116.03
AB = 6.555
AB = 6.6 - The area of triangle BCD (2marks)
DBC = 180 - 116.03 = 63.97, BC = 14 - 6.555
= 7.445
1/2 x 7.445 x 12 x sin 63.97
40.14
40.1
- The length of AB (2marks)
- Calculate, correct to 2d.p
- The following table shows heights of 100 seedlings each measured to the nearest cm.
Height (cm) Frequency x fx cf frequency class 70 - 79 14 74.5 1043 14 1.4 80 - 84 16 82 1312 30 3.2 85 - 89 18 87 1566 48 3.6 90 - 94 20 92 1840 68 4.0 95 - 99 17 97 1649 85 3.4 100 - 109 15 104.5 1567.5 100 1.5 Σf = 100 Σfx = 89775 - Calculate the differences between the mean and the median. (6marks)
x = 8977.5 = 89.78
100
median = 89.5 + (50 - 48) x 5
20
= 89.5 + 0.5
= 90
differences = 90 - 89.78
= 0.22 - Draw a frequency polygon to illustrate the above information (4marks)
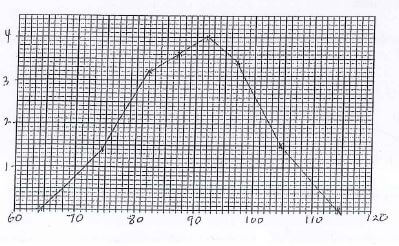
- Calculate the differences between the mean and the median. (6marks)
- Two towns P and Q are 280 km apart. A bus left town P at 9.30 am and travelled to Q at an average speed of 80 km/h. After 30 minutes, a car left town p for Q and travelled at an average speed of 100 km/h.
- Determine:
- The time when the car caught up with the bus. (3marks)
distance moved by bus
30/60 x 80 = 40 km
R.s = 100 - 80 = 20km/h
Time = 40/20 = 2hrs
9:30
2:00
11:30 am - The distance of the car from town Q when it overtook the bus. (3marks)
distance = 2 x 100 = 200 km
dixtance frm Q = 280 - 200
= 80 km
- The time when the car caught up with the bus. (3marks)
- After the car overtook the bus, it accelerated for 6 minutes to a speed of 120 km/h. It moved with that speed for 30 minutes after which breaks are applied and came to rest at town T after 3 minutes. Determine the distance travelled by the car in 39 minutes. (4marks)
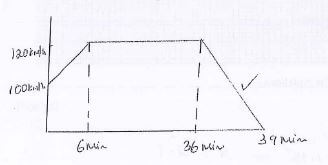
1/2 x 6/60(100 + 120) + 30/60 x 120 + 1/2 x 3/60 x 120
11 km + 60 km + 3 km
= 74 km
- Determine:
-
- Complete the table of values for the equation y .-2x2 + 3x + 6. (2 marks)
x -3 -2 -1 0 1 2 3 4 y -21 -8 1 6 7 4 -3 -14 - Use the values above to draw the graph of y = -2x2 + 3x + 6. (3marks)
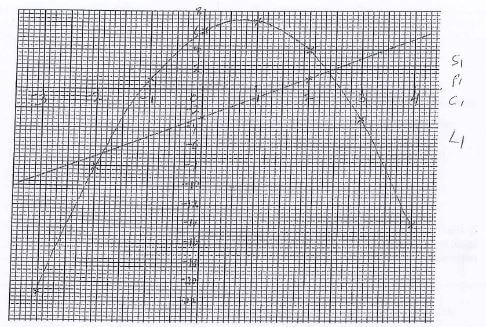
- Using the graph drawn above Solve the oquations:
- 2x2 = 3x +6 (2 marks)
-2x2 + 3x + 6 = 0
at point of intersection of curve with x-axis
x = -1.15 or x = 2.1 - -2x2 + x + 9 = 0 (3marks)
x = -1.85 or 2.35
- 2x2 = 3x +6 (2 marks)
- Complete the table of values for the equation y .-2x2 + 3x + 6. (2 marks)
- A trader deals with two types of Millet, type A and type B. type A costs ksh 400 per bag and type B costs ksh 350 per bag.
- The trader mixes 30 bags of type A and 50 bags of type B. If she sells the mixture at a profit of 20%, calculate the selling price of one bag of the mixture. (4 marks)
30 x 400 + 50 x 350
80
29500
80
368.75
100% - 368.75
120% - 120 x 368.75
100
= 442.50 - The trader now mixes type A and type B in the ratio x: y respectively. If the cost of the mixture is ksh 383.50 per bag, find the ratio x:y. (4marks)
400x + 350y = 383.50
x + y
400x + 350y = 383.50x + 383.50y
16.5x = 33.5y
x/y = 33.5/16.5
x/y = 21/33
x:y = 67:33 - The trader mixes one bag of the mixture in part (a) with one bag of the mixture in part (b) above. Calculate the ratio of type A millet to type B millet in this mixture. (2marks)
A:B = 3:5 A:B = 67:33
A 3/8 A 67/100
B 5/8 B 33/100
3/8 + 67/100 : 5/8 + 33/100
19/200 : 191/200
209/200: 191/200
209:191
- The trader mixes 30 bags of type A and 50 bags of type B. If she sells the mixture at a profit of 20%, calculate the selling price of one bag of the mixture. (4 marks)
- The equation of a line L1 is 3y + 2x = 10
- Find in form of y=mx+c,where m and care constants:
- The equation of line L2 passing through N (-5,2) and parallel to L1 (2 marks)
3y = -2x + 10
y = -2x/3 + 10/3
Q1 = -2/3 = a2
y - 2 = -2
x + 5 3
-2x - 10 = 3y - 6
-2x - 4 = 3y
y = -2x/3 - 4/3 - The equation of line L3 perpendicular to L2 at M (1,-8) (3marks)
y = 3/2x - 19/2
- The equation of line L2 passing through N (-5,2) and parallel to L1 (2 marks)
- Find the angle of inclination of the line L, with the horizontal. (2marks)
tan θ = -2/3
θ = 33.69
but tan is -ve
therefore θ = 146.3 - Find the magnitude of MN. (3marks)
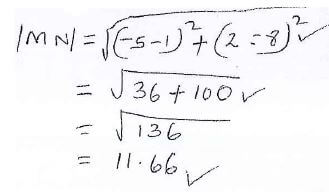
- Find in form of y=mx+c,where m and care constants:
- In the figure below A, B, C and D are points on the circle Centre O. ACF and EDFG are straight lines. Line EG is a tangent to the circle at D. ∠CDF = 35° and ∠CFG = 130°

- Calculate the Size of
- ∠OCD (2 marks)
1/2(180 - 70) = 55º - ∠EDA (1 mark)
ACD = EDA = 30 + 55 = 85º - ∠ABC (2 marks)
∠ ADC = 55 + 5 = 60º
∠ABC = 180 - 60 = 120º
- ∠OCD (2 marks)
- Given that CFo 6.7 cm and DF = 8.5 cm, Calculate to 3 significant figures:
- The length of DC. (3marks)
DC2 = 8.52 + 6.72 - 2 x 6.7 x 8.5 x cos 50
= √43.93
= 6.628
= 6.63 - The radius of the circle. (3marks)
r = 5.78
- The length of DC. (3marks)
- Calculate the Size of
- The product of the first three terms of a geometric progression is 64.If the first term is a and the common ratio is r,
- Express r in terms of a. (3marks)
- Given that the sum of the three terms is 14
- Find the value of a and r and hence write down two possible sequence up to the 4th term. (5 marks)
- Find the product of the 50th terms of the two sequence. (2marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Mangu High School Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
