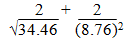MATHEMATICS PAPER 1 - KCSE 2019 MOKASA PRE MOCK EXAMINATION

SECTION I (50 marks)
Answer all the questions in section I

1. Without using calculators or mathematical tables, evaluate leaving your answer in standard form: (3 marks)
   5 x 6 – 76 ÷ 4 + 27 ÷ 3
      4 – 2 x 4 + 36 ÷ 4

2. Use squares, square roots and reciprocals tables to evaluate the following giving your answer to 2 decimal places. (3 marks)
   

3. Find the value of x in the following; 64^x+1 + 8^2x = 1040                                        (4 marks)

4. In a certain commercial bank, customers may withdraw cash through one of the two tellers at the counter. On average, teller 1 takes 3 minutes while teller 2 takes 5 minutes to serve a customer. If the two tellers start to serve customers at the same time, find the shortest time it takes to serve 100 customers. (3 marks)

5. A man standing 20m away from the foot of a vertical pole observes the top of the pole at an angle of elevation of 30°. He begins to walk along a straight line on level ground towards the pole. Calculate how far he walked before the angle of elevation of the pole becomes 80°.                    (3 marks)

6. Solve the following linear inequalities and represent the solution on a number line
   3x + 1˃ 10                                                                                         (3 marks)
   2(x-1) ˃ 8x – 32

7. A line AB = 10cm. By using another line, divide line AB into seven equal parts. (2 marks)

8. A group of 5 people can do a piece of work in 6 hours. Calculate at half the rate of the first group would take to complete the same work (3 marks)

9. The sum of the interior angles of a regular polygon is 4140°. Determine;
   1. The number of sides the polygon has                                                                   (2 marks)
   2. The size of each exterior angle the polygon has.                                                            (2 marks)

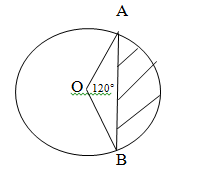
10. In the figure below, O is the centre of the circle of radius 2.8cm. Angle AOB = 120°. Determine the shaded area. (3 marks)
    

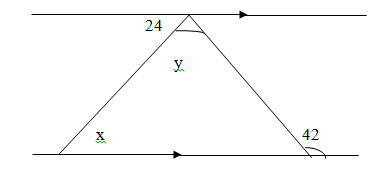
11. Use the figure below to solve the marked angles X, Y and Z (3 marks)
    

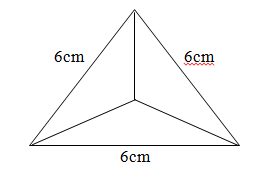
12. The figure below shows a solid regular tetra pack of sides 6cm.
    
    
    1. Sketch the net of the solid (1 mark)
    2. Find the surface area of the solid (2 marks)

13. A two digit number is such that the unit digit exceeds the tens digit by 5. If the digits are interchanged, the new number exceeds the original number by 45. Find the original number.
    (3 marks)

14. Two similar solids have masses of 80kg and 270kg. Find the surface area of the larger solid if the smaller solid has a surface area of 48cm³ (3 marks)

15. A Kenyan bank buys and sells foreign currencies at the exchange rates shown below.
                                                             Buying (Kshs)                       Selling (Kshs)
    1 Euro                                                148.56                                        149.00
    1 US Dollar                                          94.22                                          94.50
    An American arrived in Kenya with 20,000 Euros. He converted all the Euros into Kenyan shillings at the bank. He spent Kshs. 2,510,200 while in Kenya and converted the remaining Kenya shillings into U.S Dollars at the bank. Find the amount in dollars that he received.(4 marks)

16. Simplify:
     3x² – 2xy – y²                                                                                   (3 marks)
        9x² – y²                                             

SECTION II: (50 Marks)
Answer only FIVE questions from this section

17. Given that y = 7 – 3x – 2x2 for -4˂ x ˂ 3
    1. Complete the table below                                                                                       (2 marks)
       

       x	-4	-3	-2	-1	0	1	2	3
       7	7	7		7	7	7		7
       -3x	12	9		3	0	-3		-9
       -2x2	-32	-18		-2	0	-2		-18
       y	-13	-2		8	7	2		-20

                  
    2. Draw the graph y = 3x – 2x² for -4˂ x ˂ 3
    3. Use the graph to find the roots of the equation.
       1. -2x² – 3x + 7 = 0 (2 marks)
       2. -2x² – 4x – 9 = 0 (3 marks)

18. PQRS is a parallelogram whose two vertices are P(1,2) and R(6,4). PS is parallel to the line L₁ which cuts y-axis at 5 and passes through (-2,3)
    1. Find the equation of line PS (2 marks)
    2. Find the coordinates of S (3 marks)
    3. Find the coordinates of Q (2 mark
    4. Find the equation of line L2 which is perpendicular bisector of line QR (2 marks)

19. A particle moves along a straight line such that its displacement S metres from a given point is S = 2t³ – 4t² + 2t + 6 where t is time in seconds. Find;
    1. The displacement of the particle at t = 3 (2 marks
    2. The velocity of the particle when t = 5 (3 marks)
    3. The values of t when the particle is momentarily at rest (3 marks)
    4. The acceleration of the particle when t = 2 (2 marks)

20.  
    1. On the grid provided draw the square whose vertices are A(6,-2) B(7,-2) C(7,-1) D(6,-1)  (1 mark)
    2. On the same grid, draw:
       1. A¹B¹C¹D¹, the image of ABCD, under an enlargement scale factor 3, centre (9,-4) 
       2. A¹¹B¹¹C¹¹D¹¹, the image of A¹B¹C¹D¹ under reflection in the line x=0 (2 marks)
       3. A¹¹¹B¹¹¹C¹¹¹D¹¹¹ the image of A¹¹B¹¹C¹¹D¹¹ under rotation of +90° about (0,0) (2 marks)
    3. Describe a single transformation that maps A¹B¹C¹D¹ onto A¹¹¹B¹¹¹C¹¹¹D¹¹¹           (2 marks)

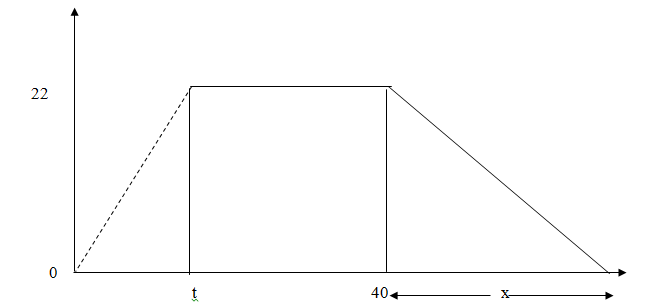
21. The figure below shows a velocity-time of journey of a car. The car starts from rest and accelerates at 2¾m/s² for t seconds until it is 22m/s.
    
    Brakes are applied bringing it uniformly to rest. The total journey is 847m long, find:
    1. The value of t, the acceleration time (2 marks)
    2. The distance travelled during the first t seconds. (2 marks)
    3. The value of x, the deceleration time (4 marks)
    4. The rate of deceleration (2 marks)

22. A garden measures 10m and 8m wide. A path of uniform width is made all round the garden. The total area of the garden and the path is 168m²
    1. Find the width of the path                                                                                       (4 marks)
    2. The path is to be covered with square concrete slabs. Each corner of the path is covered with a slab whose side is equal to the width of the path. The rest of the path is covered with slabs of side 50cm. the cost of making each corner slab is sh. 600 while the cost of making each smaller slab is sh. 50. Calculate;
       1. The number of the smaller slabs used.                                                     (3 marks)
       2. The total cost of the slabs used to cover the whole path                                   (3 marks)

23. The table below shows the height in cm of 100 mango trees.
    

    Height cm	15-19	20-24	25-29	30-34	35-39	30-44	45-49
    No. of trees	2	4	16	18	30	25	6

    1. On the grid provided and on the same axes represent the above data using;
       1. A histogram (4 marks)
       2. A frequency polygon (1 mark)
    2.  
       1. State the class in which the median height lies                                                   (1 mark)
       2. Using the histogram above, determine the number of trees whose height is 42cm or less

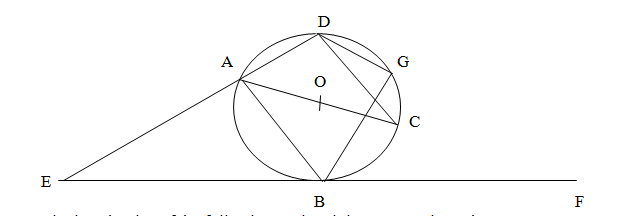
24. In the figure below AOC is a diameter of the circle centre O. AB = BC and ˂ACD = 35°, EBF is a tangent to the circle at B. G is a point on minor arc CD.
    
    Calculate the size of the following angles giving reasons in each case.
    1. ˂BCD (2 marks)
    2. Obtuse angle BOD (2 marks)
    3. ˂BAD                                                 (2 marks)
    4. ˂CGD (2 marks)
    5. ˂AEB (2 marks)