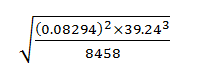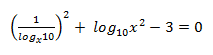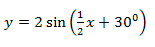MATHEMATICS PAPER 2 - KCSE 2019 MOKASA PRE MOCK EXAMINATION

SECTION A (50 MARKS)
Answer all questions in this section in the spaces provided

1. Use logarithms to evaluate.         (4 marks) 
          

2. Given that Find the values of a, b and c.      (3 marks)

3. Use completing square method to solve.                                                  (3 marks)
   2x²+5x=-3
   

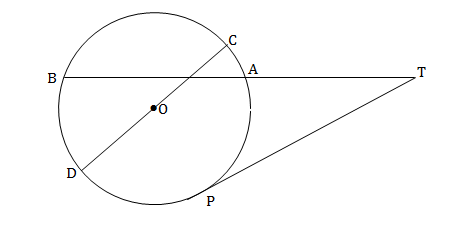
4. In the figure below O is the centre of the circle.  DC is diameter chord BA and DC intersect at R and TP is a tangent.  AT = 8cm, PT = 12cm and OD = 8cm.  
   
   

   Find the length of: BA   (2 marks)     

5. The equation of curve;Find the equation of the tangent to the curve at point x = 1.                                    (3 marks)

7. A quantity M is partly constant and partly varies as the cube root of N.  If M = 24.5 when N = 64 and M = 18.5 when N = 27; Find the constants and determine equation connecting M and N.     (4 marks)

8. Draw a line PQ = 4 cm.  Indicate by shading the region within which a variable point must lie if PA≤3cm and PA>AQ.(3 marks)

9. Solve using matrix method.(4 marks) 
   2x+3y=23
   x+5y  =29

10. Given that , make p subject of the formula.                                          (3 marks)

11. Find the area under curve y=x²+2 , between x = 2 and x = 6 by trapezium rule sing 4 strips.             (3 marks)

12. Solve for ϑ in the equation.         (4 marks)
    Sin(2θ-10)=-0.5 for 0⁰≤θ≤360⁰

13. Solve the equation:                                                                                                   (3 marks)
               

14. State the amplitude, period and phase angle of 
    1. Amplitude                                                                                                      (1 mark)
    2. Period                                                                                                             (1 mark)
    3. Phase angle                                                                                                   (1 mark)

15. Obtain the centre and radius of the circle represented by the equation.           (3 marks)
    x²+y²-10y+16=0       

16.  
    1. Use binomial expansion to expand (2+3/x)⁵up to the fourth term.       (2 marks)
    2. Use the expansion above to evaluate: (9.5)⁵                                            (2 marks)

SECTION B (50 MARKS)
Answer any five questions in this section

17. Two towns P and Q lie on the same parallel latitude such that P is due east of Q.  When local time at Q is 9.50 am, the local time at P is 3.12 pm. 
    1. Find the latitude difference between P and Q.                                          (2 marks)
    2. Give that the longitude of P is 52⁰E, find the longitude of Q.                  (2 marks)
    3. A pilot took off from town Q and flew to town P along the parallel of latitude.  The pilot took 3 ¼ hours travelling at an average speed of 860km/h to reach P.  Calculate to 1 d.p the latitude of town P and Q if they both lie in the northern hemisphere.                                                                                                     (3 marks)
    4. Two towns R and S are both on the equator and 3820nm apart.  Town R is due west of town S.  Find the local time at R when the local time at S is 2.20 pm. (Take R = 6370km and π= 22/7 )                                                              (3 marks)

18. In the figure below OA = a and OB=b, M is the mid-point of OA and AN:NB= 2 : 1.
    
    
    1. Express in terms of a and b.
       1. BA                                                                                                       (1 mark)
       2. BN                                                                                                      (1 mark)
       3. ON                                                                                                      (2 marks)
    2. Given that BX = hBM and OX = kON, determine the values of h and k.                                                                                                                                                (6 marks)

19. The table below shows Kenya Tax Rates in a certain year.
    The table below shows the payable tax.
    

    Income in (K£ per annum)	Tax rates(Ksh. Per £)
    1 – 4512	2
    4513 – 9,024	3
    9,025 – 13,536	4
    13,537 – 18,048	5
    18,049 – 22,560	6
    Over 22,560	6.5

    
    In that year Muhando earned a salary of Ksh. 16,510 per month.  He was entitled to a monthly tax relief of Ksh. 960.
    Calculate:
    1. Muhando’s annual salary in K£.                                                                  (2 marks)
    2. The monthly tax paid by Muhando in Ksh.                                                (6 marks)
    3. Find her net pay in Ksh.                                                                                (2 marks)

20. A box contains 3 brown, 9 pink and 15 white cloth pegs.  The pegs are identical except for the colour. 
    1. Find the probability of picking.                                                                  
       1. A brown peg.                                              (1 mark)            
       2. A pink or a white peg.                                    (2 marks)
    2. Two pegs are picked at random, one at a time without replacement.  Find the probability that:
       1. both are brown pegs.                                                  (3 marks)
       2. both pegs are of the same colour.                                      (4 marks)
21. The first, fifth and seventh terms of an arithmetic progression (AP) correspond to the first three consecutive terms of a decreasing Geometric Progression (GP). The first term of each progression is 64, common difference of the AP is d and the common ratio of the G.P is r.
    1. Write term equations involving d and r.                                                   (2 marks)
    2. Find the values of d and r.                                                                           (4 marks)
    3. Find the sum of the first 10 terms of:                                                        
       1. the Arithmetic Progression (AP) (2 marks)
       2. the Geometric Progression (GP) (2 marks)
22. The quantities P and Q are connected by the equation P=kRⁿ. The table below shows values of P and R.
    

    P	1.2	1.5	2.0	2.5	3.5	4.5
    R	1.6	2.3	3.4	4.7	7.9	11.5

              
    1. State the linear equation connecting P and R.                                           (1 mark)
    2. Using a scale of 2cm rep. 0.1 units on the y-axis and 1cm rep. 0.1 units on the x-axis; Draw a suitable line graph on the grid provided.                         (5 marks)
    3. From the graph you have drawn, estimate the values of;
       1. n (2 marks)
       2. k (1 mark)
    4. Find the linear law connecting P and R.                                                     (1 mark)
23.  
    1. Determine the stationary points of the curve; y=x³-3x²-9x+2
    2. Sketch the given curve above.                                                                     (4 marks)
24. The dimensions of a rectangular floor are such that:
    • the length is greater than the width but utmost twice the width.
    • the sum of width and length is more than 8m but less than 20m. If x represents the width and y the length.
      1. Write the inequalities to represent the above information.                     (4 marks)
      2.  
         1. Represent the inequalities on the grid below.                               (4 marks)
         2. Using the integral values of x and y, find the maximum possible area of the floor.     (2 marks)