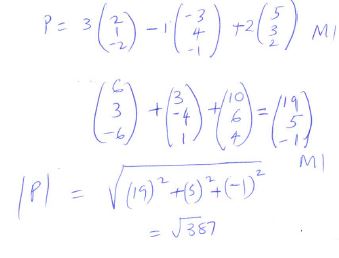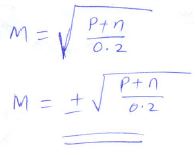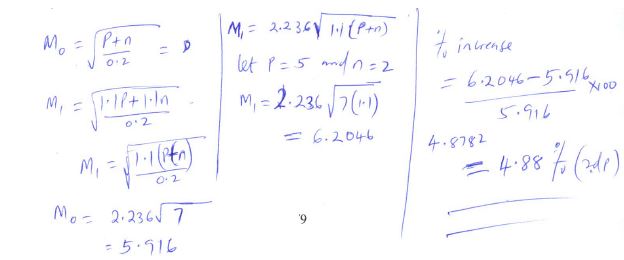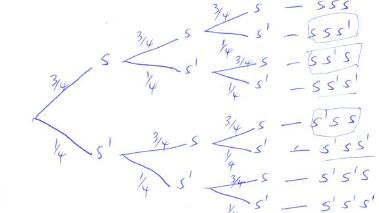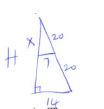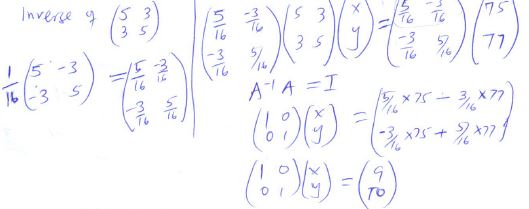Mathematics Paper 2 Pre Mock Questions and Answers - Mokasa I Joint Examination July 2021

INSTRUCTIONS TO THE CANDIDATES

• Write your name and school and index number in the spaces provided above
• This paper contains two sections; Section 1 and Section 11.
• Answer all the questions in section 1 and only five questions from Section 11
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-Programmable silent calculators and KNEC Mathematical tables may be used EXCEPT where stated otherwise.

FOR EXAMINERS’S USE ONLY
Section 1

Section 1I

QUESTIONS

SECTION I (50 marks):
Answer all questions in this section

1. Use logarithm tables to evaluate ( 4 marks)
2. Solve the equation 6^2x+1 = 2^3x+1 ( 3 marks)
3. Kevin truncated 0.00627 to 3 decimals and 487.74 to 3 significant figures. Calculate his percentage error in calculating product of numbers in truncated values to 1 decimal places. ( 3marks)
4. A new laptop depreciates at 8% per annum in the first year and 12% per year in the second year. If its value at the end of the second year was sh121,440. Calculate the original value of the laptop. (3marks)
5. Rationalize the denominator and simplify 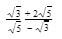( 3 marks)
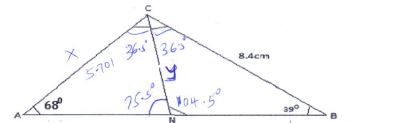
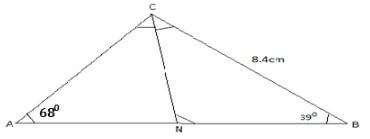
6. In the figure below angle A=68º, B= 390, BC= 8.4cm and CN is the bisector of angle ACB. Calculate the length CN to 1decimal place. ( 3 marks)
   
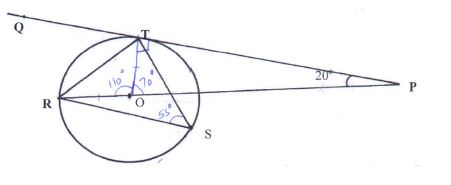
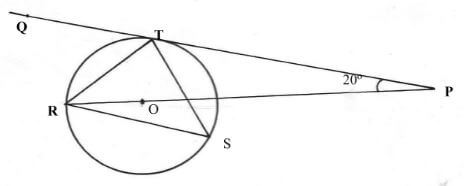
7. In the figure below R, T and S are points on a circle centre O. PQ is a tangent to the circle at T, POR is a straight line and angle QPR =20º. Find the size of angle RST (3marks)
   
8. Use binomial expansion to find the value of (1.02)5 correct to 3 decimal place. ( 4 marks)
9. Make x the subject of the equation (3 marks)
   
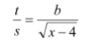
10. The equation of the circle is given by x² + y² + 8x -2y -1 = 0 . Determine the radius and the centre of the circle. (3marks)
11. Given that the minor arc of a circle subtends an angle of 140º at the centre of a circle of radii 3.5cm. Calculate the area of the major segment correct to 4 significant figures ( 3 marks)
12. Given that the matrix 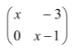is a singular matrix, find the values of x. (3marks)
13. The mass of a mixture A of peas and millet is 72 kg. The ratio of peas to millet is 3:5 respectively;
    1. Find the mass of millet in the mixture. (1mark)
    2. A second mixture of B of peas and millet of mass 98 kg is mixed with A. The final ratio of peas to millet is 8:9 respectively. Find the ratio of peas to millet in B (2marks)
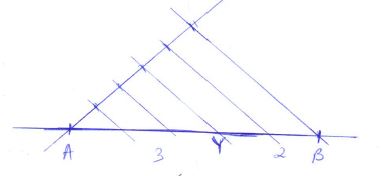
14. Draw a line AB= 8cm long. Divide the line proportionally into5 equal parts. Locate a point Y on the line AB such that AY: YB = 3:2. ( 3 marks)
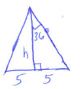
15. A solid prism is made of a pentagonal cross section of sides 10cm. If the prism is 30cm long calculate area of the cross section hence the volume of the prism (3 marks)
16. Given that X = 2i + j -2k, y = -3i + 4j – k and z= 5i + 3j + 2k and that p= 3x – y + 2z, find the magnitude of vector p to 3 significant figures. (3marks)
    
    
    

SECTION II (50 Marks)
Answer any five questions in this section

17. The masses in kilograms of patients who attended a clinic on a certain day were recorded as:
    38 52 46 48 60 59 62 73 49 54 49 41 57 58 69 72 60 58 42 41
    79 62 58 67 54 60 65 61 48 47 69 59 70 52 63 58 59 49 51 44
    67 49 51 58 54 59 39 59 54 52
    1. starting with class 35-39, make a frequency distribution table for the data indicating the class and frequency. ( 3 marks)
    2. state the modal class ( 1 mark)
    3. Calculate the mean mass ( 3 marks)
    4. Calculate the median mass ( 3 marks)
18. The income tax rates of a certain year were as shown below:
    

    Monthly taxable income in Ksh	Tax rate in %
    0-9680	10
    9681-18800	15
    8801-27920	20
    27921- 37040	25
    37041 and above	30

    
    In that year, Sayao monthly earnings were as follows; basic salary Ksh. 30 000, house allowance Ksh.15 000, and medical allowance of Ksh 3,500. He is entitled to a monthly tax relief of Ksh. 1056.
    1. Calculate Sayao’s taxable income ( 2 marks)
    2. Calculate his P.A.Y.E ( 5 marks)
    3. A part from P.A.Y.E, other deductions is education insurance policy Ksh. 1500 and Ksh 2500 as cooperative shares. Find his net income at end of the month. ( 3 marks)
19. A Quantity P varies partly as the square of m and partly as n. When p= 3.8, m = 2 and n = -3, When p = - 0.2, m = 3 and n= 2.
    1. Find
       1. The equation that connects p, m and n (4marks)
       2. The value of p when m = 10 and n = 4 (1mark)
    2. Express m in terms of p and n (2marks)
    3. If P and n are each increased by 10%, find the percentage increase in m correct to 2 decimal place. (3marks)
20.                    
    1. Complete the table below by filling in the blank spaces ( 2 marks)
       

       x	00	300	600	900	1200	1500	1800	2100	2400	2700	3000	3300	3600
       y=Cos x	1.00	0.87		0.00		1.00		-0.87				0.87
       y=3sinx	0.00			3.00								-1.50	0.00

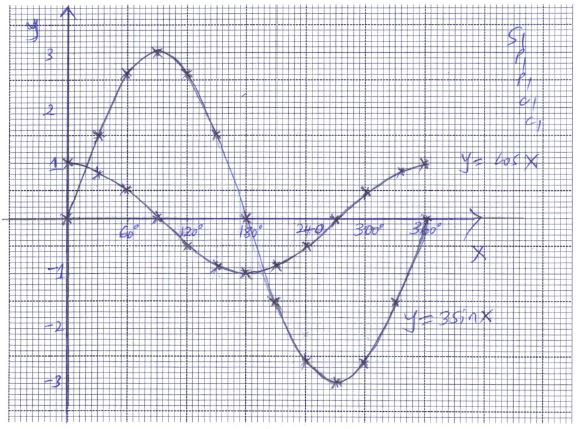
    2. using the scale 1cm to represent 30⁰ on the x-axis and 2 cm to represent 1 unit on the vertical axis, draw on the graphs of cosx and 3sinx ( 5 marks)
       
    3. use your graph to solve the equation cosx =3sinx ( 2 marks)
    4. What is the difference in the values of y=cosx and y=3sinx at x=120⁰ ( 1 mark)
21. The 5th term of an AP is 16 and the 12th term is 37.
    1. Find;
       1. The first term and the common difference ( 3 marks)
       2. The sum of the first 21 terms (2 marks)
    2. The second, fourth and the seventh term of an AP are the first 3 consecutive terms of a GP. If the common difference of the AP is 2.
       Find:
       1. The common ratio of the GP ( 3 marks)
       2. The sum of the first 8 terms of the GP (2 marks)
22. In driving to work, John has to pass through three sets of traffic lights. The probability that he will have to stop at any of the lights is ¾
    1. Draw a tree diagram to represent the above information. (2 marks)
    2. Using the diagram, determine the probability that on any one journey, he will have to stop at:
       1. All the three sets. (2 marks)
       2. Only one of the sets (2 marks)
       3. Only two of the sets (2 marks)
       4. None of the sets. (2 marks)
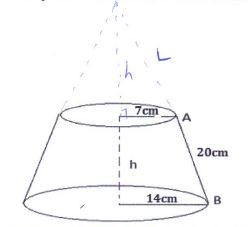
23. The figure below shows a lampshade in the form of a conical frustum
    
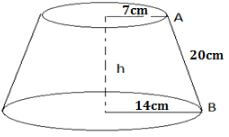
    The top and bottom radii are 7cm and 14cm respectively. The slant height AB is 20cm. Calculate:
    1. The slant height of the original cone correct to two decimal places ( 2 marks)
    2. The height h, of the lampshade ( 2 marks)
    3. The curved surface area of the lampshade ( 3 marks)
    4. The volume of the lampshade correct to 4 significant figures ( 3 marks)
24. Gary bought 5 tins of plums and 3 tins of peaches from a supermarket for Ksh.75, while Mike bought 3 tins of plums and 5 tins of peaches for Ksh.77
    1. Set up the simultaneous equations which represent the given information (2 marks)
    2. Write down the matrix equation ( 2 marks)
    3. Using the matrix method, find the cost of
       1. 4 tins of plums ( 5 marks)
       2. 2 tins of peaches ( 2 marks)

MARKING SCHEME

SECTION I (50 marks):
Answer all questions in this section

1. Use logarithm tables to evaluate ( 4 marks)
   
   

   No	Standard form	Log
   0.4239 149.6 log6 = 0.7782 4.332	4.239 × 10-1 1.496 × 102 7.782 × 10-1 4.335 × 10º	1.6272 + 2.1750 1.9022 - 1.8911 1.9111    3 0.6370	M1 M1 M1

   
   =4.335M
2. Solve the equation 6^2x+1 = 2^3x+1 ( 3 marks)
   (2x + 10)log6 = (3x + 1)LOG2
   2x + 1 = log2 M1
   3x + 1    log6
   2x + 1 = 0.3869
   3x + 1
   2x + 1 = (3x + 1)(0.3869) M1
   2x + 1 = 1.1607x + 0.3869
   2x - 1.1607x = 0.3869 - 1
   0.8393x =  -0.6131
   x = -0.7305 A1
3. Kevin truncated 0.00627 to 3 decimals and 487.74 to 3 significant figures. Calculate his percentage error in calculating product of numbers in truncated values to 1 decimal places. ( 3marks)
   Actual = 0.00627 × 487.74
   =3.0581298
   Truncated = 0.006 × 488 M1
   =2.928
   % = Actual - Truncated
                   Actual
   3.0581298 - 2.928
        3.0581298
   = 0.1301298 × 100
       3.0581298
   =4.255
   =4.3% 1dp  A1
4. A new laptop depreciates at 8% per annum in the first year and 12% per year in the second year. If its value at the end of the second year was sh121,440. Calculate the original value of the laptop. (3marks)
   Let the original value be P
   A = P(1 - ^r/₁₀₀)ⁿ
   P(1 - ⁸/₁₀₀)¹
   A = P(⁹²/₁₀₀)
   = 0.92P
   2nd year
   A = P(1 - ^r/₁₀₀)ⁿ
   0.92P(1 - ¹²/₁₀₀)¹
   0.92P(0.88)
   A = 0.8096P
   0.8096P = 121,440 M1
   P = 121,440
          0.8096
   P = shs.150,000 A1
5. Rationalize the denominator and simplify 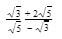( 3 marks)
   (√3 + 2√5)(√5 + √3)
     (√5 - √3)(√5 + √3)
   Numerator
   √3(√5 + √3) +2√5(√5 + √3)
   √15 + 3 + 10 + 2√15
   13 + 3√15  M1
   Denominator
   (√5 - √3)(√5 + √3)
   5 - 3 = 2 M1
   13 + 3√15
         2
   6.5 + 1.5√15    A1
6. In the figure below angle A=68º, B= 390, BC= 8.4cm and CN is the bisector of angle ACB. Calculate the length CN to 1decimal place. ( 3 marks)
   
   ACN = 180º - (68 + 39) = 365º
                      2
     8.4   =    x    
   sin68º   sin39º
   x =    8.4    × sin39º = 5.701
          sin68º
      CN    =  5.701   
     sin68     sin75.5
   cn = 5.701 × sin68
          sin75.5
   CN = 5.459
   CN = 5.5(1dp) cm
7. In the figure below R, T and S are points on a circle centre O. PQ is a tangent to the circle at T, POR is a straight line and angle QPR =20º. Find the size of angle RST (3marks)
   
   RST = 55º
   Angle substended by a chord at the centre is thrice what is substends at the circumference
8. Use binomial expansion to find the value of (1.02)5 correct to 3 decimal place. ( 4 marks)
   (1 + x)⁵ = 1⁵(x)⁰ + 1⁴(x)¹ + 1³(x)² + 1²(x)³ + 1¹(x)⁴ + 1⁰(x)⁵ 
   x = 0.02
   1 + x + x² + x³ + x⁴ + x⁵
   1    5    10   10    5        1
   1 + 5x + 10x² + 10x³ + 5x⁴ + x⁵ M1
   1 + 5(0.02) + 10(0.02)² + 10(0.02)³ + 5(0.02)⁴ + (0.02)⁵  M1
   1 + 0.1 + 0.004 + 0.00008 + 0.0000008 + 0.0000000032 M1
   = 1.1040808
   = 1.104(3 dp) A1
9. Make x the subject of the equation (3 marks)
   
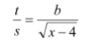
   (^t/_s)² = (^b/_{√x - 4})²
   t² =   b²
   s²   (x - 4)
   t²(x - 4) = s²b²
   t²x - 4t² = s²b²
   t²x = s²b² + 4t² M1
   x = s²b² + 4t²   A1
              t²   
10. The equation of the circle is given by x² + y² + 8x -2y -1 = 0 . Determine the radius and the centre of the circle. (3marks)
    x² + 8x + 16 + y² - 2y + 1 = 1 + 16 + 1
    (x + 4)² + (y - 1)² = 18
    Centre (-4,1)  radius = √18 = 4.243 units
11. Given that the minor arc of a circle subtends an angle of 140º at the centre of a circle of radii 3.5cm. Calculate the area of the major segment correct to 4 significant figures ( 3 marks)
    360 - 140 = 220
    220 x 22 x 3.5² = 23.52778
    360    7
    = 23.53 cm²
12. Given that the matrix 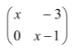 is a singular matrix, find the values of x. (3marks)
    x( x- 1) - 0 = 0
    x² - 1 = 0
    x² = 1 
    x = √1
    x = 1  or x = -1
    x = ±1
13. The mass of a mixture A of peas and millet is 72 kg. The ratio of peas to millet is 3:5 respectively;
    1. Find the mass of millet in the mixture. (1mark)
       Total mass = 72 kg
       peas: millet
       3:5
       a) millet = ⁵/₈ x 72 = 45kg
    2. A second mixture of B of peas and millet of mass 98 kg is mixed with A. The final ratio of peas to millet is 8:9 respectively. Find the ratio of peas to millet in B (2marks)
       A + B mixture = 72 + 98 = 170 kg
       mass of peas in A  = ³/₈ x 72 = 27kg
       A and B 8:9 of 170 kg
       peas = 8/17 x 170 = 80kg
       millet 9/17 x 170 = 90kg
       In mixture 
       B:millet = 90 - 45
       =45kg
       In mixture
       B :peas 
       =80 - 27
       =53kg
       Ratio = 53:45
14. Draw a line AB= 8cm long. Divide the line proportionally into5 equal parts. Locate a point Y on the line AB such that AY: YB = 3:2. ( 3 marks)
    
15. A solid prism is made of a pentagonal cross section of sides 10cm. If the prism is 30cm long calculate area of the cross section hence the volume of the prism (3 marks)
    
    tan36º = 5
                  h
    h =     5    
          tan36º
    h = 6.882
    5(¹/₂ x 6.882 x 10) 
    cross sectionesd are = 172.05cm²
16. Given that X = 2i + j -2k, y = -3i + 4j – k and z= 5i + 3j + 2k and that p= 3x – y + 2z, find the magnitude of vector p to 3 significant figures. (3marks)
    
    = 19.7

SECTION II (50 Marks)
Answer any five questions in this section

17. The masses in kilograms of patients who attended a clinic on a certain day were recorded as:
    38 52 46 48 60 59 62 73 49 54 49 41 57 58 69 72 60 58 42 41
    79 62 58 67 54 60 65 61 48 47 69 59 70 52 63 58 59 49 51 44
    67 49 51 58 54 59 39 59 54 52
    1. starting with class 35-39, make a frequency distribution table for the data indicating the class and frequency. ( 3 marks)
       

       class	tally	frequency	x	fx	c.f
       35-39	ll	2	37	74	2
       40-44	llll	4	42	168	6
       45-49	llll lll	8	47	376	14
       50-54	llll llll	9	52	468	23
       55-59	llll llll l	11	57	627	34
       60-64	llll ll	7	62	434	41
       65-69	llll	5	67	335	46
       70-74	lll	3	72	216	49
       75-79	l	1	77	77	50
       				Σfx = 2775

    2. state the modal class ( 1 mark)
       55 - 59
    3. Calculate the mean mass ( 3 marks)
       mean = Σfx = 2775
                              50
       = 55.5
    4. Calculate the median mass ( 3 marks)
       54.5 + 2 x 5 = 55.41
                11
18. The income tax rates of a certain year were as shown below:
    

    Monthly taxable income in Ksh	Tax rate in %
    0-9680	10
    9681-18800	15
    8801-27920	20
    27921- 37040	25
    37041 and above	30

    In that year, Sayao monthly earnings were as follows; basic salary Ksh. 30 000, house allowance Ksh.15 000, and medical allowance of Ksh 3,500. He is entitled to a monthly tax relief of Ksh. 1056.
    1. Calculate Sayao’s taxable income ( 2 marks)
       30,000 + 15,000 + 3,500 = 48,500
    2. Calculate his P.A.Y.E ( 5 marks)
       9680 × 10 = 968
                  100
       9120 × 15= 1368
                  100
       9120 × 20 = 1824
                  100
       9120 × 25= 2280
                  100
       11460 × 30 = 3438
                    100
       Gross tax = 9878
       P.A.Y.E = 9878 - 1056
       = ksh. 8822 p.m
    3. A part from P.A.Y.E, other deductions is education insurance policy Ksh. 1500 and Ksh 2500 as cooperative shares. Find his net income at end of the month. ( 3 marks)
       Total deductions = 8822 + 2500 + 1500
       = 12, 822
       Net income = 48,500 - 12,822 = ksh. 35,678
19. A Quantity P varies partly as the square of m and partly as n. When p= 3.8, m = 2 and n = -3, When p = - 0.2, m = 3 and n= 2.
    1. Find
       1. The equation that connects p, m and n (4marks)
          p = xm² + yn
          3.8 = 4x - 3y
          -0.2 = 9x + 2y
            7.6 = 8x - 6y
          -0.6 = 27 + 6y  +
             7 = 35x
          x = ⁷/₃₅ = ¹/₅ = 0.2
          3.8 = 0.8 - 3y
          3 = =-3y
          y = -1
          P = 0.2m² - n
       2. The value of p when m = 10 and n = 4 (1mark)
          P= 0.2 x 100 - 4
          =20 - 4
          =16
    2. Express m in terms of p and n (2marks)
       P = 0.2m² - n
       0.2m² = P + n
       m² = p + n
                 0.2
       
    3. If P and n are each increased by 10%, find the percentage increase in m correct to 2 decimal place. (3marks)
       
20.                    
    1. Complete the table below by filling in the blank spaces ( 2 marks)
       

       x	00	300	600	900	1200	1500	1800	2100	2400	2700	3000	3300	3600
       y=Cos x	1.00	0.87	0.50	0.00	-0.50	-0.89	-1.00	-0.87	0.50	0.00	0.50	0.87	1.00
       y=3sinx	0.00	1.50	2.60	3.00	2.60	1.50	0.00	-1.50	-2.60	3.00	-2.60	-1.50	0.00

    2. using the scale 1cm to represent 30⁰ on the x-axis and 2 cm to represent 1 unit on the vertical axis, draw on the graphs of cosx and 3sinx ( 5 marks)
       
    3. use your graph to solve the equation cosx =3sinx ( 2 marks)
       x = 18º, 198º
    4. What is the difference in the values of y=cosx and y=3sinx at x=120⁰ ( 1 mark)
       2.60 - - 0.5 = 3.1 
21. The 5th term of an AP is 16 and the 12th term is 37.
    1. Find;
       1. The first term and the common difference ( 3 marks)
          T_n = a + (n - 1)d
          T₅ = a + 4d = 16
          T₁₂ = a + 11d = 37 
            7d = 21
          d = 3
          a + 4 (3) = 16
          a + 12 = 16
          a = 4
       2. The sum of the first 21 terms (2 marks)
          S₂₁ = 21 {2(4) + 20(3)}
                   2
          = 714
    2. The second, fourth and the seventh term of an AP are the first 3 consecutive terms of a GP. If the common difference of the AP is 2.
       Find:
       1. The common ratio of the GP ( 3 marks)
          a + d, a + 3d, a + 6d
          a + 2  a + 6  a + 12
          a + 6 = a + 12
          a + 2    a + 6
          (a + b)² = (a + 2)(a + 12)
          a + 12a + 36 = a² + 14a + 24
          12= 2a
          a = 6
          comm ratio
          r = 12 = 11
                8       2
       2. The sum of the first 8 terms of the GP (2 marks)
          S₈ = 8((³/₂)8 - 1 ) = 197.03 = 394.063
                       1¹/₂ -1           ¹/₂
22. In driving to work, John has to pass through three sets of traffic lights. The probability that he will have to stop at any of the lights is ¾
    1. Draw a tree diagram to represent the above information. (2 marks)
       
    2. Using the diagram, determine the probability that on any one journey, he will have to stop at:
       1. All the three sets. (2 marks)
          P(sss) = ³/₄ × ³/₄ × ³/₄ = ²⁷/₆₄
       2. Only one of the sets (2 marks)
          P(ss¹s¹) or P(s¹ss¹) or P(s¹s¹s)
          (³/₄ × ¹/₄ × ¹/₄) + (¹/₄ × ³/₄ × ¹/₄) + (¹/₄ × ¹/₄ × ³/₄) = ³/₆₄  × 3 = ⁹/₆₄
       3. Only two of the sets (2 marks)
          P(sss¹) or P(ss¹s) or P(s¹ss) 
          (³/₄ × ³/₄ × ¹/₄) + (³/₄ × ¹/₄ × ³/₄) + (¹/₄ × ³/₄ × ³/₄) = (⁹/₆₄)3 = ²⁷/₆₄
       4. None of the sets. (2 marks)
          P(s¹s¹s¹) = ¹/₄ × ¹/₄ × ¹/₄ = ¹/₆₄
23. The figure below shows a lampshade in the form of a conical frustum
    
    The top and bottom radii are 7cm and 14cm respectively. The slant height AB is 20cm. Calculate:
    1. The slant height of the original cone correct to two decimal places ( 2 marks)
       L + 20 = 14
           L         7 
       14L = 7L + 140
       7L = 140
       L = 20
       Slant height 
       = 20 + 20 = 40cm
    2. The height h, of the lampshade ( 2 marks)
       
       40² = H² + 14²
       1600 = H² + 196
       1600 - 196 = H²
       H² = 1404
       H = 37.47
       20² = X² + 49
       400 - 49 = X²   
       X = 18.73
       37.44 - 18.73
       h = 18.74cm
    3. The curved surface area of the lampshade ( 3 marks)
       T1R1 - T1rL
       ²²/₇ × 14 × 40  - ²²/₇ × 7 × 20
       1760 - 440 = 1320cm²
    4. The volume of the lampshade correct to 4 significant figures ( 3 marks)
       ¹/₃πR²H - ¹/₃πr²h
       ¹/₃ × ²²/₇ × 14² × 37.47  - ¹/₃ × ²²/₇ × 7² × 18.73
       = 7693.84 - 961.47
       = 6732.37cm³
24. Gary bought 5 tins of plums and 3 tins of peaches from a supermarket for Ksh.75, while Mike bought 3 tins of plums and 5 tins of peaches for Ksh.77
    1. Set up the simultaneous equations which represent the given information (2 marks)
       let plums be x and peaches be y
       5x + 3y = 75
       3x + 5y = ??
    2. Write down the matrix equation ( 2 marks)
       
    3. Using the matrix method, find the cost of
       1. 4 tins of plums ( 5 marks)
          
       2. 2 tins of peaches ( 2 marks)
          2 tins of peaches
          10 × 2 = 20
          IA = A
          x = 9 
          y   10
          x = 9
          y = 10
          4 tins of peaches  = 9 × 4 = ksh. 36