INSTRUCTIONS TO THE CANDIDATES
- Write your name and index number in the spaces provided above
- This paper contains two sections; Section A and Section B
- All workings and answers must be written on the question paper in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- This paper consists of 15 printed pages.
- Candidates should check carefully to ascertain that all the pages are printed as indicated and no questions are missing.
Section A. (50mks)
Answer all the questions in this section in the spaces provided.
- Without using a calculator evaluate. (3mks)
(21/3-11/5 of 4)
¼ - (-1/3)2 - Use logarithms to evaluate (4mks)
5√(0.0066283×193.9
2.2822 - Without using a calculator or mathematical tables evaluate. (3mks)
43⁄2 × (256/2401)¾ - The base of a right pyramid is a rectangle of length 80cm and width 60cm. each slant edge of the pyramid is 150cm. Calculate the volume of the pyramid. (3mks)
- Simply. (3mks)
2x2- xy - 6y 2
x2- 4xy + 4y2 - A two digit number is such that, the sum of its digits is 13. When the digits are interchanged the original number is increased by 9. Find the original number. (4mks)
- The size of an interior angle of a regular polygon is 3x0 while its exterior is (x+20)2. Find the number of triangles that makes the polygon. (3mks)
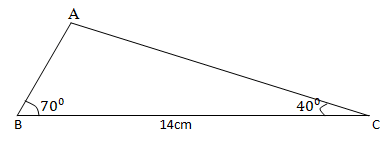
- In the triangle ABC below BC = 14cm <ABC= 70º and <ACB=40º. Calculate; correct to 4 significant figures the areas of triangle ABC. (3mks)
- A vector given by (2-4) transforms a point A(3,6) to A1. Find the distance A A1 (3mks)
-
- Using a rule and a pair of compasses only, construct a quadrilateral PQRS in which PQ = 6cm ,PS = 4cm QR = 5cm, <PQR=105º and <SPQ= 90º (2mks)
- The quadrilateral PQRS represents a plot of land drawn to a scale of 1:4000. Determine the actual length of RS in metres. (2mks)
- Without using mathematical tables or calculator evaluate. (3mks)
sin30º - sin60º
60º - Use matrix method to solve. (3mks)
5x+3y= 35
3x-4y= - 8 - Use mathematical tables to find the reciprocal of 0.0247, hence evaluate. (4mks)
∛3.025 Correct to 2 decimal places.
0.0247 - A Kenyan businessman intended to buy goods worth US dollar 20,000 from South Africa. Calculate the value of the goods to the nearest south Africa (S.A) Rand given that 1 US dollar = Ksh 101.9378 and 1 S.A Rand = Ksh 7.6326. (3mks)
- Find all integral values of x which satisfy the inequalities. (3mks)
5-3x ≤x-7 <11-2x - Express 5184 and 2744 in terms of its prime factors hence determine the value of
√5184 (4mks)
∛2744
Section B (50mks)
Answer any five questions from this section on the spaces provided. - Two vertices of a rectangle ABCD are A(3,6) and B( 7,12)
- Find the equation of line AB. (3mks)
- Find the equation of the perpendicular bisector of line AB. (4mks)
- Given that BC is perpendicular to AB. Find the equation of BC. (3mks)
- Three business partners Abila, Bwire and Chirchir contributed Ksh 120,000, Ksh 180,000 and Ksh 240,000 respectively to boost their business. They agreed to put 20% of the profit accrued back into the business and to use 35% of the profits for running the business. The remainder was to be shared among the business partners in the ratio of their contribution. At the end of the year, a gross profit of Ksh 225,000 was realised.
- Calculate the amount.
- Put back into the business. (2mks)
- Used for official operations. (1mk)
- Calculate the amount of profit each partner got. (4mks)
- If the amount put back into the business was added to individual’s shares proportionately of their initial contributions, find the amount of Chirchir’s new shares. (3mks)
- Calculate the amount.
- Coast bus left Nairobi at 8.00Am and travelled towards Mombasa at an average speed of 80Km/hr. At 8.300am Lamu bus left Mombasa towards Nairobi at an average speed of 120Km/hr. given that the distance between Nairobi and Mombasa is 400Km, determine.
- The time Lamu bus arrived in Nairobi. (2mks)
- The time the two buses met. (4mks)
- The distance from Nairobi to the point where the buses met. (2mks)
- How far coast bus is from Mombasa when Lamu bus arrives in Nairobi. (2mks)
- A land is enclosed by four straight boundaries AB,BC,CD and DA. Point B is 25Km on bearing of 315º from A, C is directly south of B on a bearing of 260º from A and D is 30Km on a bearing of 210º from C
- Using a scale of 1cm to represents 5Km represent the above information on a scale drawing. (3mks)
- Using the scale drawing, determine the
- Distance in Kilometres of D from A. (2mks)
- Bearing of A from D. (1mk)
- Calculate the area, correct to 1 decimal place, of the land in square kilometres. (4mks)
- Complete the table below for the functions
- y= x2- 6x+7 (2mks)
x 0 1 2 3 4 5 6 -x2 0 - - 9 16 25 - -6x - -6 -12 - - - -36 7 7 7 7 7 7 7 7 Y = x2 - 6x + 7 7 - -1 -2 - - - - On the grid provided below draw the graph of y= x2- 6x+7 for 0 ≤ x ≤6 and use it to estimate the roots of the equation.
x2- 6x+7=0 (4mks)
- Use the graph above to solve the equation x2- 7x+9=0 (3mks)
- Determine the range of values of X for which x2- 6x+7 <x-2 (1mk)
- y= x2- 6x+7 (2mks)
- In the figure below PQR and S are points on the circumference of the circle centre O. TP and TR are tangents to the circle at P and R respectively. POQ is a diameter of the circle and angle PQR = 64º (10mks)
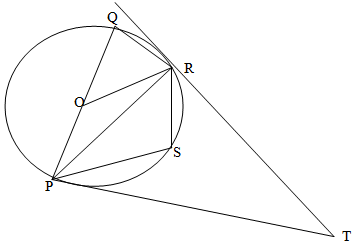
Giving reasons on each case, find the size of- <ROP
- <PSR
- <ORP
- <TRP
- <RTP
- The figure below shows two triangles ABC and BCD with a common base BC = 3,4cm. The area of triangle ABC = Area of triangle BCD and ABC =90º
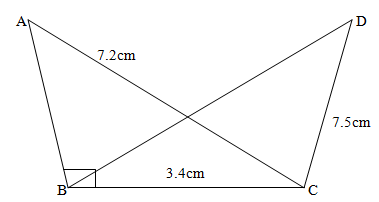
- Calculate, correct to one decimal place.
- The area of triangle ABC. (3mks)
- The size of <BCD (3mks)
- The length of BD (2mks)
- The size of <BDC (2mks)
- Calculate, correct to one decimal place.
- The marks scored by 40 students in a mathematics test were as shown in the table below.
Marks 48 – 52 53 – 57 58 – 62 63 – 67 68 – 72 73 – 77 Number of students 3 4 10 12 8 3 - State the modal class. (1mk)
- Using an assumed mean of 64, calculate the mean mark. (3mks)
- On the grid provided, draw the cumulative frequency curve for the data. (3mks)

- Use the graph to estimate the semi- interquartile range (3mks)

MARKING SCHEME
- 21/3 – 11/5o of 4
6/5 ×4= 24/5
7/3= -24/5= 35/15 - 72= -37/15
¼ - (-1/3)2
¼ - 1/9= 9 - 4 = 5
36 36
-37/15 × 36/5 = 1719/25
M1 for -37/15
M1 for 5/36
A1 for 1919/25 - No. std Log
0.006628 6.628×10-3 3 ̅ .8214
3
7 ̅ .4642
+
193.9 1.939×102 2.2876
5 ̅ .7518
2.2822 2.2822×10º 0.3584
5 ̅ .3934
5
0.1198 1.198×10-1 1 ̅.0.786
M1 for – correct logs
M1 for 5 ̅ .7518
M1 for 1 ̅.0.786
A1 for C.A - 49 3⁄2 = √493= 73=343
256 = ( ∜256 )3=64
2401= ( ∜2401)3=243
343 × 64/343=64
M1for 343
M1 for 64, 343
A1 for C.A 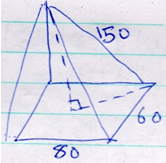
Length of diagonal
√(802 + 602=100
½ diagonal = 50
Height = 1502- 502
= 22500 – 2500
= 20000
=√20000=141.4
1/3×80 ×60 ×141.4
226. 2
M1 for height
M1 for expression of volume
A1 for C.A- 2x2 – xy – 6y2
2x2 – 4xy + 3xy – 6y2
2x (x-2y) + 3y( x-2y)
(2x+3y) (x – 2y)
x2- 4xy + 4y2
x2– 2xy – 2xy + 4y2
x(x-2y) – 2y( x-2y)
(x-2y) (x-2y)
(2x+3y)(x-2y)
(x-2y) (x-2y)
2x+3y
x-2y
M1 for (2x+3y) (x – 2y)
M1 for (x-2y) (x-2y)
A1 for C.A - x+y=13
(10y + x ) - ( 10x + y) = 9
10y + x – 10x – y = 9
9y – 9x = 9
y – x = 1
- x+ y = 13
-x + y = 1
2x = 12
y=6
x + y = 13
6 +y = 13
Y = 7
M1 for 9y – 9x = 9
M1 for 2x = 12
A1 for both values of x and y. - int+ext=180
3x + x + 20 = 180
4x + 20 = 180
4x +160
X = 40
Ext = 40 + 20 = 60
Ext = 360/n= 360/n=60
n=360/60=6
Number of triangles = n – 2
= 6- 2
= 4
M1 for expression
M1 for 360/60
A1 for C.A - <BAC=180-110
= 70º
14 = AC
sin70 sin70
AC = 14 × sin70
sin 70
AC = 14
Area = ½ ×14 14 × sin40
=62.99
=63.0
M1 for expression of AC
M1 for for expression of area
A1 for C.A - O+T =1
(36)+ (2-4)= (52)
Distance - √(52+ 22)
= 5.385
M1 for addition of vectors
M1 for for expression of distance
A1 for C.A 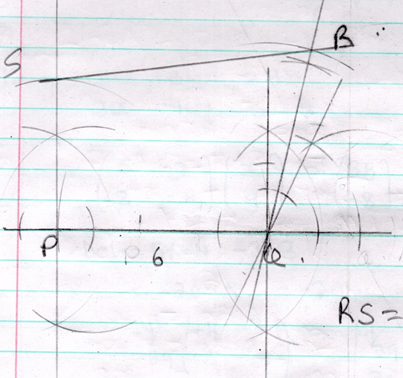
Rs = 7.cm
1: 4000
7.4: 7.4 ×4000
= 29600
B1 for PQR and SPQ
B1 for for complete figure
B1 for for RS
B1 for C.A- sin 30º - sin 6º
tan60º
Sin 30º=½ tan60º = √3
sin60º= √3/2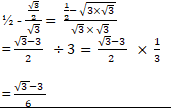
M1 for trigonometric ratio
M1 for for rationalising
A1 for C.A - 5x + 3y =38
3x – 4y = -8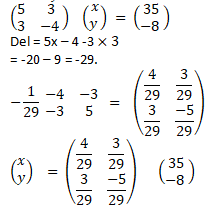
x=4 y=5
B1 for determinant
M1 for inverse
A1 for C.A - Reciprocal of
2.47 ×102
=0.4049 × 102=40.49
∛(3.025 ) =1.446
=40.49 ×1.446=58.55
M1 for reciprocal
M1 for ∛
A1 for C.A - 1 US dollar = Ksh 101.9378
20,000 = 20,000 ×101.9378
=Ksh 2038756
1 S.A = 7.6326
2038756 =2038756
7.6326
= 267111.6
= 267112 S.A
M1 for expression
M1 for expression
A1 for C.A - 5-3x ≤x-7 <11-2x
5x – 3x ≤x- 7 x-7 <11-2x
5+ 7 ≤x+3x x+2x <11+7
12 ≤4x 3x <18
3≤x x <6
3≤x <6
3,4 ,5
M1 for separating inequality
M1 for 3≤x and x <6
A1 for C.A - 5184 = 2×2×2×2×2×2×3×3×3×3
√5184=2×2×2×3×3
= 72
2744 = 2×2×2×7×7×7
∛2744=2×7=14
= 72/14 = 51/7
M1 for factors of 5184
M1 for factros of 2744
M1 for √ and ∛
A1 for C.A -
- A( 3,6) B(7,12) (x ,y)
Gradient of AB = 12-6 = 6 = 3
7-3 4 2
y - 6 = 3
x - 3 2
2(y – 6) = 3( x- 3)
2y – 12 = 3x – 9
2y = 3x – 9 + 12
2y = 3x + 3 - mid point of AB
3+7 , 6+12
2 2
(5,9) (x,y)
Perpendicular bisector gradient = - 2/3
(y-9 )/(x-5 )= -2/(3 )
3( y-9) = -2(x- 5)
3y – 2y = -2x + 10
3y = -2x + 10 + 27
3y = -2x + 37
AB ⊥BC gradient of Bc= - 2/3,B( 7,12)
(x,y ) x y-12 = -2/3 ) 3y= – 2x + 14 + 36
x-7
3y = -2x + 50
3(y-12)= -2(x-7)
3y – 36 = -2x + 14
M1 for gradient
M1 for expression
A1 for equation
M1 for mid point
M1 for gradient
M1 for expression
A1 for equation
M1 for expression= -2/3
M1 for x-multiplication
A1 for C.A
- A( 3,6) B(7,12) (x ,y)
-
- A ∶ B ∶ C
120000∶180000∶ 240000
12 ∶ 18 ∶ 24
2 ∶ 3 ∶ 4- 20/100 ×225000=45000
- 35/100 ×225000 = 78750
- Remainder = 225000-45000-78750
= 101 250
2: 3∶ 4 = 9
= 101250- 2/9 ×101 250 = 22,500
- 3/9 ×101 250 = 33,750
- 4/9 ×101 250 = 45,000
- 2:3:4=9
45000 - 4/9 ×45000 = 20,000
Chirchir new share = 240,000+20,000
= 260,000
M1 for multiplication
A1 for C.A
A1 for C.A
M1 for 101250
A1 for C.A
A1 for C.A
A1 for C.A
M1 for expression
M1 for addition
A1 for C.A
- A ∶ B ∶ C
-
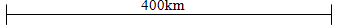
- Nairobi Mombasa
8.00am 8.30am
80Km/h 120Km/h
Time = D/S= 400̸/120̸ =31/3 hrs
= 3: 20min
+8∶ 30
3∶ 20
= 11 ∶ 50 am - Distance by coast bus for ½ hr.
= 80 × ½=40Km
R.D = 400 - 40 = 360 Km
R.S = 80 + 120 = 200Km/h
R.T = 260/200=14/5hr=1 hr:48min
Time met = 8∶ 30
1∶ 48
= 10: 18am - R.T = 14/5 hr
Coast by distance in 14/5
= 80 × 14/5
= 144 km
Distance = 40 + 144
= 184 - In 3hr20min coast bus covers
= 80 × 31/3
= 80 × 10/3 =266 2/3 km
Distance from Mombasa = 400 – 266 2/3
=1331/3 Km
M1 for 31/3 hr
M1 for addition
A1 for C.A
M1 for 40km
M1 for RD and R.S
M1 for expression of R.T
A1 for C.A
M1 for expression of distance
A1 for C.A
M1 for 400 – 266 2/3
A1 for C.A
- Nairobi Mombasa
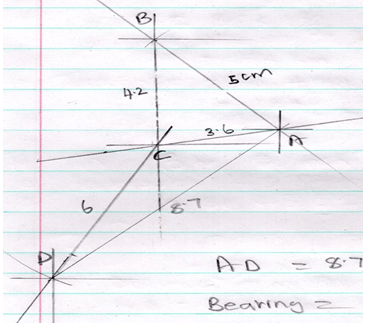
AD = 8.7 cm = 43.5 km ± 1
Bearing = 047º
B1 for point B
B1 for point C
B1 for Point D
B1 for 8.7 ± 0.1
A1 for 43.5 ± 1
A1 for 047º ± 1- y = x-6x+7
x 0 1 2 3 4 5 6 -x2 0 1 4 9 16 25 36 -6x 0 -6 -12 -18 -24 -30 -36 7 7 7 7 7 7 7 7 Y = x2 - 6x + 7 7 2 -1 -2 -1 2 7 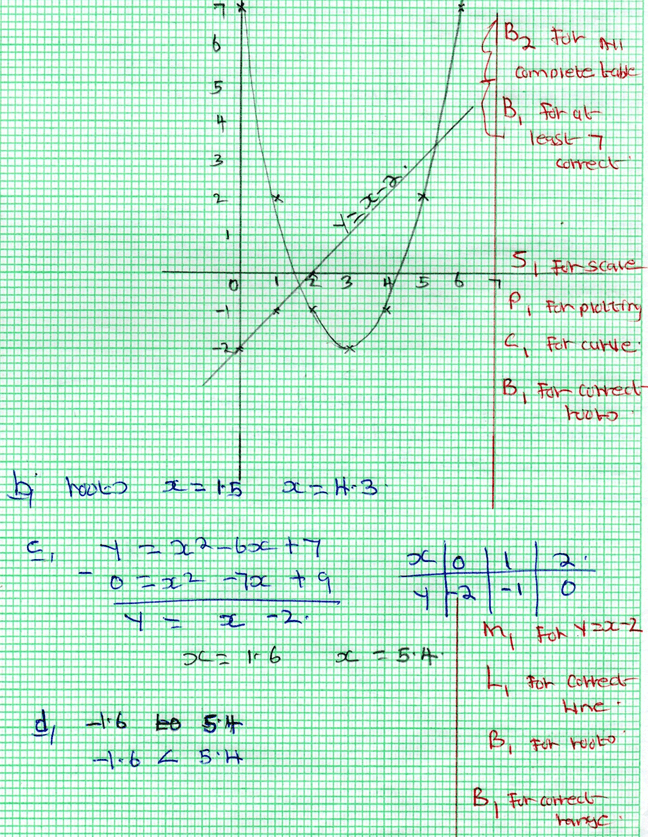
-
- <ROP= 128º
Angles on a straight line - <PSR= 116º
Angle on cyclic quadrilateral - <ORP= 26º
Base angle of isosceles triangle - <TRP= 64º
Angle between a chard a tangent( Nagle in alternate segment) - <RTP=53º
Angles on a triangle.
B1 for Angle
B1 for Reason
B1 for Angle
B1 for Reason
B1 for Angle
B1 for Reason
B1 for Angle
B1 for Reason
B1 for Angle
B1 for Reason
- <ROP= 128º
- AB height = ∛7.22- 3.42
= 6.347- Area ABC
= ½ 3.4 ×6.347
= 10.78
= 10.8 - Area of BCD = 10.8
A= ½ ×3.4 ×7.5 ×sinBCD
10.8
10.8 = 1.7 ×7.5 ×sinBCD=sinBCD
1.7 ×7.5
0.8471 sin BCD
sin-1 0.8471=BCD
= 57.8 = BCD - BD2=3.4+7.5-2×3.4 ×7.5 cos57.8
BD = 6.37 - <BDC = 34 3.4 = 6.37
sinBCD s inBDC sin57.8
Sin BDC – 3.4 × sin57.8
6.37
Sin BDC = 0.4517
BDC = sin-10.4517
BDC = 26.9
M1 for expression of height
M1 for expression of Area
A1 for C.A
M1 for expression of Area
M1 for 0.8471
A1 for C.A
M1 for expression
A1 for C.A
M1 for expression
A1 for C.A
- Area ABC
Marks x F Tx - A FT CF 48 – 52 50 3 -14 -42 3 53 – 57 55 4 -9 -36 7 58 – 62 60 10 -4 -40 17 63 – 67 65 12 1 12 29 68 – 72 70 8 6 48 37 73 – 77 75 3/40 11 33/-25 40 - Modal class 63 – 67
- Mean = A + ƸFt/ƸF
64 + -25/40
= 63 3/8
B1 for modal class
M1 for mid point
M1 for -25/40
A1 for C.A
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Kangundo Subcounty Pre Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

