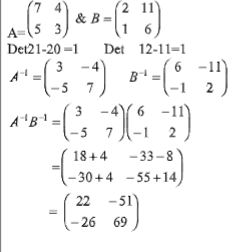Mathematics Paper 2 Questions and Answers - Kapsabet Pre Mock 2021/2022

MATHEMATICS
PAPER 2

INSTRUCTIONS TO CANDIDATES

• Write your name and Admission number in the spaces provided at the top of this page.
• This paper consists of two sections: Section I and Section II.
• Answer ALL questions from section I and ANY FIVE from section II
• All answers and workings must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
• Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

SECTION A

1. Use logarithms tables to evaluate (4mks)
   ³√36.72 x (0.46)²
       185.4
2. T is a transformation represented by the matrix  under T, a square of area 10cm² is mapped onto a square of area 110cm². Find the value of x (3mks)
3. Given that 2Cos(2x-30º)=-6/5 find x where 180º < x < 360º (3mks)
4. Make A the subject of the formula (3mks)
   T= 2m/n √^L-A/_3k
5. A quantity P is partly constant and partly varies inversely as square of t. P = 6 when t = 6 and p = 18 when t = 3. Find t when p = 11 (3mks)
6.              
   1. Expand (5 + ^x/₂)⁶ up to the term in x³. (2mks)
   2. Use your expansion to estimate the value of (¹¹/₆)⁶ . Correct to one decimal place. (2mks)
7. Solve for x in the equation. (3 Mks)
   Log₈ (x + 6) – Log8 (x – 3) = ²/₃
8. Solve for x and y in the simultaneous equation below. (3 mks)
   xy + 6 = 0
   x – 2y = 7
9. The size of each interior angle of a regular polygon is five times the size of the exterior angle. Find the number of sides of the polygon. (3mks)
10. If      1        -   2 + 2√5  = a + b√c find the value of a, b and c (3 mks)
        3- √5          3 + √5
11. The data below shows marks scored by 8 form four students in Molo district mathematics contest 44, 32, 67, 52, 28, 39, 46, 64.Calculate the mean absolute deviation. (3 Mks)
12. Steve deposited ksh.50, 000 in a financial institution in which interest is compounded quarterly. If at the end of second year he received a total amount of ksh79, 692.40. Calculate the rate of interest p.a (3 Mks)
13. The points with coordinates (5,5) and (-3,-1) are the ends of a diameter of a circle
    Centre A
    Determine:
    1. The coordinates of A (1mk)
    2. The equation of the circle, expressing it in form x2 + y2 + ax + by + c = 0 Where a, b, and c are constants (2mks)
14. Pipe x can fill an empty tank in 3 hours while pipe y can fill the same tank in 6 hours. When the tank is full, it can be emptied by pipe z in 8 hours. pipe x and y are opened at the same time when the tank is empty. If one hour later pipe z is also opened, find the total time taken to fill the tank. (3marks)
15. Fatima bought maize and beans from Kami. She mixed the maize and beans in the ratio 3: 2 she bought the maize at sh.90 per kg and the beans at sh.150 per kg. If she was to make a profit of 30% what would be the selling price of 1kg of the mixture. (3mks)
16. Given  and find A^‾1 B^-1 (3mks)

SECTION B

17.              
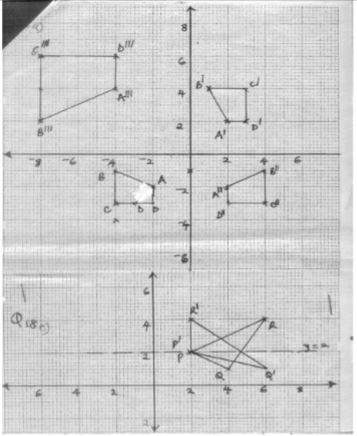
    1. A figure whose co-ordinates are A(-2, -2), B(-4, -1), C(-4, -3) and D (-2, -3) undergoes successive transformations ERS; where E, R and S are transformations represented by the matrices, On the grid provided, show the figure ABCD and its image under the successive transformations ERS. (6mks)
    2. Find the matrix representing the single transformation mapping the image found in (a) above back the object figure ABCD. (2mks)
       

       Marks	10-19	20-29	30-39	40-49	50-59	60-69	70-79	80-89	90-99
       Frequency	2	6	10	16	24	20	12	8	2

    3. Triangle PQR has vertices at P(2, 2), Q(4, 1) and R(6, 4). On the same grid, show the image of triangle PQR under a shear with line y = 2 invariant and point R(6, 4) is mapped onto R¹(2, 4). (2mks)
18. The following are marks by form four students in a mathematics test.
    Using an assumed mean of 54.5, calculate the
    1. Mean mark (4mks)
    2. Variance (4mks)
    3. Standard deviation (2mks)
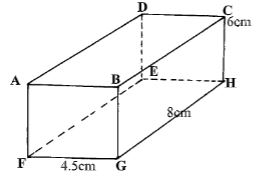
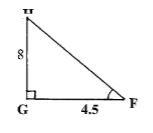
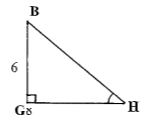
19. The diagram below represents a Cuboid ABCDEFGH in which FG =4.5cm, GH =8cm HC=6m
    
    
    1. Calculate the length FC (2mrks)
    2.          
       1. The size of the angle between the lines FC and FH (2mks)
       2. Size of the angle between the line AB and FH. (2mks)
    3. The size of the angle between the planes ABHE and the plane FGHE.(2mks)
    4. The total surface area of the cuboid (closed) (2mks)
20.              
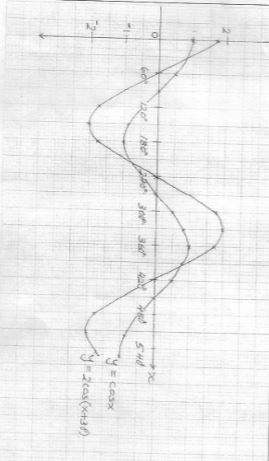
    1. Complete the table below, giving all your values correct to 2 d. p. for the functions y = cos x and y = 2cos (x + 30)º
       

       xº	0º	60º	120º	180º	240º	300º	360º	420º	480º	540º
       Cos x	1.00			-1.00		0.50
       2Cos(x+30)	1.73		-1.73		0.00

    2. For the function y = 2cos (x + 30)0
       State:
       1. The period (1mk)
       2. Phase angle (1mk)
    3. On the same axes draw the waves of the functionsy = cos x and y = 2cos (x + 30)º for 0º ≤ x ≤ 540.Use the scale 1cm rep 30º horizontally and 2cm rep 1 unit vertically. (4mks)
    4. Use your graph above to solve the inequality 2cos (x + 30o) ≤ cos x (2mks)
21. A teacher had 5 red, 6 black and 9 blue pens in a box. The pens were all identical except for the colour.
    1. If one pen is picked from the box, what is the probability that it is
       1. Red. (1mk)
       2. Not black. (1mk)
    2. The teacher asked a student to pick two pens from the box, one at a time, without replacement. Find the probability that
       1. Both pens are of the same colour. (3mks)
       2. They are of different colours. (2mks)
    3. If the first student was allowed to take away two blue pens and another student was asked to pick two pens without replacement. What is the probability that the second student picked pens of same colour? (3mks)
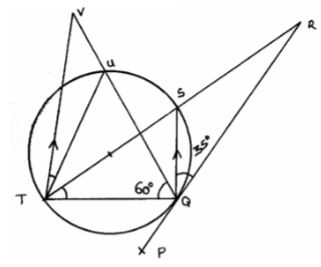
22. In the figure below, PQR is the tangent to the circle at Q. TS is a diameter and TSR and QUV are straight lines. QS is parallel to TV. Angle SQR = 35° and TQV = 60°.
    
    
    1. Find the following angles, giving reasons for each answer.
       1. QTS. (2mks)
       2. QRS. (2mks)
       3. QVT. (2mks)
       4. UTV. (2mks)
       5. QUT. (2mks)
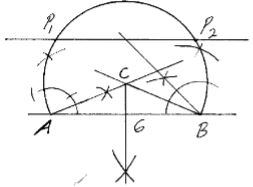
23. Use ruler and a pair of compasses only in this question
    1. Construct triangle ABC such that AB = 6cm, AC=BC and angle ACB = 135° 4mks
    2. On one side only construct the locus of P such that:
       1. < APB = 67.5° 1mk
       2. area of triangle , APB = 9cm² 3mks
    3.         
       1. Locate P1 and P2 the two possible positions of P which satisfy the two conditions above 1mk
       2. Measure the distance between P1 and P2. 1mk
24. An arithmetic progression has the first term a and the common difference d.
    1. Write down the third, ninth and twenty – fifth terms of the progression. (3 Mks)
    2. The progression is increasing and the third, ninth and twenty-fifth terms form the first three Consecutive terms of a geometric progression. If the sum of the seventh term and twice the sixth term of the arithmetic progression is 78.
       Calculate
       1. The first term and the common difference (5 Mks)
       2. The sum of the first nine terms of the arithmetic progression (2 Mks)

MARKING SCHEME

1.        
   

   No	Log
   36.72             (0.46)2 ⇒ 2 (‾1.6628) 3.474 x 10-1 =0.3474

2. A.S.F = det
   5x2 + 6 = 110/10
   5x2 + 6 -11 = 0
   5x2 = 5
   x = ± 1
   
   
3. 2 cos(2x – 30) = -6/5
   Cos(2x -30) = - 0.6
   Cos –ve in 3rd quad
   2x – 30 = 53.13
   2x – 30 = 233.13
   2x = 263.10
   x = 131.57°
   2x-30=540-53.13
   X=258.44
   2x - 30°= 360 + 233.13°
   2x = 623.13
   x = 311.57
   x=131.57,258.44,311.57
   
   
4. ^nT/_2m = √ ^L-A/_3k  
   
     n²T²   =    L - A  
     4m²           3K
   4m² (L – A) = 3k (n² T²)
   4Lm² – 4Am² = 3kn²T²
   A =   4LM²   - 3kn²T²
               4m²
   
   
5. p=c + ^k/_t²
   6= c + ^k/₃₆
   18=c + ^k/₉
   216 = 36c + k ----- (i)
   162 = 9 c + k --------(ii)
     54 = 27c
   ⁵⁴/₂₇ = c = 2 k = 144
   when p = 11
   11 = 2 + ¹⁴⁴/_t²
   9t² = 144
   t = 4
6.            
   1. Coefficients: 1     6      15     20
      Terms: 5⁶, 5⁵ (^x/₂), 5⁴(^x/₂)², 5³ (^x/₂)³
      15625, ^3125x/₂, ^625x²/₄, ^125x³/₈
      ( 5 + x/2)⁶ = 15625 + ³¹²⁵/_3x + ^9375x³/₄ + ^625x³/₂ + ...
      x= 1 Therefore, (11/2)⁶ =  15625 + ³¹²⁵/₃ + ⁹³⁷⁵/₄ + ⁶²⁵/₂
   2. = 15625 + 1041.667 + 2343.75 + 312.5
      =19322.9
7. Log8 (^x+6/_x-3) = Log₈8^{²/₃
   x+6}/_x-3 = 4
   x + 6 = 4x – 12
   3x = 18
   x = 6
   
   
8. 8 x = 7 + 2y
   ( 7 + 2y) y + 6 = 0
   7y + 2y² + 6= 0
   2y² + 7y + 6 = 0
   2y² + 4y + 3y + 60 = 0
   2y(y + 2) +3 (y + 2) = 0
   (2y + 3) ( y + 2) = 0
   When y =-2, x = 3
   y =^-3/₂₁, x = 4
   
   
9. X+5X=180
   6X=180
   X=30
   360/30
   12 sides 
10.   1( 3 + √5) - ( 2 + 2√5)(3- √5)
                 (3 - √5)(3 + √5)
    3 + √5 - [6-2√5 + 6√5 -10]
                 9-5
    3+√5 - 4√5 + 4
             4
    7 - 3√5 =    7   - 3 √5
         4           4       4
    hence a = ⁷/₄, b= ^-3/₄ and c =5
    
    
11. Mean = 44 + 32 + 67 + 52 +28 + 39 + 46 + 64
    372/8 = 46.5
    

    x	44	32	67	52	28	39	46	64
    d	-2.5	-14.5	20.5	5.5	-18.5	-7.5	-0.5	17.5
    (d)	2.5	14.5	20.5	5.5	18.5	7.5	0.5	17.5

    Mean absolute deviation
    Σxd =  87   = 10.875
      N       8
12. ^50,000/_50,000 ( 1 + r/100)⁸ =  ^79692.40/_50,000
    ⁸√(1 + r/1000) = ⁸√1.593848
    1 + ^r/₁₀₀ = 1.06
    ^r/₁₀₀ = 0.06
    R = 6% per interest period
    Per annum = 6 x 4 = 24%
    
    
13.            
    1. Co – ordinate of
       A ( ^5-3/₂  ^5-1/₂)
       A (²/₂   ⁴_/2)
       A ( 1,2)
       
       
    2. r = √(5-1)² + (5-2)²
       =√16+9
       =5 units
       ( x – 1)² + ( y – 2) ² = 5²
       x² – 2x+ 1 + y²- 4y + 4 = 25
       x² + y² – 2x - 4y + 5 = 25
       x² y² – 2x – 4y – 20 = 0
       
       
14. x fills ¹/₃ of tank in 1 hour
    y fills ¹/₆ of tank in 1 hour
    z empties ¹/₈ of tank in 1 hour
    x and y open will fill ¹/₃ + ¹/₆ = ¹/₂ of tank in 1 hour
    remaining fraction = 1 - ¹/₂ = ¹/₂
    x, y and z both will fill ¹/₃ + ¹/₆ - ¹/₈ = ³/₈ of tank in 1 hour
    time taken by x, y and z to fill ½ of remaining tank
    = ¹/₂ ÷ ³/₈=1 ¹/₃ hours
    Total time = 1 + 1 ¹/₃ = 2 ¹/₃ hours
15. M:B
    3:2
    3 x 90 x 150 x 2 = cost price
         3+ 5
    CP= 270 + 300
                  8
    S.P = ¹³⁰/₁₀₀ + 71.25
    = Ksh 92.625
    =Ksh 92.60
16.    
    
    Det21-20 =1 Det 12-11=1
    
17.        
    1.     
       
    2. S1 R1 E1 (A”’B ”’C ”’D ”’) = ABCD
       
    3. ΔPQR – For object figure plotted correctly
       PQR – For image figure plotted correctly
       
18.          
    

    marks	f	Mp(x)	d(x-A)	fd	d2	fd2
    10-19 20-29 30-39 40-49 50-59 60-69 70-79 80-89 90-99	2 6 10 16 24 20 12 8 2	14.5 24.5 34.5 44.5 54.5 64.5 74.5 84.5 94.5	-40 -30 -20 -10 0 10 20 30 40	-80 -180 -200 -160 0 200 240 240 80	1600 900 400 100 0 100 400 900 1600	3200 5400 4000 1600 0 2000 4800 7200 3200
    				140		31400

    
    
    1. Mean = A + ^∑fd/_∑f
       = 54.5 + ¹⁴⁰/₁₀₀ = 55.9
       
       
    2. Variance = ³¹⁴⁰⁰/₁₀₀ – (¹⁴⁰/₁₀₀)²
       = 312.04
    3. standard deviation = √variance
       = √312.04 = 17.66
19.             
    1. FC = √6² + 4.5² + 8²
       = 10.97
    2.        
       1. Sin θ = 6
          0.97
          θ = 33.16
          
          
       2.    
          
          Tan θ = 8 ÷ 4.5
          = 1.778
          θ = 60.64
    3.    
       
       Tan θ = 6 ÷8
       θ = 36. 87
       
       
    4. Total surface area
       2 (8 x 6) + 2 (4.5 x 8) + 2(4.5 x 6)
       = 222cm²
20.      
    1.    
       

       xº	0º	60º	120º	180º	240º	300º	360º	420º	480º	540º
       Cos x	1.00	0.50	-0.50	-1.00	-0.5	0.50	1.00	0.50	-0.50	-1.00
       2Cos(x+30)	1.73	0.00	-1.73	-1.73	0.00	1.73	1.73	0.00	-1.73	-1.73

    2.        
       1. Period = 360º
       2. phase angle = 30º
    3.     
       
       
       
    4. 37.5º ≤ x ≤ 217.5º
       397.5º ≤ x ≤ 540º
21.          
    1.         
       1.  ⁵/₂₀ = ¹/₄
          
       2.   ⁵/₂₀ + ⁹/₂₀
          =¹⁴/₂₀ = ⁷/₁₀
    2.               
       1.   ( ⁵/₂₀ X ⁴/₁₉)+(⁶/₂₀ X ⁵/₁₉₎ + (⁹/₂₀ X ⁸/₁₉)
          = 20/380 + 30/380 + 72/380
          = ¹²²/₃₈₀ = ⁶¹/_{190
          =} 1- ⁶¹_{/90
          =} ²⁹/₉₀
22.                    
    1. <QTS = <SQR = 35° B1
       Angles in alternate segments 
       
       
    2. <QST = 55° B1  
       <QRS = 55 - 35° B1  
         = 20°
       
       
    3. <QVT = <SQV = 30°
    4. 90 – (30° + 35)  = 25°
    5. 180 – (60° + 65°) = 55°
       
       
23. ½ x 6x h = 9✓
    h= 3✓
    P₁p₂ = 5.6 cm
    
24.          
    1. T₃ = a + 2d
       T₉ = a + 8d
       T₂₅ = a + 24d
       
       
    2.      
       1. ^a+8d/_{a+2d =} ^a+24d/_a+8d
          a² + 2bad + 48d² = a² + 16ad + 64d²
          10ad = 16d²
          a = ^16d/₁₀ or ⁸/_5d
          a + 6d + 2(a + 5d) = 78
          3a + 16d = 78
          24d + 80d = 390
          104d = 390
          d = 3.75
          a = ⁸/₅ x 3.75
          a = 6
          
          
       2. S₉ = 4.5 (12 + (8 X 3.75)
          4.5 (12 + 30)
          = 4.5 (42)
          = 189
          (10 Marks)