MATHEMATICS
PAPER 1
SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.
- Evaluate (3 marks)
¹/₃ of 2¹/₃ + ²/₃(1²/₃-1¹/₂)
³/₄ of 3¹/₃÷¹/₄ - Solve the inequality below. Hence state the integral values. (3 marks)
x < 2x+7 ≤ -1/3x+14 - The sum of interior angles of a triangle is given by (10x-2y)º while that of a hexagon is given by (30x-24y)º. Calculate the values of x and y. (3 marks)
- The equation of the line is given by 3y=2x+15. Given that the L1 cuts the x axis at a point A.
- Find the coordinates of A (2 marks)
- Find the angle the line L1 makes with the x axis. (2 marks)
- In the triangle below, BE is parallel to CD. BE=10cm, CD=15cm and the area of the trapezium BCDE is 75cm2, calculate the area of triangle ACD. (3 marks)
- A and B are on the same side of the tower. The angles of elevation of the top of the towers from A and B are 320 and 500 respectively. If AB = 15cm. calculate the height of the tower to 2 decimal places. (4 marks)
- Solve the equation 4x+1 1/8(2x-3) =√2 (3 marks)
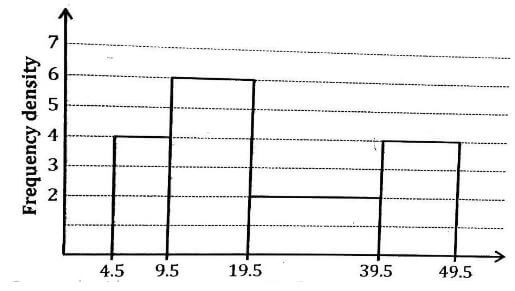
- The diagram below shows a histogram from marks obtained in a certain test.
Use the histogram to make the frequency table for the distribution. (3 marks) - A sales lady earns a basic salary of sh. 12400 per month. In addition, she gets a commission of 2% on the first sh. 80000 worth of goods and a commission of 3% on goods worth above sh. 80000. In a certain month, she earned a total of sh. 20000. Calculate the value of goods sold that month. (3 marks)
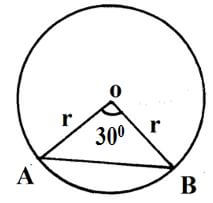
- The figure below shows a circle centre O. Chord AB subtends 300 at the centre. If the area of the minor segment is 5.25cm2, find the radius of the circle. (3marks)
- Simplify the following expression completely. (3 marks)
12a² - 3b²
2a² - ab - b² - A commercial bank in Kenya buys and sells foreign currency as shown in the table below.
James who is going for studies in USA had Ksh. 1,236,600.Buying (Ksh) Selling(Ksh) 1 US $ 100.36 100.92 1 Sterling pound 130.52 130.64 - Calculate the amount of money in dollars he had to the nearest dollar. (1 mark)
- His father who works in England sent him 4000 sterling pounds, while he was still in Kenya. Find the total amount in dollars he left with to USA. (2 marks)
- Wekesa and Ndida working together can cultivate a piece of land in 6 days. Wekesa alone can complete the work in 15 days. After the two had worked for 4 days Wekesa withdrew the services. Find the time taken by Ndinda to complete the remaining work. (3 marks)
- Given that sin θ=3/5 and 90º ≤ θ ≤ 180º, find without using trigonometric tables, the value of 2tanθ+3cosθ (3 marks)
- Use square, square root and reciprocal tables only to evaluate the following giving your answer to 2 decimal places. (3 marks)
2 + 2
√34.46 (8.67)² - The sum of digits formed in a two digit number is 16. When the number is subtracted from the number formed by reversing the digits, the difference is 18. Find the number (3 Marks)
SECTION II(50 Marks)
Answer any five questions in this section in the spaces provided.
- A group of choir members decided to raise ksh. 3600 to buy a guitar. Each member was to contribute equal amount. In the preparation process five members transferred to another church, that meant the remaining contributors had to pay more to achieve the target.
- Show that the increase in the contribution per member was:
18000/n(n-5) if n is the initial number of members. (4 marks) - If the increase in the contribution per member was Ksh. 24, what was the original contribution before the other members left? (4 marks)
- Calculate the percentage increase in the contribution before the others left. (2 marks)
- Show that the increase in the contribution per member was:
-
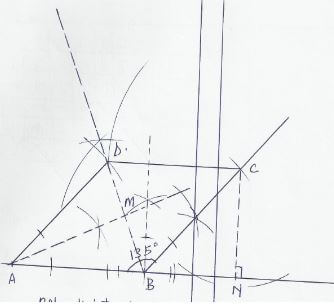
- Using a ruler and a pair of compasses only construct a rhombus A B C D such that AB = 6cm and <ABC = 135º. (4 marks)
- Drop a perpendicular from C to AB extended to meet AB at N. Measure BN and CN. (2 marks)
- Bisect <ABC and <DAB, let the two bisectors meet at M. Measure MA. (2 marks)
- Determine the area of triangle ABM. (2 marks)
- A village Q is 7 km from village P on a bearing of 045º. Village R is 5 km from village Q on a bearing of 120º and village S is 4 km from village R on a bearing of 270º.
- Taking a scale of 1cm to represent 1 km, locate the four villages. (4 marks)
- Use the scale drawing to find the:
- Distance and bearing of the village R from village P. (2 marks)
- Distance and bearing of village P from village S. (2 marks)
- Area of the polygon PQRS to the nearest 4 significant figures. (2 marks)
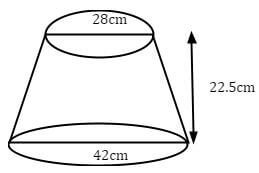
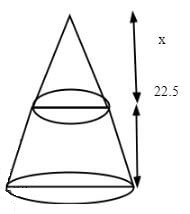
- The diagram below represents a solid frustum with base diameter 42cm and top diameter 28cm. the frustum is 22.5cm high and is made of a metal whose density is 3 g/cm3 (take π=22/7)
- Calculate the volume of the metal in the frustum. (5 marks)
- Calculate the mass of the frustum in kg. (2 marks)
- The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube. (3 marks)
- A solution whose volume is 80 litres is made up of 40% of water and 60% of alcohol. When x litres of water is added the percentage of alcohol drops to 40%.
- Find the value of x. (4 marks)
- Thirty litres of water is added to the new solution. Calculate the percentage of alcohol in the resulting solution. (2 marks)
- If 5 litres of the solution in (b) above is added to 2 litres of the original solution. Calculate in the simplest form, the ratio of water to that of alcohol in the resulting solution. (4 marks)
- A truck left town X at 11.45am and travelled towards town Y at an average speed of 60 km/hr. A car left town x at 2.15pm on the same day and travelled along the same road at an average speed of 100km/hr. The distance between the two towns is 500km.
- Calculate the time of the day when the car overtook the truck. (4 marks)
- The distance from Y when the car overtook the truck. (3 marks)
- After overtaking the bus, both vehicles continued towards Y at their original speeds. Find how long the car had to wait at town Y before the ruck arrived. (3 marks)
-
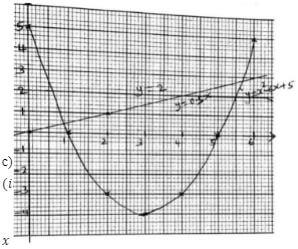
- Complete the table below for the equation y=x2-6x+5. (2 marks)
x 0 1 2 3 4 5 6 x² 0 4 9 25 -6x 0 -6 -24 -36 5 5 5 5 5 5 5 5 y 5 0 - Draw the graph of y=x² - 6x + 5 using the values in the table. (3 marks)
- use the graph to solve the equations.
- x² - 6x + 5 = 0 (1 mark)
- x² - 6x + 7 = 0 (2 marks)
- x² - 6.5x + 5 = 0 (2 marks)
- Complete the table below for the equation y=x2-6x+5. (2 marks)
- A business lady bought 100 quails and 80 rabbits for Sh. 25,600. If she had bought twice as many rabbits and half as many quails she would have paid Sh. 7,400 less. She sold each quail at a profit of 10% and each rabbit at a profit of 20%.
- Form two equations to show how much she bought the quails and the rabbits (2 Marks)
- Find the cost of each (3 Marks)
- Calculate the profit she made from the sale of the 100 quails and 80 rabbits (3 Marks)
- What percentage profit did she make from the sale of the 100 quails and 80 rabbits (2 Marks)
MARKING SCHEME
- ¹/₃ of ⁷/₃ + ²/₃(⁵/₃-³/₂)
(³/₄ of ¹⁰/₃÷¹/₄)
⁷/₉ + ²/₃ (¹/₆)
(⁵/₂×⁴/₁)
⁷/₉+¹/₉
10
(⁸/₉)/₁₀= ⁴/₄₅ - x ≥ -7
x < 3
-6,-5,-4,-3,-2,-1,0,1,2 - 10x-2y=180
30x-24y=720
30x-24y=720
30x-6y=540
-18y=180
y=10,x=16 -
- When y=0
0=2x+15, x = -7.5
A(-7.5,0)
y=2/3 x+5 - Tan θ=2/3,
θ=33.69
- When y=0
- L.S.F=10:15=2:3
A.S.F=4:9
Area of small triangle: Area of big triangle=x:x+75
4/9=x/(x+75)
9x=300+4x
5x=300
x=5 - h=xtan50º
h=(x+15)tan30º
xtan50º=(x+15)tan32º
x=15tan32º/tan50º-tan32º =16.53
h=16.53 × tan50º=19.70m - 22(x+1) × 2-3(2x-3) = 21/2
2x+2-6x+9=1/2
-4x=-10 1/2
x=2.625 - Frequency table
class 5-9 10-19 20-39 40-49 frequency 20 60 40 40 - 2/100 × 80000=1600
3/100 × x=20000-(12400+1600)
x=200000
total sales=280000 - 30/360 X 22/7 x r2 - 1/2r2 Sin 30º = 5.25
1/42r2 - 1/4r2 = 5.25
1/84r2 = 441
r= ± 21cm
r=21cm - 3(2a+b)(2a-b)
(2a+b)(a-b)
= 3(2a-b)
a-b -
- 1,236,000/100.92=12,247
- 4000×130.52=522,080
522,080/100.92=5173
Total amount in dollars=12247+5173
=17420
- Wekesa + Ndinda = 6 days
1 day work by both = 1/6 of work
4 days work by both = 4/6 of work
remaining work=2/6 = 1/3 of work
wekesa alone = 15 days
1 day work alone =1/15 days
wekesa alone 4 days =4/15
∴work for Ndinda alone in 4 days
=4/6 - 4/15 = 3/30 = 1/10
time to finish work remaining
Ndinda=1/3×10=3 1/3 days - tanθ=-3/4
cosθ=-4/5
2(-3/4) + 3(-4/5)
-6/4 - 12/5=-78/20
= - 39/10 - 2(1/√34.46)+2(1/8.672)
2(1/5.8703)+2(1/75.17)
2(0.1704)+2(0.0133)
0.3408+0.0266=0.3574 - Let the digits be x and y
x + y = 16 ………..(i)
original no.= 10x + y
reversed no.= 10y + x
(10y + x)– (10x + y)= 18……..ii
x + y = 16
9y – 9x = 18
9y + 9x = 144
9y – 9x = 18
18x = 126
x = 7
y = 9
The no.is 79 -
- Original contribution =3600/n
new contribution=3600/(n-5)
Increase=3600/(n-5) - 3600/n
3600n-3600n+18000
n(n-5)
=18000/n(n-5) - 18000/n(n-5) =24
18000=24n2-120n
n2 - 5n - 750=0
n2 - 30n + 25n - 750=0
n(n-30)+25(n-30)=0
n-30=0
n+25=0
But n cannot be -ve∴n=30 - 3600/n=120 (original)
3600/25=144 (new)
Increase =24/120×100%=20%
- Original contribution =3600/n
-
BN = 4.1 + 0.1
CN = 4.3 + 0.1
MA = 5.5cm
Area = ½ × 2.7 × 24
= 6.48cm2 -
-
-
- 9.6km±0.1
75º±1 - 5.8km±0.1
246º±1 - Area=1/2 × 7 × 5sin105º -1/2 × 4 × 5.8sin154
=16.9037 - 5.0851
=11.8186
- 9.6km±0.1
-
-
- 42/28=22.5+x/x
42x=630+28x
14x=630
∴x=45
volume of whole cone=
=1/3 × 22/7 × 21 × 21 × 67.5 = 31185cm3
volume of small cone=
=1/3 × 22/7 × 14 × 14 × 45 - 9240cm3
volume of frustum= 31185 - 9240= 21945cm3 - Mass of the frustum=21945×3=65835g
mass in kg = 65835/1000 = 65.835kg - 20% of 65.835kg=13.167kg
65.835-13.167=52.668kg
Volume of the remaining material=
52668g/3=17556 cm3
length of the cube = ∛17556=25.99cm
- 42/28=22.5+x/x
-
- vol of water=40/100 × 80=32litres
vol of alcohol= 60/100 × 80=48litres
48/(80+x) × 80=40
4800=40(80+x)
x=40 - Total value = 80+40+30=150litres
48/150 × 100=32% - Vol of alcohol=32/100 × 5 + 60/100 ×2
=1.6+1.2=2.8litres
vol of water
=5 - (32/100 × 5) + 2 -(60/100 × 2)
3.4+0.8=4.2litres
Water:alcohol=4.2:2.8=3:2
- vol of water=40/100 × 80=32litres
-
- Truck has covered at 2:15pm=60 × 2 1/2
=150km
relative speed=100 - 60=40km/hr
T = 150/40=3.75hours
=3hours45minutes
=1415+0345
=1800hrs/6:00pm - distance from y
=3.75×100=375km
= 500-375=125km - 125/60 - 125/100
=2 1/12 hrs - 1 1/4 hrs
=5/6 × 60
=50minutes
- Truck has covered at 2:15pm=60 × 2 1/2
-
-
x 0 1 2 3 4 5 6 x² 0 1 4 9 16 25 36 -6x 0 -6 -12 -18 -24 -30 -36 5 5 5 5 5 5 5 5 y 5 0 -3 -4 -3 0 5 -
-
- x=1,x=5
- y=x2 - 6x+5
0=x2 - 6x+7
y=-2
x=0.6,x=5.5 - y=x2 - 6x+7
0=x2 - 6.5x + 7
y=0.5x
x=0.8,x=5.7
- x=1,x=5
-
-
- 100q + 80r = 25600
50q + 160r = 18200 - 200q + 160r = 51200
50q + 160r = 18200
150q = 33000
q = 220
r = 45 - 110/100 × 220 = 242
120/100 × 45 = 54
100(242) + 80 (54) = 28,520
Profit = 28520 – 25600 = 2920 - Percentage profit=2920/25600×100
= 11.41%
- 100q + 80r = 25600
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - MECS Cluster Joint Pre Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students