PHYSICS
PAPER ONE
SECTION A: (25 MARKS)
Answer all the questions in this section.
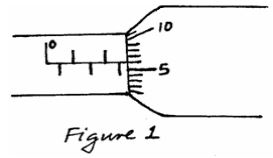
- A micrometer screw gauge is used to measure the thickness of a stuck of 10 microscope slide cover slips. The reading with the cover slips in position is as shown in figure 1.
If the micrometer screw gauge has a zero error of -0.01mm, determine the thickness of each cover slip. (2 marks) - Smoke particles observed through a microscope are seen to move randomly. Explain this observation (2marks)
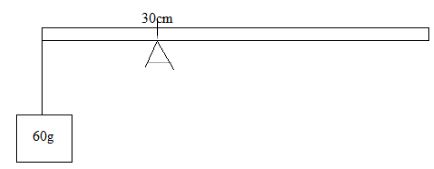
- Figure 4 below shows a uniform metre rule balanced by a mass of 60g suspended at 0 cm mark. If the pivot is at 30 cm mark, Calculate the weight of the metre rule (3marks)
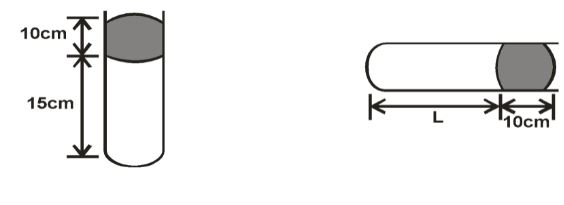
- A column of air 15cm is trapped by mercury thread of 10cm as shown below. Calculate the length of the trapped air when the tube is laid horizontally given that atmospheric pressure is 76cmHg. (3 Marks)
- A water pipe of diameter 5.2cm is connected to another pipe of diameter 1.3cm. The speed of water in the smaller pipe is 3ms-1 . Calculate the speed of water in the larger pipe. (2 Marks)
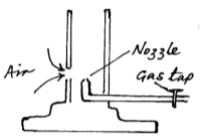
- The figure below shows a Bunsen burner.
Use the Bernoulli’s Principle to explain how air is drawn into the burner when the gas tap opened. (2 marks) - χ m³ of a substance which has a density of 0.8/gcm³ is mixed with 1000cm³ of sea water of density 1020kg/m³. The density of the mixture is 960kg/m³. Determine the value of χ. (3 marks)
- State one factor that affects spring constant. (1 mark)
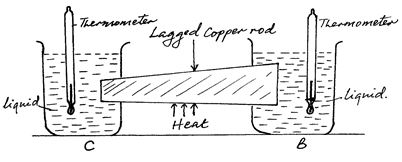
- Figure below shows samples of the same liquid B and C being heated through a well-lagged copper rod of non-uniform cross-sectional area. A thermometer is placed in each sample for some time.
If the rod is being heated at the middle, state and explain which of the thermometers records a higher temperature. (2 marks) - An object weighs 1.04 N in air, 0.64N when fully immersed in water and 0.72N when fully immersed in a liquid. If the density of water is 1000kg/m3, find the density of the liquid. (3 marks)
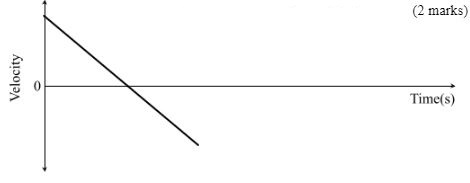
- A stone is thrown vertically upwards from an edge of a platform. Eventually the stone lands without bouncing, on the ground below the platform. Taking the upward velocity to be positive, sketch, on the axes provided the velocity-time graph of the motion of the stone. (2 marks)
SECTION B 55 MARKS
Answer all questions in this section in the space provided
-
- A boy throws a tennis ball vertically upwards from a truck moving at a constant velocity. Give the reason why the ball lands back exactly the same point where it was projected from. (1 mark)
- A trailer of mass 30 tonnes travelling at a velocity of 72km/hr rams onto a stationary bus of mass 10 tonnes. The impact takes 0.5 seconds before the two vehicles move off together at a constant velocity for 15 seconds. Determine.
- The common velocity. (3 marks)
- The distance moved after the impact. (1 mark)
- The impulsive force on the trailer on impact. (2 marks)
- Give the reasons why a safety seat belt used in a vehicle should have a wide surface area. (1 mark)
-
- The tape in the figure below was obtained from an experiment using a ticker timer of frequency 50Hz. The tape was pulled by a trolley.
If the trolley that was pulling the tape was accelerating,- Show on the diagram, the direction of acceleration of the trolley. (1 Mark)
- Calculate the acceleration of the trolley. (4 Marks)
- A stone is allowed to fall freely from the top of a tower 60 metres high. At the same time, a second stone is thrown vertically upwards with a velocity of 20m/s from the ground. Find;
- The time taken by the two stones before they meet. (3 Marks)
- The height at which the two stones meet from the point of projection. (2 Marks)
- The tape in the figure below was obtained from an experiment using a ticker timer of frequency 50Hz. The tape was pulled by a trolley.
-
-
- State Archimedes’ Principle. (1mark)
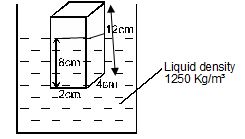
- Figure below shows a block of dimensions 2cm × 4cm × 12cm floating in a liquid of density 1250kg/m³ whose submerged depth is 8 cm.
Find- The upthrust on the block. (3 marks)
- The weight of the block. (1 mark)
- Given that gravitational pull is 10 N/Kg, calculate density of the block. (3 marks)
-
-
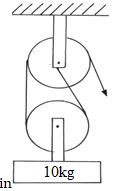
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N.
- How much potential energy does the load gain. (2 marks)
- How far does the effort end move in order to raise the load by 2m? (1 mark)
- How much work is done by the effort (2 marks)
- What is the efficiency of these pulleys? (2 marks)
- If all the wasted energy is used to lift the bottom pulley, how much does the pulley weigh? (2 marks)
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N.
-
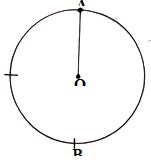
- A stone of mass 450g is rotated in a vertical circle at 3 revolutions per second. If the string has a length of 1.5m, determine:
- The linear velocity. (2mks)
- The tension of the string at position A (2 marks)
- The tension of the string at position B (2 marks)
- A stone is whirled with uniform speed in horizontal circle having radius of 10cm. it takes the stone 10 seconds to describe an arc of length 4cm.
- The angular velocity ω. (2 marks)
- The period time T. (2 marks)
- State one factor affecting centripetal force. (1 mark)
- A stone of mass 450g is rotated in a vertical circle at 3 revolutions per second. If the string has a length of 1.5m, determine:
-
- State what is meant by the term specific latent heat of vaporization? (1 mark)
- In an experiment to determine the specific latent heat of vaporization of water, steam at 100ºC was passed into water contained in a well lagged copper calorimeter. The following measurements were made.
Mass of calorimeter =40g
Initial mass of water =80g
Final mass of calorimeter + water + condensed steam = 123g
Initial temperature of water + calorimeter = 5º C
Final temperature of mixture = 30ºC
(specific heat capacity of water=4200JKg-1K-1 and specific heat capacity of copper=390 JKg-1K-1.}
Determine:- Mass of the condensed steam. (1 mark)
- Heat gained by calorimeter alone (2 marks)
- Heat gained by water only. (2 marks)
- Given that L is the specific latent heat of vaporization of steam
- Write an expression for the heat given out by steam. (1 mark)
- Determine the value of L (3 marks)
MARKING SCHEME
- A micrometer screw gauge is used to measure the thickness of a stuck of 10 microscope slide cover slips. The reading with the cover slips in position is as shown in figure 1.
If the micrometer screw gauge has a negative zero error of 0.01mm, determine the thickness of each cover slip. (2 marks)- 2.5+0.06= 2.56① + 0.01= 2.5
2.57÷10=0.257mm✓①
- 2.5+0.06= 2.56① + 0.01= 2.5
- Smoke particles observed through a microscope to move random. Explain this observation (2marks)
- Due to uneven bombardment ✓①of smoke particles by invisible air molecules. ✓①
- Due to uneven bombardment ✓①of smoke particles by invisible air molecules. ✓①
- Figure 4 below shows a uniform metre rule balanced by a mass of 60g suspended at 0 cm mark. If the pivot is at 30 cm mark, Calculate the weight of the metre rule (3marks)
- Clockwise movement = Anti clockwise movement
W X 20 =0.6 X 30
W=0.6 X 30
20
W=0.9 N
- Clockwise movement = Anti clockwise movement
- A column of air 15cm is trapped by mercury thread of 10cm as shown below. Calculate the length of the trapped air when the tube is laid horizontally given that atmospheric pressure is 76cmHg. (3 marks)
- P₁V₁ = P₂V₂✓①
(76 + 10)15 = 76 x L✓①
L = (86 ×15)/76
= 16.97 cm✓①
- P₁V₁ = P₂V₂✓①
- A water pipe of diameter 5.2cm is connected to another pipe of diameter 1.3cm. The speed of water in the smaller pipe is 3ms-1. Calculate the speed of water in the larger pipe. (2 Marks)
- ALVL = ASVS
π x 2.6 x 2.6 x VL = π x 0.65 x 0.65 x 3 √1
= 0.1875 m/s √1
- ALVL = ASVS
- The figure below shows a Bunsen burner.
Use the Bernoulli’s Principle to explain how air is drawn into the burner when the gas tap opened. (2 marks)- When the gas tap is opened the gas at the nozzle moves with a very high velocity hence reduced pressure, pressure outside become greater than pressure around the nozzle forcing air in which mixes with the gas to be ignited up.
- When the gas tap is opened the gas at the nozzle moves with a very high velocity hence reduced pressure, pressure outside become greater than pressure around the nozzle forcing air in which mixes with the gas to be ignited up.
- χm³ of a substance which has a density of 0.8/gcm³ is mixed with 1000cm³ of sea water of density 1020kg/m³. The density of the mixture is 960kg/m³. Determine the value ofχ. (3 marks)
- Mass= density × volume density of mixture = (800x + 1.02 )/(x + 0.001)=960✓①
= 800× x ✓①
=1020× 0.001 800x + 1.02 =960x +0.96
0.06 = 160x
X =3.75×10-4 kg/m3 ✓①
- Mass= density × volume density of mixture = (800x + 1.02 )/(x + 0.001)=960✓①
- State one factor that affects spring constant. (1 mark)
- Thickness of the spring✓①
- Material of the spring✓①
- Figure below shows samples of the same liquid B and C being heated through a well-lagged copper rod of non-uniform cross-sectional area. A thermometer is placed in each sample for some time.
If the rod is being heated at the middle, state and explain which of the thermometers records a higher temperature. (2 marks)- Thermometer B✓①- temperature increases with an increase in cross sectional area✓①
- Thermometer B✓①- temperature increases with an increase in cross sectional area✓①
- An object weighs 1.04 N in air, 0.64N when fully immersed in water and 0.72N when fully immersed in a liquid. If the density of water is 1000kg/m3, find the density of the liquid. (3 marks)
- Up thrust in liquid =1.04-0.72=0.32N✓①
- Up thrust in water=1.04-0.64=0.40N✓①
- Density of liquid=100Kg/m3× 0.32/0.40 = 0.8×103Kg/m3✓①
- A stone is thrown vertically upwards from an edge of a platform. Eventually the stone lands without bouncing, on the ground below the platform. Taking the upward velocity to be positive, sketch, on the axes provided the velocity-time graph of the motion of the stone. (2 marks)
-
- A boy throws a tennis ball vertically upwards from a truck moving at a constant velocity. Give the reason why the ball lands back exactly the same point where it was projected.
- The ball has the same horizontal velocity as the truck ✓① (1 mark)
- A trailer of mass 30 tonnes travelling at a velocity of 72km/hr rams onto a stationary bus of mass 10 tonnes. The impact takes 0.5 seconds before the two vehicles move off together at a constant velocity for 15 seconds. Determine.
- The common velocity. (3 marks)
- M₁U₁+ M₂U₂ = V(M₁ + M₂)✓①
30,000 x 20 + 0 = V (30,000 + 10,000)
V= 600,000/40,000✓①
= 15msˉ¹ ✓①
- M₁U₁+ M₂U₂ = V(M₁ + M₂)✓①
- The distance moved after the impact. (1 mark)
- S = Vt
= 15 x 15 ✓①
= 225m ✓①
- S = Vt
- the impulsive force on the trailer on impact. (2 marks)
- Ft = M(V – U)
F = M(V - U) = 30,000 (15 - 20)✓①
t 0.5
F = -300,000N or 300,000N✓①
- Ft = M(V – U)
- The common velocity. (3 marks)
- Give the reasons why a safety seat belt used in a vehicle; should have a wide surface area. (1 mark)
- To increase the area on which the force cuts to reduce pressure ✓①due to impulsive force.
- A boy throws a tennis ball vertically upwards from a truck moving at a constant velocity. Give the reason why the ball lands back exactly the same point where it was projected.
- The tape in figure below was obtained from an experiment using a ticker timer of frequency 50Hz. The tape was pulled by a trolley.
If the trolley that was pulling the tape was accelerating,-
- Show on the diagram, the direction of acceleration of the trolley. (1 Mark)
- Towards the left
- Calculate the acceleration of the trolley. (4 Marks)
- a = (v-u)/t
t = 1/50 = 0.02 s✓①
v = 0.08/0.02 = 4m/s✓①
u = 0.02/0.02 = 1m/s✓①
a = 4-1/0.02 x 6 = 3/0.12✓①
= 25m/s2
- a = (v-u)/t
- Show on the diagram, the direction of acceleration of the trolley. (1 Mark)
- A stone is allowed to fall freely from the top of a tower 60 metres high. At the same time, a second stone is thrown vertically upwards with a velocity of 20m/s from the ground. Find;
- The time taken by the two stones before they meet. (3 Marks)
- h = ut – ½ gt2 for the body falling freely OR UP S1 =1/2gt2
h = 20t – ½ x 10 x t2 (60 – h) = ½ gt2 S1+S2 =60
= 20t – 5t2✓① 60 – h = ½ x 10 x t2 1/2gt2+ Ut -1/2gt2=60
From h = 20t – 5t2 60 – h = 5t2✓①
Then Ut=60
60 – (20t – 5t2) = 5t2✓① t=3s
60 – 20t + 5t2 = 5t2
60/20 = 20/20 t DOWN S2= Ut -1/2gt2
t = 3s√1
- h = ut – ½ gt2 for the body falling freely OR UP S1 =1/2gt2
- The height at which the two stones meet. (2 Marks)
- h = ut – ½ gt2
= 20 x 3 – ½ x 10 x 32√1
= 60 – 45√1
=15m√1
- h = ut – ½ gt2
- The time taken by the two stones before they meet. (3 Marks)
-
-
-
- State Archimedes’ Principle. (1mark)
- Archimedes’ Principle states that when a body is partially or wholly immersed in a fluid, it experiences an up thrust equal to the weight of the fluid displaced
- Archimedes’ Principle states that when a body is partially or wholly immersed in a fluid, it experiences an up thrust equal to the weight of the fluid displaced
- Figure below shows a block of dimensions 2cm × 4cm × 12cm floating in a liquid of density 1250kg/m³
Find- The up thrust on the block. (3 marks)
- Up thrust= egh ✓1
2 × 4 × 8 × 1250 × 10✓1
100 100 100
= 0.8 N✓1
- Up thrust= egh ✓1
- The weight of the block. (1 mark)
- Weight of block = Up thrust
= 0.8 N
- Weight of block = Up thrust
- Given that gravitational pull is 10 N/Kg, calculate density of the block. (3 marks)
- Mass = weight/(gravitation pull) Mass = (0.8 )/10 =0.08kg✓1
Density = mass/volume Density = 0.08 kg/0.0000096 ✓1
=833.33kg/m3✓1
- Mass = weight/(gravitation pull) Mass = (0.8 )/10 =0.08kg✓1
- The up thrust on the block. (3 marks)
- State Archimedes’ Principle. (1mark)
-
-
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N.
- How much potential energy does the load gain. (2 marks)
- P.E = mgh
10 x 2 x 10√
= 200J√
- P.E = mgh
- How far does the effort end move in order to raise the load by 2m? (1 mark)
- Distance moved by effort = 2x2 = 4m√
- Distance moved by effort = 2x2 = 4m√
- How much work is done by the effort (2 marks)
- Work done = f x d √
100 x 4 = 400J √
- Work done = f x d √
- What is the efficiency of these pulleys? (2 marks)
- M.A x 100%
V.R
= 100 x ½ x 100 = 125
80 2
= 62.5%
- M.A x 100%
- If all the wasted energy is used to lift the bottom pulley, how much does the pulley weigh? (2 marks)
- 400 – 200 = 120
Mg = 200/h = 200/2 = 100N
- 400 – 200 = 120
- How much potential energy does the load gain. (2 marks)
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N.
-
- A stone of mass 450g is rotated in a vertical circle at 3 revolutions per second. If the string has a length of 1.5m, determine:
- The linear velocity. (2mks)
- V = ωr √1
V = 6π x 1.5
= 6 x 3.142 x 1.5
= 28.278 m/s √1
- V = ωr √1
- The tension of the string at position A (2 marks)
- mv2 = TA + mg √1
r
∴ TA= mv2 – mg
r
= 0.45 x 28.2782 – 0.45 x 10 √1
1.5
= 0.45 x 799.645 – 0.45 x 10
1.5
= 239.894 – 4.5 = 235.394N √1
- mv2 = TA + mg √1
- The tension of the string at position B (2 marks)
- Mv2 = TB – mg
r
TB = mv2 + mg
r
= 239.894 + 4.5 √1
= 244.394N √1
- Mv2 = TB – mg
- The linear velocity. (2mks)
- A stone is whirled with uniform speed in horizontal circle having radius of 10cm. it takes the stone 10 seconds to describe an arc of length 4cm.
- The angular velocity ω. (2 marks)
- ∆θ in radians = s/r = 4/10 = 0.4radians
Angular velocity, ω = ∆θ = 0.4 √1
∆t 10
= 0.04radians per second √1
- ∆θ in radians = s/r = 4/10 = 0.4radians
- The period time T. (2 marks)
- T = circumference
Speed
= 2πr V = ωr
V
= 2πr
ωr
= 2π
ω
= 2 x 3.142 √1
0.04
= 157.1 seconds √1
- T = circumference
- The angular velocity ω. (2 marks)
- State TWO factors affecting centripetal force. (2 marks)
- Mass of the object √1
- Angular velocity of the object√1 (any two)
- Radius of the path √1
- A stone of mass 450g is rotated in a vertical circle at 3 revolutions per second. If the string has a length of 1.5m, determine:
-
- State what is meant by the term specific latent heat of vaporization? (1 mark)
- Specific latent heat of vaporization is the quantity of heat required to change a unit mass of a substance from liquid to vapour at constant temperature.
- Specific latent heat of vaporization is the quantity of heat required to change a unit mass of a substance from liquid to vapour at constant temperature.
- In an experiment to determine the specific latent heat of vaporization of water, steam at 1000C was passed into water contained in a well lagged copper calorimeter. The following measurements were made.
Mass of calorimeter =40g
Initial mass of water =80g
Final mass of calorimeter + water + condensed steam = 123g
Initial temperature of water + calorimeter = 50 C
Final temperature of mixture = 300C
(specific heat capacity of water=4200JKg-1K-1 and specific heat capacity of copper=390 JKg-1K-1.}
Determine:- Mass of the condensed steam. (1 mark)
- 123 – 120 = 3g
= 0.003Kg
= 3.0x10-3Kg
- 123 – 120 = 3g
- Heat gained by calorimeter alone (2 marks)
- Heat gained by calorimeter
Q = mc∆θ
= 0.04 x 390 x 25
= 390J
- Heat gained by calorimeter
- Heat gained by water only. (2 marks)
- Heat gained by water
Q = mc∆θ
= 0.08 x 4200 x 25
= 8400J
- Heat gained by water
- Given that L is the specific latent heat of evaporation of steam
- Write an expression for the heat given out by steam. (1 mark)
- ML+ Mc∆θ =8790J
- ML+ Mc∆θ =8790J
- Determine the value of L (3 marks)
- 0.003L+882=8790
(0.003×4200×70)=882J
0.003L=7908J/Kg
=2.636 x 106J/Kg
- 0.003L+882=8790
- Write an expression for the heat given out by steam. (1 mark)
- Mass of the condensed steam. (1 mark)
- State what is meant by the term specific latent heat of vaporization? (1 mark)
Download Physics Paper 1 Questions and Answers - MECS Cluster Joint Pre Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students