Instructions to candidates
- Write your name and index number in the spaces provided above.
- Sign and write the date of examination in the spaces provided above.
- This paper consists of two sections I, II.
- Answer all the questions in section 1 and any five questions from section II.
- All working and answers must be written on the question paper in the spaces provided below each question.
- Show all steps in your calculations, giving answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used.
QUESTIONS
SECTION 1 (50MARKS)
- Use logarithms to evaluate (4mks)
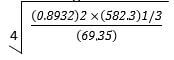
- A rectangular card measures 5.3cm by 2.5cm. find
- The absolute error in the area of the card. (2mks)
- The relative error in the area of the card (2mks)
- Solve the equation (4mks)
Sin (2x +10)º=-0.5 for 0º ≤ x≤ 360º - In a transformation, an object with an area of 52cm2 is mapped onto an image whose area is 30cm2. Given that the matrix of the transformation is
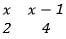find the value of x (3mks) - Simplify
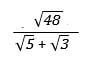leaving your answer in the form of a√b + c where a, b and c are integers. (3mks) - A customer deposited sh 14000 in a saving account. Find the accumulated amount after one year if interest was paid at 12% p.a compounded quarterly (3mks)
- Expand (1+x)5, hence use the expansion to estimate (1.04)5 correct to 4 decimal place (3mks)
- Find the centre and the radius of circle whose equation is (3mks)
x2+4x+y2-5=0 - Make d the subject of the formula (3mks)
P=1/2mn2-gd2
n - In what proportion should grades of sugar costing sh 45 and sh 50 per kg be mixed in order to produce a blend worth sh 48 per kg (3mks)
- Simplify the expression (3mks)
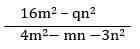
- Find the equation of the tangent to the curve (3mks)
y=2x2 at (2, 3) - Use matrix method to solve the given simultaneous equation (3mks)
3x+y=7
5x+2y=12 - The sum of n terms of the sequence 3, 9, 15, 21 ... is 7500. Determine the value of n (3mks)
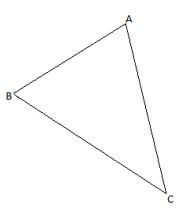
- The figure below (not drawn to scale) shows a triangle ABC in which AB=6cm, BC=9cm, AC=10cm. calculate the radius of the circle touching the three vertices of the triangle. (3mks)
- The point p (40ºS, 45ºE) and point Q (40ºS, 60ºW) are on the surface of the earth. Calculate the shortest distance along a circle of latitude between the two points. (3mks)
- The table below shows monthly income tax rates.
A civil servant earns a monthly salary of sh 20 000 and is provided with a house at a normal rent of sh 700 per month.Monthly taxable pay K£
Rate of tax sh per K£
1-342
343-684
685-1026
1027-1368
1369-1710
Over 1710
2
3
4
5
6
7
- calculate the civil servant taxable pay in K£ (4mks)
- Calculate the total tax (4mks)
- If the employee is entitled to a tax relief of sh 600 per month. What is the net tax paid? 2mks)
- In an agricultural research centre, the length of a sample of 50 maize cobs were measured and recorded as shown in the frequency distribution table below.
CalculateLength in cm
Number of cobs
8-10
11-13
14-16
17-19
20-22
23-25
4
7
11
15
8
5
- The mean (2mks)
-
- the variance (5mks)
- The standard deviation (3mks)
- In the diagram shown below O is the centre of the circle, angle RTV=1500,and angle RST=500,
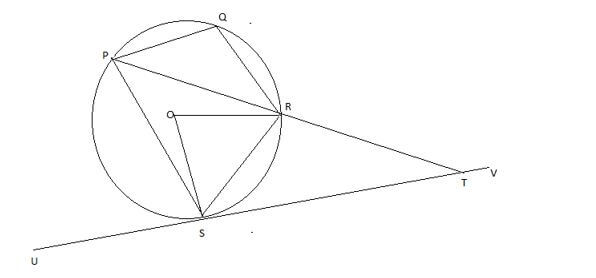
- Calculate the size of
- <ORS (2mks)
- <USP (1mk)
- <PQR (2mks)
- Given that RT =7cm and ST=9cm, calculate to 3.s.f
- The length of line PR (2mks)
- The radius of the circle (3mks)
- Calculate the size of
- The position of two towns A and B on the earth surface are (36ºN, 49ºE) and (36ºN, 131ºW) respectively
- Find the difference in longitude between town A and town B (2mks)
- Given that the radius of the earth is 6370km calculate the distance between town A and B (4mks)
- Another town C is 840km east of town B and on the same latitude as towns A and B. find the longitude of town C (4mks)
- The distance sm from a fixed point O, covered by a particle after ts is given by the equation
S=t3-6t2+9t+5- Calculate the gradient to the curve at t=0.5s (3mks)
- Determine the values of s at the maximum and minimum turning points of the curve. (4mks)
- On the space provided sketch the curve of s=t3-6t2+9t+5 (3mks)
- In the figure below OQ =a and OB=b. m is the midpoint of OA and AN:NB =2:1
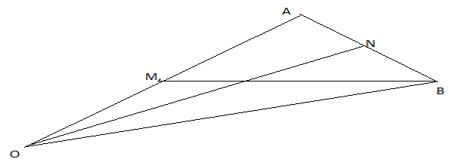
- Express in terms of a and b
- BA (1mk)
- BN (1mk)
- ON (2mks)
- Given that BX=hBM and OX=KON determine the values of h and k (6mks)
- Express in terms of a and b
-
- Complete the table below, giving the values correct to 1 d.p (2mks)
X0
0
40
80
120
160
200
240
2sin (x+20)0
0.7
2.0
0.0
-2.0
√3 cos x
1.7
1.3
-0.9
-1.6
- On the grid provided, using the same scale and axes, draw the graphs of y=2sin (x+20)º and y=√3 cos x for 0≤x≤ 240º (5mks)
- Use the graphs drawn in (b) above to determine:
The values of x for which 2 sin (x+20)º =√3 cos x (2mks)
The difference in the amplitudes of y=2sin(x+20) and y=√3 cox x (1mk)
- Complete the table below, giving the values correct to 1 d.p (2mks)
- The probabilities that a husband and wife will be a live 25 years from now are 0.7 and 0.9 respectively. Find the probability that in 25 years time;
- Both will be a live (2mks)
- Neither will be a live (3mks)
- One will be a live (2mks)
- At least one will be a live (3mks)
MARKING SCHEME
SECTION 1 (50MARKS)
- Use logarithms to evaluate (4mks)
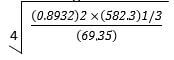
No std log 0.8932 8.932 x 10-1 1.9509 x 2 582.3 5.823 x 102 2.7651
309.36 0.935 x 101 1.8410 - A rectangular card measures 5.3cm by 2.5cm. find
- The absolute error in the area of the card. (2mks)
max V 5.35 min 5.25 max 2.55 min 2.45
max A - min A = M1
2
13.3875 - 12.8625
2
= 0.2626% - The relative error in the area of the card (2mks)
- The absolute error in the area of the card. (2mks)
- Solve the equation (4mks)
Sin (2x +10)º=-0.5 for 0º ≤ x≤ 360º
2x + 10 = sin-1-0.5
= -30º
2x + 10 = 210º, 330º, 570º, 690º
x = 100º, 160º, 280º, 335º - In a transformation, an object with an area of 52cm2 is mapped onto an image whose area is 30cm2. Given that the matrix of the transformation is 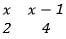find the value of x (3mks)
ASF = 30/52
= 15/26 = 4x - 2x + 2
15/26 = 2x + 2
x = -37/26 - Simplify 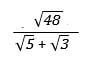leaving your answer in the form of a√b + c where a, b and c are integers. (3mks)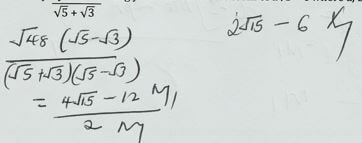
- A customer deposited sh 14000 in a saving account. Find the accumulated amount after one year if interest was paid at 12% p.a compounded quarterly (3mks)
A = 14000 (1 + 12/100 x 1/4)4
= 14000(1.03)4
= 15757 - Expand (1+x)5, hence use the expansion to estimate (1.04)5 correct to 4 decimal place (3mks) r = 3
- Find the centre and the radius of circle whose equation is (3mks)
x2+4x+y2-5=0 - Make d the subject of the formula (3mks)
P=1/2mn2-gd2
n
2pn - mn3 = 2gd2
d2 = mn3 - 2pn
2q - In what proportion should grades of sugar costing sh 45 and sh 50 per kg be mixed in order to produce a blend worth sh 48 per kg (3mks)
let a:b = ratio
45a + 50b = 48
a + b
45a - 48a = 48b - 50b
a:b = 2:3 - Simplify the expression (3mks)
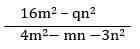
N:(4m - 3n)(4m + 3n)
D: 4m3 - 4mn + 3mn - 3n2
4m(m - n) + 3n(m - n)
(4m + 3n)(m - n)
= 4m - 3n
m - n - Find the equation of the tangent to the curve (3mks)
y=2x2 at (2, 3)
dy/dx = 4x
at x = 2
m = 2(4)
= 8
(x,y)(2,3)
m = 8
y - 3 = 8
x - 2 1
y - 3 = 8 x -16
y = 8x + 15 - Use matrix method to solve the given simultaneous equation (3mks)
3x+y=7
5x+2y=12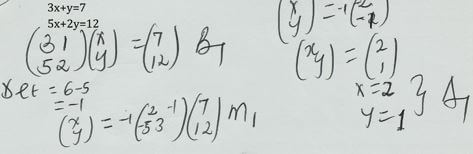
- The sum of n terms of the sequence 3, 9, 15, 21 ... is 7500. Determine the value of n (3mks)
n/2(2a(n - 1)d) = 7500
n/2(6 + (n - 1)6) = 7500
6n + 6n2 = 15000
6n2 = 15000
n2 = 2500
n = 50 - The figure below (not drawn to scale) shows a triangle ABC in which AB=6cm, BC=9cm, AC=10cm. calculate the radius of the circle touching the three vertices of the triangle. (3mks)
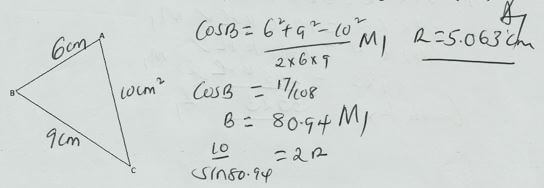
- The point p (40ºS, 45ºE) and point Q (40ºS, 60ºW) are on the surface of the earth. Calculate the shortest distance along a circle of latitude between the two points. (3mks)
Ò = 105º
= 105 x 2 x 22 x 6370 cos 40
360 7
= 8946 km - The table below shows monthly income tax rates.
A civil servant earns a monthly salary of sh 20 000 and is provided with a house at a normal rent of sh 700 per month.Monthly taxable pay K£
Rate of tax sh per K£
1-342
343-684
685-1026
1027-1368
1369-1710
Over 1710
2
3
4
5
6
7
- calculate the civil servant taxable pay in K£ (4mks)
20000 + 15/100 x 20000 - 700
22300/20 = 1115t - Calculate the total tax (4mks)
ans = 3523 - If the employee is entitled to a tax relief of sh 600 per month. What is the net tax paid? 2mks)
3523
- 600
29231
- calculate the civil servant taxable pay in K£ (4mks)
- In an agricultural research centre, the length of a sample of 50 maize cobs were measured and recorded as shown in the frequency distribution table below.
CalculateLength in cm
Number of cobs
x x2 fx fx2 8-10
11-13
14-16
17-19
20-22
23-25
4
7
11
15
8
5
9
12
15
18
21
24
81
144
225
324
441
576
36
84
165
270
168
120
324
1008
2475
4860
3528
2880
∑x = 843 ∑fx = 15075 - The mean (2mks)
= 16.86 -
- the variance (5mks)
= 17.25 - The standard deviation (3mks)
= 4.153
- the variance (5mks)
- The mean (2mks)
- In the diagram shown below O is the centre of the circle, angle RTV=1500,and angle RST=500,
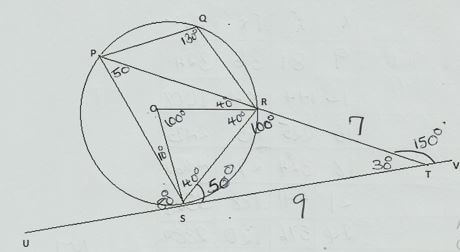
- Calculate the size of
- <ORS (2mks)
= 40º - base < s isosceles angles are equal - <USP (1mk)
= 80º - alternate segments theorem - <PQR (2mks)
= 130º - opposites <s a cycle quadrilateral add up to 180º
- <ORS (2mks)
- Given that RT =7cm and ST=9cm, calculate to 3.s.f
- The length of line PR (2mks)
(x + 7)7 = 92 7x + 49 = 81 7x = 22
x = 3.142 - The radius of the circle (3mks)
PR = 7 + 3.142
= 10.142
3.142 = 2R
sin 50
R = 2.05cm
- The length of line PR (2mks)
- Calculate the size of
- The position of two towns A and B on the earth surface are (36ºN, 49ºE) and (36ºN, 131ºW) respectively
- Find the difference in longitude between town A and town B (2m
= 49 + 131
180= ) - Given that the radius of the earth is 6370km calculate the distance between town A and B (4mks)
= 16196 km - Another town C is 840km east of town B and on the same latitude as towns A and B. find the longitude of town C (4mks)
= 121.66ºW
- Find the difference in longitude between town A and town B (2m
- The distance sm from a fixed point O, covered by a particle after ts is given by the equation
S=t3-6t2+9t+5- Calculate the gradient to the curve at t=0.5s (3mks)
ds/dt = 3t2 - 12t + 9
= 3(1/4) - (12)1/2 + 9
= 3/4 - 6 + 9
= 15/4 - Determine the values of s at the maximum and minimum turning points of the curve. (4mks)
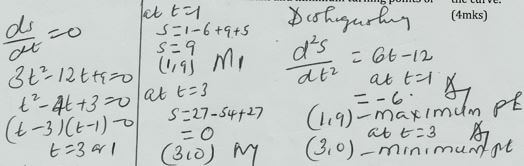
- On the space provided sketch the curve of s=t3-6t2+9t+5 (3mks)
intercepts at t = 0 at s = s
=> (0,5) min (3,0) max(1,9)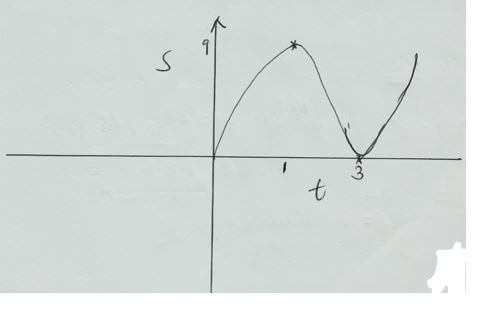
- Calculate the gradient to the curve at t=0.5s (3mks)
- In the figure below OQ =a and OB=b. m is the midpoint of OA and AN:NB =2:1
- Express in terms of a and b
- BA (1mk)
b + a - BN (1mk)
1/3b + 1/3a - ON (2mks)
a + 2/3AB = 1/3a + 2/3b
- BA (1mk)
- Given that BX=hBM and OX=KON determine the values of h and k (6mks)
k = 3/2h
- Express in terms of a and b
-
- Complete the table below, giving the values correct to 1 d.p (2mks)
X0
0
40
80
120
160
200
240
2sin (x+20)0
0.7
1 2.0
0.0
-2.0
√3 cos x
1.7
1.3
-0.9
-1.6
- On the grid provided, using the same scale and axes, draw the graphs of y=2sin (x+20)º and y=√3 cos x for 0≤x≤ 240º (5mks)
- Use the graphs drawn in (b) above to determine:
The values of x for which 2 sin (x+20)º =√3 cos x (2mks)
The difference in the amplitudes of y=2sin(x+20) and y=√3 cox x (1mk)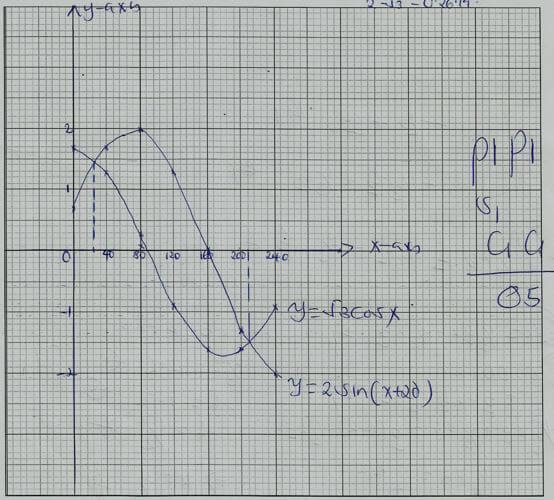
- Complete the table below, giving the values correct to 1 d.p (2mks)
- The probabilities that a husband and wife will be a live 25 years from now are 0.7 and 0.9 respectively. Find the probability that in 25 years time;
- Both will be a live (2mks)
0.7 x 0.9 = 0.63 - Neither will be a live (3mks)
0.3 x 0.37 = 0.111 - One will be a live (2mks)
(0.7 x 0.37) + (0.9 x 0.3) = 0.529 - At least one will be a live (3mks)
0.529 x 0.63 = 0.33327
- Both will be a live (2mks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 2 Questions and Answers - Asumbi Girls Highschool Pre-Mock Exams May - June 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
