Mathematics Paper 1 Questions and Answers - Momaliche Joint Pre Mock Exams 2022

QUESTIONS
SECTION I

1. Without using calculators or mathematical tables, evaluate leaving your answer in standard form. (3mks)
     1.33 × 0.51  
   0.19 × 0.0017 
2. Three bells are programmed to ring after an interval of 15 minutes, 25 minutes and 50 minutes. If they all rang together at 6.45am, when will they next ring together? (3mks) 
3. The volumes of two similar solid cylinders are 1920cm³ and 810cm³. If the area of the curved surface of the smaller cylinder is 300cm², find the area of the curved surface of the larger cylinder. (4mks)
4. Solve for x in the equation (3mks)
   (3^2x)³ = 81 × 9⁴
5. Class of 30 students uses 75 pencils in a term. If the number of students is reduced to 24, how many pencils are likely to be used in a term? (2mks)
6. An empty 300ml bottle has a mass of 270g. Calculate the mass of the bottle when it is full of a liquid whose density is 1.1g/cm³. (3mks)
7. Simplify 4x - 20 (3mks)
                  5 - x 
8. The shaded region in the figure below shows a section of a road on a roundabout. Calculate the area in cm². (use π=3.142) (3mks)
   
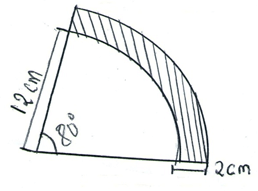
9. Solve the inequalities and represent your solution on a single number line.
   x - 5 ≤ 3x - 8 < 2x - 3 (3mks)
10. Tourists visits Kenya and changes $400 to ksh. At the end of the holiday, she has only ksh. 1450 left. How many dollars did she spend in the holiday if the exchange rate is as per the table below.
    

    Currency	Buying ksh	Selling Ksh
    1US dollar $	79.25	81.50

    (3mks)
11. Use tables of squares, square root and reciprocal only to evaluate. (4mks)
    0.06458^½ + (    2    )²
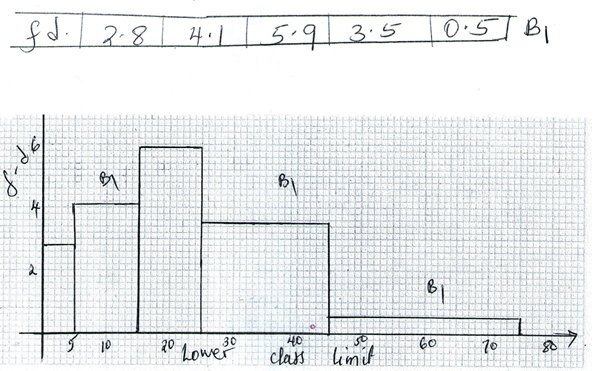
                       0.4327 
12. Every week, the age of people who attend a cinema is recorded. In a particular week the data was as shown in the table below.
    

    Age (year)(x)	0 ≤ x< 5	5 ≤ x < 15	15 ≤ x < 25	25 ≤ x < 45	45 ≤ x < 75
    No of people	14	41	59	70	15

    On the grid provided, draw a histogram to represent the distribution.
    Scale: 1cm to represent 5 units on horizontal axis
    2cm to represent 2 units on vertical axis. (4mks)
13. If p = (³₄), q = (^-2₁) and c =(¹³₂₁) Find the scalar m to satisfy the equation 5p + mq = c (3mks)
14. Find the sum of interior angles of a regular polygon with 18 sides. (2mks)
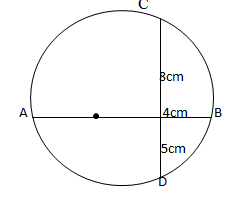
15. In the figure below, O is the centre of the circle. Chords AB and CD intersect at X. Given that CX = 8cm, XD = 5cm and XB = 4cm, calculate the length of AX and hence find the radius of the circle. (3mks)
    
16. Use logarithm tables to evaluate(4mks)
    ∛(1.42 × 0.004623)
               log⁴

SECTION II
Answer any five questions only

17. A sales lady dealing in shoes earn a basic salary of shs 30,000. In addition she is paid commission on the sales of shoes as follows.
    Commission
    For sales up to shs 100,000 0%
    For sales above shs 100,000
    1. For first 50,000 4%
    2. For next 50,000 5%
       Any amount above 200,000 10%
       On a certain month she sold 200 pair of shoes marked at shs 1200 a pair at a discount of 5%.
       1. Calculate the total sales for the month. (2mks)
       2. Calculate her total earning for that month. (4mks)
       3. If the next month her basic salary was increased by 10%. If she earned a total of sh. 39,160: Determine
          
          1. Her total sales for the month. (2mks)
          2. The number of pairs of shoes she sold that month. (2mks)
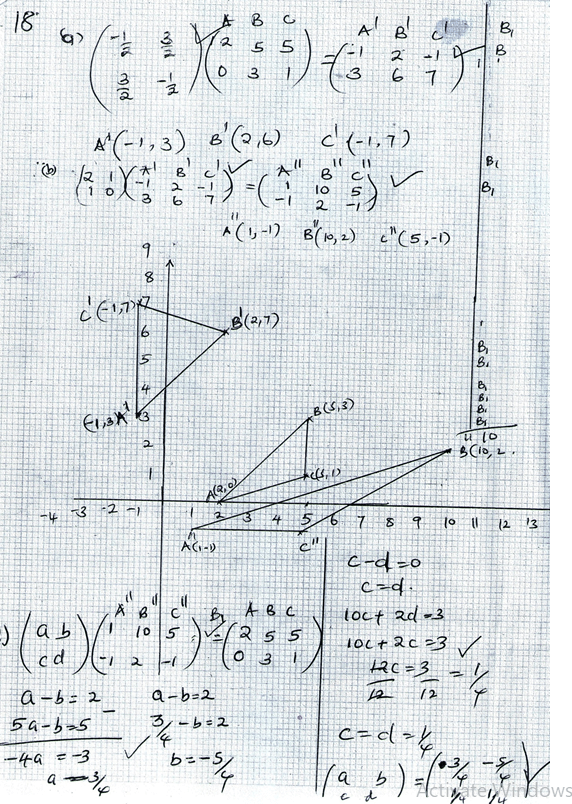
18. The vertices of the triangle shown below are
    A(2,0), B(5,3) and C(5,1)
    1. Find the coordinates of triangle A^I B^I C^I the image of triangle ABC after a transformation by the matrix T= 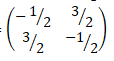(2mks)
    2. Find the coordinates of triangle A^II B^II C^II, the image of triangle A^I B^I C^I after a transformation by the matrix S= 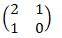(2mks)
    3. Draw both triangle A^I B^I C^I and triangle A^II B^II C^II on the same grid as triangle ABC. (2mks)
    4. Determine the single matrix that can map triangle A^II B^II C^II on to triangle ABC (4mks)
19.      
    1. Using a ruler and a pair of compases only, construct triangle PQR in which QR = 1.5CM, PR = 2.2cm and angle PRQ = 120º (3mks)
    2. Measure PQ and angle PQR (2mks)
    3. Construct the perpendicular bisector QR and PR (2mks)
    4. Draw the circumscribed circle of triangle PQR (2mks)
    5. Measure the radius of the circle. (1mk)
20. In the figure below PQR and QUV are straight lines. QS are parallel to TV. Angles SQR = 40º and TQV =55º
    O – is the centre of circle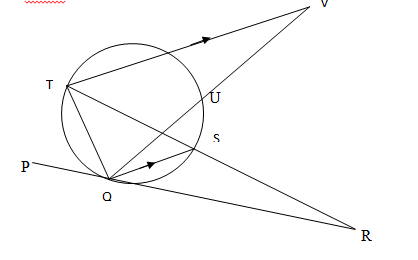
    
    
    1. Find the following angles giving reasons in each case
       
       1. <QTS (2mks)
       2. <QRS (2mks)
       3. <QVT (2mks)
       4. <QUT (2mks)
    2. Given that QR = 8cm and SR=4cm, find the radius of the circle. (2mks)
21. Two towns A and B are 80km apart. James started cycling from Town A to town B at 10.00am at an average speed of 40kmhr^-1. Mutuku started his journey from town B to A at 10.30am and travelled by car at an average speed of 60kmhr^-1.
    1. Calculate
       1. The distance from A when James and Mutuku met. (5mks)
       2. Time of the day when the two met. (2mks)
    2. Kimeli started cycling from town A to town B at 10.21 am. He met Mutuku at the same time as James did. Determine Kimeli’s average speed. (3mks)
22. A straight line L1 whose equation is 3y – 2x = -2 meets the x – axis at R
    1. Determine the coordinates of R. (2mks)
    2. A second line L₂ is perpendicular to L₁ at R. Find the equation of L₂ in the form
       y = mx+c where m and c are constants. (3mks)
    3. A third line L₃ passing through (-4, 1) is parallel to L1. Find
       
       1. The equation of L₃ in the form y=mx+c where m and c are constants. (2mks)
       2. The coordinates of points S at which L₃ intersects L2 (3mks)
23.        
    1. Complete the table below for the function
       Y = x³ + 4x² + 7x + 6 (give y values correct to 1dp) (2mks)
       

       x	-4.5	-4	-3.5	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1.0	1.5	2
       x3	-91.1	-64	42.9	-27		-8		-1	-0.1	0	0.1	1	3.4	8
       4x2	81	64	49	36		16		4		0	1	4	9	16
       7x	-31.5	-28	24.5	-21		-4		-7	3.5	0	3.5	7.5	10.5	14
       6	6	6	6	6	6	6	6	6	6	6	6	6	6	6
       y	-35.6	-22.0	-22.4	-6.0		0.0		2.0	3.4	6	10.6	18.0		44

    2. Draw the graph of y =x³ + 4x² + 7x + 6 for -4.5≤ x ≤ 2 on the grid provided below (using 1cm rep 0.5 on x- axis (1cm rep 5 on y- axis) (3mks)
    3. Use your graph to solve the simultaneous equations (3mks)
       
       1. y=x³+ 4x²+7x+6
       2. y=10x + 15
    4. Find a cubic equation in x whose roots are the x values you found in c above. (1mk)
    5. From your graph state the root of x³+ 4x²+ 7x + 6=0 (1mk)
24. The diagram below shows a wooden solid consisting of a cylindrical part of radius 3.5cm and a conical part of radius 4.2cm. (use π=²²/₇)
    
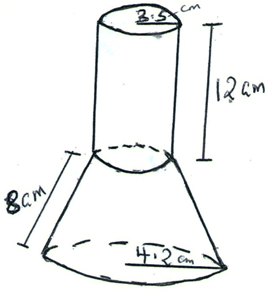
    Find correct to two decimal places.
    1. The surface area of the conical part. (5mks)
    2. The volume of solid. (5mks)

MARKING SCHEME

1.   1.33 × 0.51  
   0.19 × 0.0017
   133 x 51 x 100
       19 x 17
   2100
   2.1 x 10³
2. LCM of 15, 25, 50
   15 = 3 x 5 
   25 = 5²
   50 = 2 x 5²
   LCM = 2 x 3 x 5² = 150min
   Time of day = 6.45am
   150min = 2h 30mins
   6.45 + 2.30 = 9:15am
3. VSF = 1920 = 64
               810     27
   LSF = ³√⁶⁴/₂₇ = ⁴/₃
   ASF = (⁴/₃)² = 16/9
   ¹⁶/₉ = x/300
   x = 16 x 300 = 533.33 or 533¹/₃
             9
4. (3^2x)³ = 81 x 9⁴ 
   3^6x = 3⁴ x 3⁸
   3^6x = 3¹²
   6x = 12
   x = 2
5. New ratio 24:30
   ²⁴/₃₀ = ^x/₇₅ 
   ²⁴/₃₀ x 75 = x
   x = 60
6. Volume = 300ml = 300cm³
   Density = 1.1g/cm³
   Mass of liquid = 1.1 x 300
   =330g
   Mass of bottle = 330 + 270
   = 600g
7. 4(x - 5)
     5 - x
   -4(5 - x)
    (5 - x)
8. Area = ^θ/₃₆₀πR² - ^θ/₃₆₀πr
   ^θ/₃₆₀π(R² - r²)
   ⁸⁰/₃₆₀ x 3.142(14² - 12²)
   0.6982(196 - 144)
   0.6982 x 52 = 36.30
   or
   ⁸⁰/₃₆₀ x 3.142 x 14² = 136.85
   ⁸⁰/₃₆₀ x 3.142 x 12² = 100.5
   = 36.30
9. x - 5 ≤ 3x - 8 < 2x
   x - 5 ≤ 3x - 8
   -5 + 8 ≤ 2x
   3 ≤ 2x
   1.5 ≤ x
   3x - 8 < 2x - 3
   x < 5
   1.5 ≤ x < 5
   
10. 400 x 79.25 = ksh31700
    amount spent = 31700 - 1450
    = sh30250
    in dollars = 30250 = $371A
                        81.5
11. (0.06458)^½ +        2 ²
                         0.4327
    (6.458 x 10^-2)½ + 2(4.327 x 10^-1)
    (2.5415 x ¹/₁₀) + 2(0.2311 x 10) = (4.622)²
    0.25415 + 21.363 = 21.61715
12.     
    
13. 5p + mq = c
    5 = (³₄), m = (^-2₁) =(¹³₂₁)
    15 - 2m = 13
    2 = 2m
    1 = m
14. (2n - 4)90
    [(18) - 4]90 = 32 x 90 = 2880º
15. Ax . xB = Cx . xD
    Ax =8 x 5= 10
             4
    Radius =10 + 4= 7
                      2
16. 
    
    0.2217 ← 2.217 x 10-1 ← 1.3458
17.      
    1. 0.95 x 1200 x 200 = 228000
    2. commission = 228000 - 100000 = 128000
       (0.04 x 50000) + (0.05 x 50000) + (0.1 x 28000)
       =sh 73000
       total = sh(30000 + 7300) = sh 37300
    3.      
       1. Total sales 
          commission
          39160 - 1.1 x 30000 = 6160
          6160 - (2000 + 2500) = 1660
          100 x 1660 = 16600
          100
          = 200000 + 16600 = sh216600
       2. pairs sold 
              216600    = 190pairs
          0.95 x 1200
18.    
    
19.        
    1.      
       
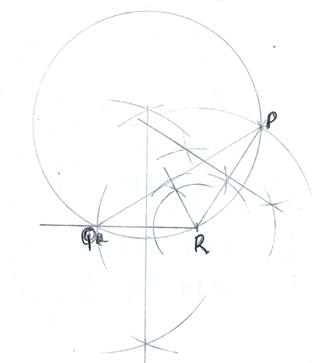
    2. Measure distance PQ = (6.8 ± 0.1)cm
       <PQR = 32 ± 1%
    3. constructing perpendicular bisectors
       PR B QR B1 
    4. Locating center O draw correct circle
    5. Measuring radius (4.1 ± 0.1)cm
20.      
    1.    
       1. <QTS  = 40 ngle in alternate segment
       2. TQS  = 90 angle ina semicircle 
          40 +(90 + 40) + <QRS = 180
          <QRS = 10
       3. TSQ = 50; RTV = 50 (altefrnate)
          QVT = 180 - (55 + 90) = 35
       4. QUT  = 50 is subtended by same arc
    2. 4 x RT = 64 RT = 16
       TS = 16 - 4 = 12 
       r = 6
21. 
            
    1.          
       1. Distance covered by James in 30mins
          D = S x T = 40km/h x ½ = 20km
          relative speed (40 + 60) kmh-1 = 100kmh^-1
          Time taken by both to react = D/S
          = 60km/100kmh^-1 = ³/₅h or 36 mins
          In ³/₅ hrs James had gone what distance
          D = Sx T = ³/₅hrs x 40kmh^-1= 24km
          Distance from A to the meeting point
          =  (20 + 24)km = 44km
       2. Time of the day when the two met
          (10.30 + 36min) = 11.06am
    2. Distance(44km) meeting point
       Time taken by Kimeli (11.06 - 10.21) = 45mins or hrs
       S = ^D/_T = ⁴⁴/_¾ = 44 x ⁴/₃ = 58²/₃kmh^-1
22.        
    1. At x axis y = 0
       y = ²/₃x - ²/₃ 
       ²/₃ x - ²/₃ = 0
       ²/₃x = ²/₃
       x = 1 R(1,0)
    2. L₂
       m1 x m₂ = -1
       ²/₃m₂ = -1
       m₂ = -³/₂
       y - 0 = -³/₂
       x - 1
       2(y - 0) = -3(x - 1)
       2y = -3x + 3
       y = -³/₂x + ³/₂
    3.      
       1. L1 and L3 are parallel
          L3 m = ²/₃  
          y - 1 = ²/₃
          x + 4
          3(y - 1) = 2(x + 4)
          3y - 3 = 2x + 8 
          ^3y/₃ = ^2x/₃ + ¹¹/₃
          y = ²/₃x +¹¹/₃
       2. L3 L2 intersect at S
          ²/₃x + ¹¹/₃ = ^-3/₂x + ³/₂
          ²/₃x + ³/₂x = ³/₂ - ¹¹/₃
          4x + 9x = 9 - 22
               6            6 
          ¹³/₆x = -¹³/₆
          x = -1
          -³/₂(-1) + ³/₂ = ⁶/₂ = 3
          S(-1,3)
23.      
    1.      
       

       x	-4.5	-4	-3.5	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2
       y	-35.6	-23.0	-12.4	-6.0	-2.1	0.0	1.1	2.0	3.4	6.0	10.6	18.0	28.9	44

    2.      
       
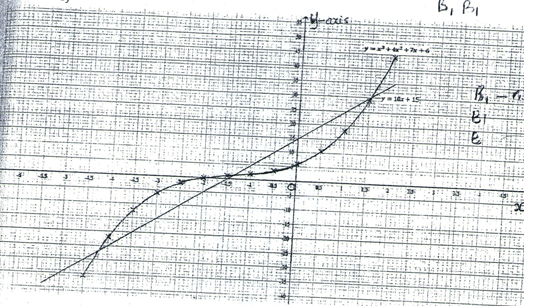
    3. The roots are x = 1.55 when y = 30.5
       x = -1.35 when y = 1.5 and x = -4.2 hwen y = -27
    4. x³ + 4x² + 7x + 6 = 10x + 15
       required equation : x³ + 4x² - 3x - 9 = 0
    5. The root is x = -2
24. 
    
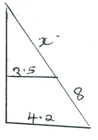
    4.2 = x + 8
    3.5      x
    4.2x = 3.5x + 28
    x = 40
    L = 48  L = 40
    S A of conical part
    π(RL - rl) + πr^{2
    22}/₇ (4.2 x 48 - 3.5 x 40) + ²²/₇ x 4.2 x 4.2
    = 193.6 + 55.44
    = 249.04cm²
    H = √48² - 4.2² = 47.82
    h = √40² - 3.5² = 39.85
    ¹/₃ x ²²/₇ (4.22 x 47.8 - 3.5² x 39.85) + ²²/₇ x 3.5² x 3.5 x 12
    = 372.31 + 462
    = 834.31
    = 1/3 x ²²/₇ [843.192 - 488.1625] + ²²/₇ x 35-2 x 12
    = ²²/₂₁[355.0295] + 462
    = 371.94 + 462
    = 833.94cm³