QUESTIONS
SECTION I
- Solve the quadratic equation by completing the square method.
x2 – 7x + 10 = 0 (3mks) - Simplify √5- √3 by rationalizing the denominator. (2mks)
√5+ √3 - Grade x rice costs shs 75 per kg and grade y rice costs shs 50 per kg. The two grades are mixed in the ratio such that the blend costs sh 70 per kg. Find the ratio in which grade x rice was mixed with grade y rice. (3mks)
- Given that A = ∜d-c2g make c the subject of the formula. (3mks)
b+c2f - Solve the equation 2 sin (3x + 60) = 1 for 0º ≤ x ≤ 180º (3mks)
-
- Expand and simplify (2 – x)8 up to 4th term. (2mks)
- Use the simplified expression in (a) above to estimate the value of (1.99)8 giving your answer correct to 4 significant figures. (2mks)
- Solve the equation 2 + log3 (2x -7) = log3(5x - 7) . (3mks)
-
- Construct a triangle ABC in which AB is 2.2cm, BC is 3.5cm and angle ABC is 60º(2mks)
- A point D moves such that it is on the same side of BC as A. Construct the locus of D such that the area of ΔABC = area of ΔBCD. (2mks)
- The equation of a circle is x2 + y2 – 6x + 8y – 11 = 0. Find the coordinates of the centre of the circle and its radius. (3mks)
- The length of a rectangle is 8.3 cm and its width is 5.45cm. Calculate
- The relative error in area of the rectangle (3mks)
- The percentage error in area (1mk)
- A triangle xyz whose area is 15.3cm2 mapped onto Δx1y1z1 by a transformation whose matrix is m =
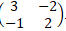 . Find the area of Δx1y1z1 .(3mks)
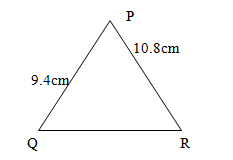
. Find the area of Δx1y1z1 .(3mks) - Solve the triangle (3mks)
- Fifteen men working at the rate of 9 hours per day take 20 days to complete a job. Find the number of days 27 men would take to complete the same job working at the rate of 10 hours a day. (3mks)
- The 5th term of an arithmetic sequences is 71 and the 7th term is 59. Find
- The first term and the common difference. (2mks)
- The 10th term (2mks)
- Use matrix methods to solve the simultaneous equations. (3mks)
3x – 4y = 2
6x + y = 13 - Factorise: 2x2 – x – 10 (2mks)
SECTION (II) (50MARKS)
- The following table shows the distribution of marks obtained by 50 students of a certain school.
Marks 45-49 50-54 55 - 59 60- 64 65 - 69 70-74 75- 79 No. of students 3 9 13 15 5 4 1 - State the modal class (1mk)
- By using an assumed mean of 62, calculate
- The mean (5mks)
- The standard deviation (4mks)
- The figure below is a triangle OAB, where OA = a and OB = b. A point R divides AB in the ratio 2:5 and a point T divides OB in the ratio 1:3. OR and AT intersect at D.
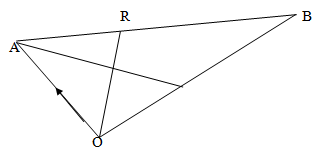
- Find in terms of a and b
- BT (1mk)
- OR (2mks)
- AT (1mk)
- Given that AD = KAT and RD = hRO where k and h are scalars. Find the values of k and h, hence express AD in terms of a and b (5mks)
- Find in terms of a and b
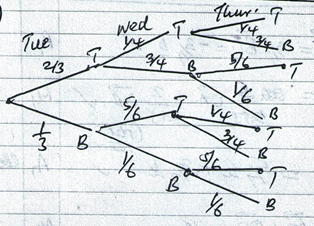
- John travels to work by either boda-boda or by tuk-tuk. If he travel by tuk-tuk on every one day, there is a probability of 0.75 that he travels by a boda boda the following day. If he travels by a boda boda on any one day, then he travels by tuk-tuk the following day with a likelihood of 5/6 . There is a chance of 2/3 that he travels by tuk-tuk on Tuesday.
- Draw a tree diaagram to illustrate the possible outcomes in 3 days. (2mks)
- Find the probability that he travel by;
- Boda-boda on Wednesday (2mks)
- Tuk-tuk on Wednesday (2mks)
- Boda – boda on Thursday (3mks)
- Tuk-tuk on Thursday (1mk)
-
- Fill the table below for the curves given by y = 3sin(2x + 30º) and y = cos2x for x value in the range 0º ≤ x ≤ 180º (2mks)
x 0º 15º 30º 45º 60º 75º 90º 105º 120º 135º 150º 165º 180º Y = 3 sin (2x + 30) 1.50 2.60 -2.60 1.50 Y =cos 2x 1.00 0-0.87 -0.50 1.00 - Draw the graph of y = 3 sin (2x + 30º) Y = 3sin (2x + 30º) and y = cos 2x on the same axes. (4mks)
x-axis 1cm rep 15º
y-axis 1cm rep 0.5 units - Use your graph to solve the equation 3sin (2x +30º) = cos 2x (2mks)
- Determine the following from your graph
- Amplitude of y=3sin(2x+30º) (1mk)
- The period of y=3sin(2x+30º) (1mk)
- Fill the table below for the curves given by y = 3sin(2x + 30º) and y = cos2x for x value in the range 0º ≤ x ≤ 180º (2mks)
- An arithmetic progression has the first term as a and the common difference as d.
- Write down in terms of a and d the 3rd, 9th and 25th term of the progression (1mk)
- The progression is increasing, and the 3rd, 9th and 25th terms form the first three consecutive terms of a geometric series. If the sum of the 7th and twice the 6th term of arithmetic progression is 78, calculate
- The first term and the common difference of the AP. (6mks)
- The sum of the first nine terms of the AP. (3mks)
- The figure below is a right rectangular based pyramid VABCD where AB =5cm,
BC =7cm and VC =VB=VA=VD=13cm and O is a point on the base of the pyramid vertically below V.
Calculate- The length of AC (2mks)
- VO the height of the pyramid. (2mks)
- The angle between the edge VB and the plane ABCD (3mks)
- The angle between the planes VBC and ABCD (3mks)
- Three quantities L, M and N are such that L varies directly as M and inversely as the square root of N.
- Given that L = 2250 when M = 450 and N = 64, write down an equation connecting L, M and N. (4mks)
- If M decreased by 16% and N increased by 44%, calculate the percentage change in L. (3mks)
- In soccer competition, the number of goals (G) scored in a penalty shoot-out is partly constant and partly varies as the skill (S) of the player. Given that G = 8 when S = 2 and G = 12 when S =4, find the value of G when S = 6. (3mks)
- The table below shows income tax rates
A company employee earns a monthly basic salary of Ksh 28,000. He is also entitled to the following monthly allowances: house allowance of Ksh 9000, a medical allowance of sh 2000 and a commuter allowance of shs 1480.Monthly taxable pay (k£) Rate of tax ksh per £ 1- 435
436 – 870
871 – 1305
1306 – 1740
Excess over 17402
3
4
5
6- Calculate his total income tax. (5mks)
- He is entitled to a personal tax relief of Ksh 1056 per month. Determine the net tax. (1mk)
- If he received a 50% increase in his total income, calculate the corresponding percentage increase on the income tax. (4mks)

MARKING SCHEME
- x2 - 7x + 10 = 0
x2-7x = -10
x2 - 7x + 49/4 = -10 + 49/4
(x - 7/2)2 = 9/4
x - 7/2 = ± 3/2
X = 7/2 ± 3/2
Either x = 7/2 + 3/2 = 10/2 = 5
or
x = 7/2 - 3/2 = 4/2 = 2 - 75x + 50y = 70
x + y
75x + 50y = 70x +70y
5x = 20y
x/y = 20/5 = 4
x:y = 4:1 - √5 - √3 x √5 - √3
√5 + √3 √5 - √3
(√5 - √3)( √5 - √3)
5 - √15 + √15 - 3
5 - √15 - √15 + 3 = 8 - 2√15
5 - 3 2
= 4 - √15 - A = 4√d - c2g
b + c2f
A4 = d - c2g
b + c2f
A4b + A4c2f = d - c2g
A4c2f + c2g = d - A4 b
c2(A4 + g) = d - A4 b
c2 = d - A4 b
A4+ g
c = ± √d - A4 b
A4+ g - 2sm(3x+60 = 1
(3x+60) = 0.5
3x+60 = 30
3x = -30
x = -10
3x + 60 = 180 -30 = 150
3x = 150 - 60
X = 30
3x+60 = 360 +30 = 390
3x = 390 - 60 = 330
x = 110º
3x + 60 =510
3x = 450
x = 150º -
- (2 - x)8 = 28 - 27x+ 26x2 - 25x3
= 256 - 1024x + 1792x2 - 1792x2 - (1.99)8 = (2-0.01)8
= 256 - 1024 (0.01)+ 1792(0.01)2 - 1792(0.01)3
= 256- 10.24 +0:1792- 0.001792
= 245.937408
- (2 - x)8 = 28 - 27x+ 26x2 - 25x3
- 2 + log3(2x-7) = log3(5x - 7)
2log33 + log3(2x - 7) =log3(5x - 7)
log39 + log3(2x - 7) = log3(5x - 7)
log3(9(2x - 7)) = log3(5x - 7)
9(2x - 7) = 5x - 7
18x - 63 = 5x - 7
13x = 56
x = 44/3 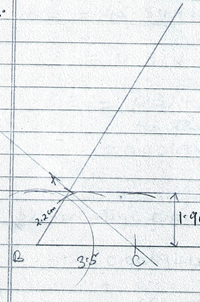
Area of ΔABC = ½ x 2.2 x 3.5sin60
3.334
ΔBCD = ½ x 3.5 x h = 3.334
h = 1.9cm
locus of Δ- x2 + y2 -6x + 84 - 11 = 0
x2 - 6x + y2 + 8y = 11
x2 4 - 6x + 9 + y2 + 8y + 16 = 11 +9+16
(x - 3)2 + (y + 4)2 = 36 = 62
(x - a)2 + (y - b)2 = r2
Centre (3, -4)
Radius - 6 units. - 8.3 ± 0.05cm by 5:45 ± 0.005 cm
- Max. Area = 8.35 x 5.455
= 45.549250 cm2
Min Area = 8.25 x 5.445
= 44.92125 cm2
Actual area = 8.3 x 5.45 = 45.235 cm2
AE = 45.54925 - 44.92125
2
= 0.314
R.E = 0.314
45.235
=0.006941527578 - Percentage error = RE x 100
= 0.006941527578 x 100
= 0.6941527578%
≈ 0.6942%(4sf)
- Max. Area = 8.35 x 5.455
- Area of Δxyz = 15.3 cm2
Area scale factor = Determinant of matrix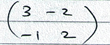 ASF = 3 x 2 - (-1x - 2)
ASF = 3 x 2 - (-1x - 2)
= 6 - 2 = 4
Area of ΔX'Y'Z = 4 x 15.3
= 61.2cm2 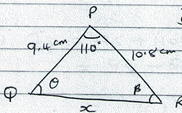 9.4 = 16:6
9.4 = 16:6
SinB Sin110
SinB = 9.4Sin110 = 0.5321
16.6
β = 32.1°
θ = 180-32.1 =147.9°
x2 = 9.42+10.82 - 2 x 9.4 x 10.8 cos110°
= 88.36 + 116.64 - 203.04 Cos110
= 88:36+ 116.64 + 203.04 x 0.3420
= 274.43968
x = 16.566cm(3d.p)- M H D
15 9 20
27 10 ?
No. of days = 15 x 20 x 9
27 x 10º
= 10 days - Tn = a + (n - 1)d
- T5 = a +(5-1) d = 71 (i)
T7 = a +(7-1) d = 59 (ii)
a + 4d = 71
a + 6d = 59
-2d = 12
d = -6
a + 4x - 6 = 71
a = 95 . - T10 = a5 + (10-1) x -6
= 95 - 54
= 41
- T5 = a +(5-1) d = 71 (i)
- 3x - 4y = 2
6x + y = 13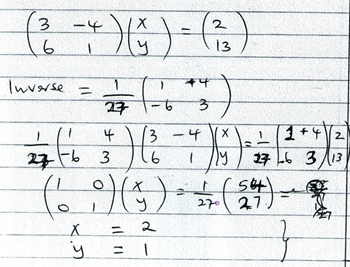
- 2x2 - x - 10
2x2 - 5x + 4x - 10
= x(2x - 5) + 2(2x - 5)
=(2x - 5)(x + 2) -
- Modal class 60-64
-
Class x f d = x - 62 d2 fd fd2 40-49 47 3 -45 225 -45 675 50-54 52 9 -10 100 -90 900 55-59 57 13 -5 25 -65 325 60-64 62 15 0 0 0 0 65-69 67 5 5 25 25 125 70-74 72 4 10 100 40 400 75-79 77 1 15 225 15 225 48≈50 ∑fd = -120 ∑fd2= 2650 - Mean
x = A + ∑fd
∑f
= 62 + -120
50
= 62 - 2.4 = 59.6 - Standard deviation
√2550 - (-120)2
50 50
= √47.24
= 6.873
- Mean
-
-
- BT = ¾BO = -¾b
- OR = 5 OA + 2 OB
2+5 2+5
= 5/7a + 2/7b - AT = AO + OT
= -a + ¼b/¼b - a
- AB = K(¼b-a) = ¼kb - ka
AD = AR + RD
= 2/7AB + h(-5/7a - 2/7b)
= 2/7(b - a) + (-5/7ha - 2/7hb)
= -2/7a - 5/7ha + 2/7b -2/7hb
= (-2/7 - 5/7h)a + (2/7 - 2/7h)b
k = -2/7 - 5/7h → k =2/7 + 5/7h
¼k = 2/7 - 2/7h
¼(2/7 + 5/7h) = 2/7 - 2/7h
h = 6/13
k = 8/13
AD = 8/13 (b-a) = 2/13b - 8/13a
-
-
-
-
- P(TB or BB)
=(2/3 x ¾) + (1/3 x 1/6)
=½ + 1/18 = 9 +1 = 10/18
18 - P(TT or BT)
=(2/3 x ¼) + (1/3 x 5/6)
= 2/12 + 5/18 = 6 +10 = 16/36
36 - P(TTB or TBB or BTB or BBB)
=(2/3 x ¼ x ¾) + (2/3 + ¼ x 1/6) + (1/3 x 5/6 x ¾) + (1/3 x 1/6 x 1/6 )
= 6/48 + 6/72 + 15/72 + 1/100
= 184/432 - 1 - 23/54 = 31/54
- P(TB or BB)
-
-
x 0º 15º 30º 45º 60º 75º 90º 105º 120º 135º 150º 165º 180º Y = 3 sin (2x + 30º) 2.60 3.00 1.50 0 -1.50 -2.60 -3.00 -1.50 0 Y =cos 2x 0.87 0.50 0 -0.50 -1.00 -0.87 0 0.50 0.87 -
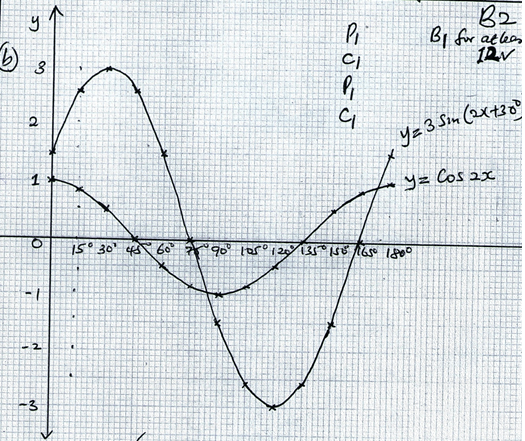
- x = 84º or 174º
-
- Amplitude 3
- Period 180º
-
- T3 = a + 2d
T25 = a + 24d -
- a +2d, a +8d, a + 24d
a + 8d = a + 24d
a + 2d a + 8d
(a + 8d)(a + 8d) = (a + 24d)(a + 2d)
a2 + 16ad + 64d2 = a2 + 26ad + 48d2
64d2 = 48d2 = 26ad - 46ad
16d2 = 10ad
10a = 16d
a = 1.6d
a + 6d + 2(a + 5d) = 78
3a + 16d = 78
4.8d + 16d = 78
20.8d = 78
d = 3.75
a = 6 - S9 = 9/2 [2 x 6 + (8 - 1)15/4]
= 9/2[12 + 30]
= 189
- a +2d, a +8d, a + 24d
- T3 = a + 2d
-
- AC = √52 + 72
= √74
= 8.602cm - VO = √132 - 4.3012
= √150.501
= 12.27 - BD = AC = 8.602
BO = ½BD = 4.301
∠VBO = θ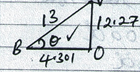
Cosθ = 4.301
13
θ = Cos-10.3308
= 70.68º - Midpoint of BC
VM = √MO2 + OV2
= √2.52 + 12.27
= √156.8029
= 12.52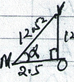
Cos x = 2.5
12.52
x = 78.48
- AC = √52 + 72
-
- L = aM
√N
2250 = 450a
√64
a = 2250 x 8 = 40
450
L = 40M
√N - M1 = 0.84M , N1 = 1.44N
L1 = 0.84aM = 0.84am
√1.44N 1.2√N
= 0.7L
%change = (0.7 - 1)L x 100%
L
= -0.3 x 100% = -30% - G = a+bs
8 = a + 2b (i)
12 = a + 4b (ii)
-4 = 2b
b = 2
a = 8 - 4 = 4
G = 4 + 2 x 6
= 4 + 12
= 16
- L = aM
-
- Total income tax
Taxable income = 28000 + 900 + 2000 + 1480
20
= 2024
Tax
435 x 2 = 870
435 x 3 = 1305
435 x 4 = 1740
435 x 5 = 2175
Rem 284 x 6 = 1704
Total income tax = 7794 - Net tax = 7794 - 1056
= 6738 - Increase in income
= 150 x 2024 = 3036
100
Total income tax = 870 + 1305 + 1740 + 2175 + 1296 x 6
= 6090 + 7776
= 13866
% increase in income tax = 13866 - 7794 x 100
7794
= 77.906%
- Total income tax
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 2 Questions and Answers - Momaliche Joint Pre Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

