Instructions to candidates
- Write your name and Admission number in the spaces provided above.
- Sign and write the date of examination in the spaces provided above.
- This paper consist of two section A and B.
- Answer all the questions in section A and B in the spaces provided.
- All working must be clearly shown.
- Mathematical tables and electronic calculators may be used.
- This paper consists of 10 printed pages.
- Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.
For examiners use only.
|
Question |
Maximum score |
Candidate’s score |
|
1-11 |
25 |
|
|
12-15 |
55 |
|
|
Total |
80 |
|

QUESTIONS
SECTION A (25 MARKS)
- The figure below shows part of a measuring cylinder containing a certain liquid.

Use this information to answer question 1 and 2
State the accuracy of the measuring cylinder (1mk) - What is the volume of the liquid in the measuring cylinder? (1mk)
- An oil drop of radius 1mm forms an oil patch of radius 1.33m on a clean water surface. If the oil spreads to make one molecule thick, estimate the size of the oil molecule. (3mks)
- The figure below shows a uniform wooden plank of length 2m and weight 5N. The plank is balanced at a distance d from one end by a mass of 1.5kg. Determine the distance d. (2mks)

- Oil is leaking from a car as it travels along a straight road. One drop falls on the ground every two seconds. The figure below shows the pattern of the drop on the ground (the figure is drawn to scale)
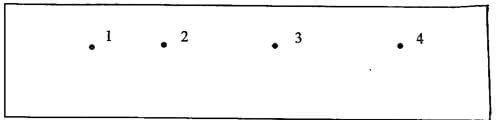
- Describe the motion of the car. (1mk)
- Determine the acceleration of the car. (2mks)
- A ball is thrown from the top of a cliff 20m high with a horizontal velocity of 10ms-1. Calculate the distance from the foot of the cliff to where the ball strikes the ground. (2mks)
- The figure below is a gas jar completely filled with water and covered with a wire gauze.
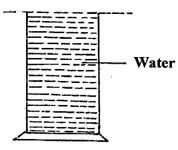
- State the observation when the set-up is suddenly invented. (1mk)
- Explain the observation made in (a) above. (2mks)
- A glass block is suspended from a spring balance and held inside a beaker without touching the beaker. Water is added gradually into the beaker. The figure below shows the variation of the upthrust on the block with depth of water in the beaker.
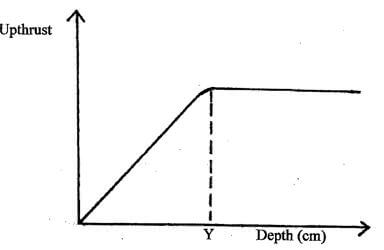
State the reasons for the observation at Y (2mks) - What force is needed to stop a 500kg car moving at 180km/h in 12.5 seconds? (3mks)
- A hole of diameter 1.0mm is made in the side of a water pipe. If the pressure of the flow is maintained at 3.0X106Nm-2, calculate the force with which the water jets out of the hole. (3mks)
- Explain why a glass container with thick glass walls is more likely to crack than one with a thin wall when a very hot liquid is poured into them. (2mks)
SECTION B (55 MARKS)
-
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N
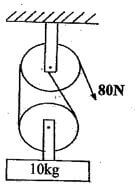
- How much potential energy does the load gain. (2mks)
- How far does the effort end move in order to raise the load by 2m? (2mks)
- How much work is done by the effort? (2mks)
- What is the efficiency of these pulleys? (2mks)
- If all the wasted energy is used to lift the bottom pulley, how much does the pulley weigh? (2mks)
- The figure below shows a wheel and axle being used to raise a load W by applying an effort E. the radius of the large wheel is R and that of small wheel is r as shown
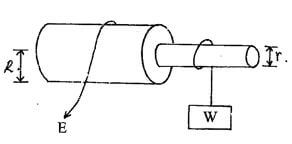
- Show that the velocity ratio (VR) of this machine is given by R/r
- Given that r=5cm and R=8cm, determine the effort required to raise a load of 20N if the efficiency of the machine is 80% (3mks)
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N
-
- A litre of gas at a temperature of 0ºC and pressure 1.0X105 Nm-2 is suddenly compressed of half its volume and its temperature rises to 273ºC. Calculate the new pressure of the gas (3mks)
- Give two differences between boiling and evaporation (2mks)
- A 1800 watts heater and a thermometer were immersed in a 1.0kg of a liquid in a copper calorimeter. Temperature was recorded after every one minute. The results obtained are in the table below.
Temperature oC
30
36
40
45
49
54
57
Time (in min)
3
4
5
6
7
8
9
- Plot a graph of temperature against time. (5mks

- Use the graph to determine.
- The room temperature (1mk)
- The specific heat capacity of the liquid take:
Specific heat capacity of copper = 400Jkg-1k-1 (4mks)
Mass of copper calorimeter = 100g
- Plot a graph of temperature against time. (5mks
-
-
- State the law of floatation (1mk)
- A balloon made up of a fabric weighing 80N has a volume of 1 x 107cm3. The balloon is filled with hydrogen of density 0.09kgm-3. Calculate the greatest weight in addition to that of the hydrogen and its fabric which the balloon can carry in air of average density 1.25kgm-3 (4mks)
- The diagram below shows the same metal block weighted in air, water and liquid X.
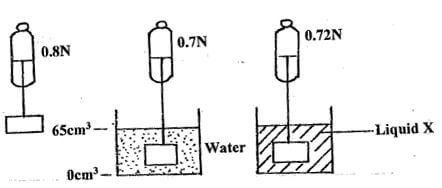
- Calculate the density of the metal. (3mks)
- Water level before the solid was immersed. (2mks)
- Density of the liquid X (3mks)
-
-
-
- Differentiate between centripetal and centrifugal forces. (1mk)
- What provides the centrifugal force needed to make a car travel round in a bend of unbanked road. (1mk)
- Below is a diagram of an aircraft of mass 2000kg together with the pilot performing some air maneuvers in a vertical plane?
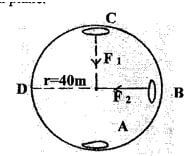
If the radius of the circular path is 40m and the aircraft is moving at a velocity of 200ms-1. Calculate- The external force F1 provided by the air at point C. (3mks)
- The external force F2 provided by the air at point B. (3mks)
-

MARKING SCHEME
SECTION A (25 MARKS)
- The figure below shows part of a measuring cylinder containing a certain liquid.

Use this information to answer question 1 and 2
State the accuracy of the measuring cylinder (1mk)
- 1cm3
- What is the volume of the liquid in the measuring cylinder? (1mk)
- 47cm3
- Volume of drop= 4/3πr3
- 4/3 x π x (0.5 x 10-3)3
- 0.5256 x 10-9m3
- An oil drop of radius 1mm forms an oil patch of radius 1.33m on a clean water surface. If the oil spreads to make one molecule thick, estimate the size of the oil molecule. (3mks)
- Volume of patch =πr2h = h=0.5256 x 10-3m3
- h= 0.5256 = 1.768g x 10-9
1.332 x π
- The figure below shows a uniform wooden plank of length 2m and weight 5N. The plank is balanced at a distance d from one end by a mass of 1.5kg. Determine the distance d. (2mks)

- 15d=(1-d)5=5-5d
- 20d=5
- d=0.25m
- Oil is leaking from a car as it travels along a straight road. One drop falls on the ground every two seconds. The figure below shows the pattern of the drop on the ground (the figure is drawn to scale)

- Describe the motion of the car. (1mk)
- The car in acceleration
- Determine the acceleration of the car. (2mks)
u= 20 = 1000m/s
0.02v= 40 =2000m/s
0.02a=2000 - 1000 = 25000m/s2
0.04
- Describe the motion of the car. (1mk)
- A ball is thrown from the top of a cliff 20m high with a horizontal velocity of 10ms-1. Calculate the distance from the foot of the cliff to where the ball strikes the ground. (2mks)
- The figure below is a gas jar completely filled with water and covered with a wire gauze.

- State the observation when the set-up is suddenly invented. (1mk)
- Water does not come out
- Explain the observation made in (a) above. (2mks)
- Atmospheric pressure supports the water by pushing the water upwards
- State the observation when the set-up is suddenly invented. (1mk)
- A glass block is suspended from a spring balance and held inside a beaker without touching the beaker. Water is added gradually into the beaker. The figure below shows the variation of the upthrust on the block with depth of water in the beaker.

State the reasons for the observation at Y (2mks)
- The block is fully immersed, no further change in up thrust
- What force is needed to stop a 500kg car moving at 180km/h in 12.5 seconds? (3mks)
- F = m(v - u)
t
500(0 - 50)
12.5
= 200N
- F = m(v - u)
- A hole of diameter 1.0mm is made in the side of a water pipe. If the pressure of the flow is maintained at 3.0X106Nm-2, calculate the force with which the water jets out of the hole. (3mks)
- A = πd2 = 3.14 x (10-3)2 = 7.85 x 10-7
4 4 - P= F/A
- F=3.0 x 106 x 3.14 x 10-6
- =2.36N
- A = πd2 = 3.14 x (10-3)2 = 7.85 x 10-7
- Explain why a glass container with thick glass walls is more likely to crack than one with a thin wall when a very hot liquid is poured into them. (2mks)
Glass is a poor conductor of heat
For thick glass inner wall gains heat and expands while the outer wall does not. The tension between the two walls break the glass
SECTION B (55 MARKS)
-
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N

- How much potential energy does the load gain. (2mks)
- P.E =mgh
- =10 x 2 x 10
- 200J
- How far does the effort end move in order to raise the load by 2m? (2mks)
- Distance moved by effort = 2 x 2 = em
- How much work is done by the effort? (2mks)
- Work done =f x d
- 10 x 4 =40J
- What is the efficiency of these pulleys? (2mks)
- M.A. x 100%
V.R. - 100 x 1/2 x 100 = 125
- 80 2
- =62.5%
- M.A. x 100%
- If all the wasted energy is used to lift the bottom pulley, how much does the pulley weigh? (2mks)
- 320 - 200 = 120
- Mg= 120/h = 120/2 = 60N
- How much potential energy does the load gain. (2mks)
- The figure below shows a wheel and axle being used to raise a load W by applying an effort E. the radius of the large wheel is R and that of small wheel is r as shown

- Show that the velocity ratio (VR) of this machine is given by R/r
V.R = distance moved by effort = 2πR = R
distance moved by the load 2πr r - Given that r=5cm and R=8cm, determine the effort required to raise a load of 20N if the efficiency of the machine is 80% (3mks)
V.R = 8/5, 80% = load/effort x 5/8 x 100
load = 20/effort
= 20/1.28 = 15.625N
- Show that the velocity ratio (VR) of this machine is given by R/r
- Using the pulley system shown a mass of 10kg is raised 2m by an effort of 80N
-
- A litre of gas at a temperature of 0ºC and pressure 1.0X105 Nm-2 is suddenly compressed of half its volume and its temperature rises to 273ºC. Calculate the new pressure of the gas (3mks)
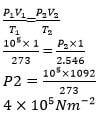
- Give two differences between boiling and evaporation (2mks)
Boiling
Evaporation
Occurs at a specific temperature
Occurs throughout the liquid
Occurs at all temperature
Occurs at the surface
- A 1800 watts heater and a thermometer were immersed in a 1.0kg of a liquid in a copper calorimeter. Temperature was recorded after every one minute. The results obtained are in the table below.
Temperature oC
30
36
40
45
49
54
57
Time (in min)
3
4
5
6
7
8
9
- Plot a graph of temperature against time. (5mks
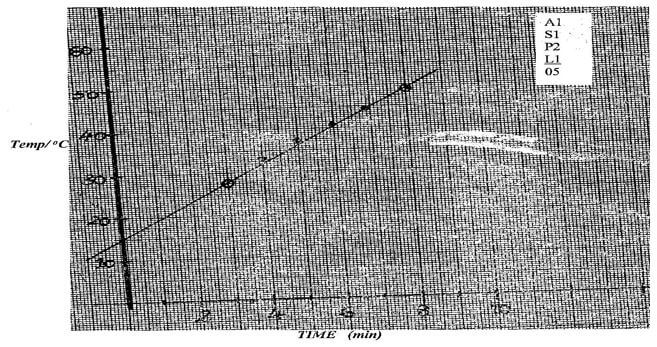
- Use the graph to determine.
- The room temperature (1mk)
- 115.5%
- The specific heat capacity of the liquid take:
Specific heat capacity of copper = 400Jkg-1k-1 (4mks)
Mass of copper calorimeter = 100g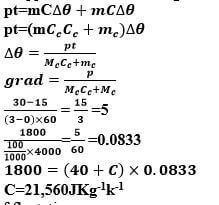
- The room temperature (1mk)
- Plot a graph of temperature against time. (5mks
- A litre of gas at a temperature of 0ºC and pressure 1.0X105 Nm-2 is suddenly compressed of half its volume and its temperature rises to 273ºC. Calculate the new pressure of the gas (3mks)
-
-
- State the law of floatation (1mk)
- Floating objects displaced their own weight of the fluid in which they float
- A balloon made up of a fabric weighing 80N has a volume of 1 x 107cm3. The balloon is filled with hydrogen of density 0.09kgm-3. Calculate the greatest weight in addition to that of the hydrogen and its fabric which the balloon can carry in air of average density 1.25kgm-3 (4mks)
- Upthurst = weight of air displaced
- =v x ℑ x g
- 107 x 10-6 x 1.25 x 10
- =125N
Weight of hydrogen = 10 x 0.09 x 10 = 9N
Total weight of Hydrogen + fabric = 9+80=89N
Total additional weight to be lifted
=125 - 89 = 36N
- State the law of floatation (1mk)
- The diagram below shows the same metal block weighted in air, water and liquid X.

- Calculate the density of the metal. (3mks)
- R. D of solid = weight of solid
upthrust in water - Up thrust = 0.8 - 0.7 = 0.1 N
- D = 0.8 = 8
0.1 - Density of solid = 8 x 1000 = 8000Kgm-3
- R. D of solid = weight of solid
- Water level before the solid was immersed. (2mks)
- Up thrust = 0.1N
- Mass of water displaced = 10g
- Volume = m/s= 10/1 = 10cm3
- Level = 65 - 10 = 55cm3
- Density of the liquid X (3mks)
- Up thrust in liquid x = 0.8 - 0.72 = 0.08N
- D = 0.08/0.1= 0.8 ℑ = 800gm-3
- Calculate the density of the metal. (3mks)
-
-
-
- Differentiate between centripetal and centrifugal forces. (1mk)
- Centripetal force is centre seeking force where as centrifugal force acts away from the centre
- What provides the centrifugal force needed to make a car travel round in a bend of unbanked road. (1mk)
- Frictional force
- Differentiate between centripetal and centrifugal forces. (1mk)
- Below is a diagram of an aircraft of mass 2000kg together with the pilot performing some air maneuvers in a vertical plane?

If the radius of the circular path is 40m and the aircraft is moving at a velocity of 200ms-1. Calculate- The external force F1 provided by the air at point C. (3mks)
- At point C, F1 +mg=mv2/r
- F1 =MV2/r- mg
- =1000 x (200)2 - 1000 x 10
40 - 1000,000 - 10000 = 990 000N
- The external force F2 provided by the air at point B. (3mks)
- F1 =MV2/r- mg
- =1000 x (200)2 - 1000 x 10
40 - 1,000,000N
- The external force F1 provided by the air at point C. (3mks)
-
Download Physics Paper 1 Questions and Answers - Asumbi Girls Highschool Pre-Mock Exams May-June 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

