Mathematics Paper 2 Questions and Answers - Mumias West Pre Mocks 2022

QUESTIONS
Answer ALL the questions in this section.

1. Use logarithms to evaluate:
   ∛45.3 × 0.00697(3 marks)
            0.534
2.      
   1. Expand (1-½x)⁶ to fourth term. (2 marks)
   2. Use the expansion above to evaluate (0.98)⁶ (2 marks)
3. The price of a new car is shs. 800,000. If it depreciates at a constant rate to shs. 550,000 within 4 years, find the annual rate of depreciation. (3 marks)
4. Object A of the area 10cm² is mapped onto its image B of area 60cm² by a transformation whose matrix is given by P = (^x₃ ⁴ _x+3). Find the positive values of x. (3 marks)
5. Without using a calculator or mathematical tables, express     √3      in surd form and simplify. (3 marks)
                                                                                                 1-Cos30º
6. Pipe A can fill a tank in 2 hours, Pipe B and C can empty the tank in 5 hours and 6 hours respectively. How long would it take:
   
   1. To fill the tank if A and B are left open and C is closed. (2 marks)
   2. To fill the tank with all pipes open. (2 marks)
7. The position vector of A and B are a = 4i + 4j – 6k and b = 10i + 4j + 12k. D is a point on AB such that AD:DB is 2:1. Find the co-ordinates of D. (2 marks)
8. Given that y is inversely proportional to xn and k is the constant of proportionality and that x=2, when y=4.5 , and x=3, when y=⁴/₃. Find the values of n and k. (4marks)
9. The coordinates of the end points of diameter are A(2,4) B(-2,6). Find the equation of a circle in the form ax2 + by² +cx + dy + e = 0 (3 marks)
10. Given that the mean of 9, 8, 5, 5 and 8 is 7; find the standard deviation of the numbers to 2 d.p (3 marks)
11. A vendor mixed grade 1 rice and grade 2 rice in the ratio 1:3 to form a mixture which she sold at sh.105 making a profit of 40%.Given that the cost price of grade 2 rice is sh.80 per kg. Find the cost price of 1kg grade 1 rice. (3marks)
12. Chord WX and YZ intersect externally at Q. The secant WQ =11cm and QX =6cm while ZQ=4cm
    
    
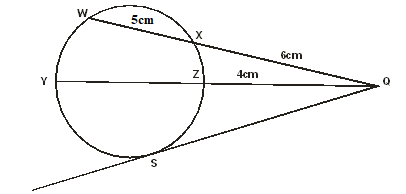
    1. Calculate the length of chord YZ (2 marks)
    2. Find the length of the tangent SQ (2 marks)
13. Given that x, y and z are integers and that 8 ≤ x ≤ 10, 5 ≤ y ≤ 7, 4≤ z ≤ 6.
    Find the percentage error in ^x+y/_z (3 marks)
14. Solve the equation below by completing the square. 5-9x-2x²=0 (2 marks)
15. Solve the simultaneous equations
    2x - y = 3
    x² –xy = -4 (3marks)
16. Solve the equation
    Log₂ (2+3x) +3log₂2 = 2 + log₂ (2x+6) (3marks)

ANSWER ANY FIVE QUESTIONS IN THIS SECTION

17. Two fair dice one a regular tetrahedron (4 faces) and the other a cube are thrown. The scores are added together.
    1. Draw a table to show all possible outcomes. (2 marks)
    2. Find the probability that:
       1. The sum is 6. (1 mark)
       2. The sum is an odd number. (1 mark)
       3. The sum is 6 or 9. (2 marks)
    3. If a player wins a game by throwing a sum of 6 or 9, draw a tree diagram and use it to find probability that he wins at least once when the dice are thrown twice. (4 marks)
18. The Hire Purchase (H.P) price of a public address system was Ksh 448 000. A deposit of Ksh 112 000 was paid followed by 24 equal monthly instalments. The cash price of the public address system was 15% less than the H.P price.
    1. Calculate :
       1. The monthly instalment. (2 marks)
       2. The cash price. (2marks)
    2. A customer decided to buy the system in cash and was allowed an 8% discount on the cash price. He took a bank loan to buy the system in cash. The bank charged compound interest on the loan at rate of 16% p.a. compounded quarterly. The loan was repaid in 2years. Calculate the amount repaid to the bank by the end of the 2 years. (3 marks)
    3. Express as a percentage of the Hire Purchase price, the difference between the amounts repaid to the bank and the Hire Purchase price. (3 marks)
19. The vertices of a rectangle ABCD are ( -1, 1) , (1, 1) ,(1, 4 )and ( -1, 4 )respectively. The vertices of its image under transformation T areA’ (1,1), B’(3,1) C’ (9, 4) and D’(7, 4)     
    1. Draw on the grid provided rectangle ABCD and its image A’B’C’D’ under the transformation T. (2 marks)
    2. Describe fully the transformation (2mks)
    3. Determine the matrix of transformation(3mks)
    4. On the grid as in (a), draw rectangle A”B”C”D”, the image of rectangle ABCD under a stretch with line y=1 invariant and stretch factor 2. State the coordinates ofA”B”C”D” (3mks)
20. An arithmetic progression of 41 terms is such that the sum of the first five terms is 560 and the sum of the last five terms is -250. Find:
    1. The first term and the common difference (5marks)
    2. The last term (2marks)
    3. The sum of the progression (3 marks)
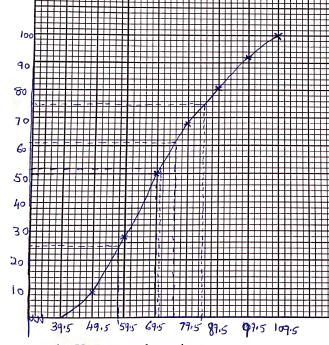
21. The table below shows the masses measured to the nearest Kg of 100 people.
    

    Mass kg	40-49	50-59	60-69	70-79	80-89	90-99	100-109
    No of people	9	19	22	18	13	11	8

    1. Draw a cumulative frequency curve for the data above. (4 marks)
    2. Use your graph to estimate
       1. The median mass. (1 mark)
       2. The number of people whose mass lies between 70.5 kg and 75.5 kg (1 mark)
    3. From your graph find
       1. The lower quartile (1 mark)
       2. the upper quartile (1 mark)
       3. the interquartile range (2 marks)
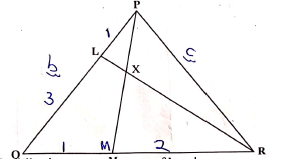
22. In the triangle PQR below L and M are points on PQ and QR respectively such that PL: LQ = 1:3 and QM: MR = 1:2, PM and RL intersect at X. Given that PQ = b and PR=c,
    
    
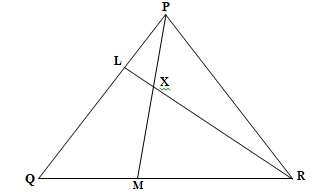
    1. Express the following vectors in terms of b and c.
       
       1. QR (1mk)
       2. PM (1mk)
       3. RL (1mk)
    2. By taking PX = hPM and RX = kRL where handk are constants find two expressions of PX in terms of h, k, b and c. Hence determine the values of the constantsh and k. (6mks)
    3. Determine the ratio LX : XR (1mk)
23. In the figure below, K L M and N are points on the circumference of a circle centre O. The points K, O, M and P are on a straight line. PQ is a tangent to the circle at N.Angle KOL = 130º and angle MKN = 40º
    
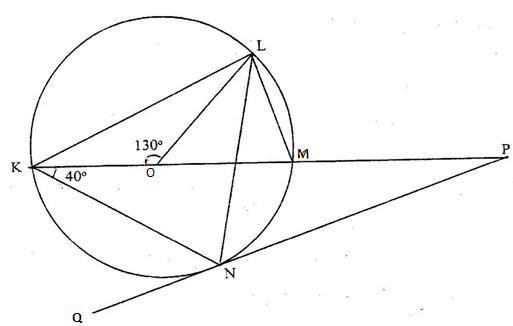
    Find the values of the following angles, stating the reasons in each case:
    1. <MLN (2mks)
    2. <OLN (2mks)
    3. < LNP (2mks)
    4. <MPQ (2mks)
    5. <KNQ (2mks)
24. Three quantities x, y and z are such that x varies directly as the square of y and inversely as the square root of z.
    1.        
       1. Given that x = 12, and y= 24, and z = 36, find x when y = 27 and z = 121 (3 marks)
       2. If y increases by 5% and z decreases by 19%,find the percentage increase in x (4 marks)
    2. If y is inversely proportional to the square root of x and that x = 4 when y = 3, calculate the value of x when y=8. (3 marks)

MARKING SCHEME

1. 
   

   No	Log
   4.53 x 101 6.97 x 10-3 5.34 x 10-1	1.6561 + 3.8432 T 4993 - T.7275 T 7718 ÷ 3

   8.392 x 10-1 T.9239
2.        
   1. 1⁶ + 6(1)5 (-x) + 15(1)4(x)² + 20(1)²(x)³
      1-3x + ¹⁵/₄ x^{2 -5}/₂x³
   2. x=0.04
      1 - 3 x 0.04 + ¹⁵/₄ x 0.042 - ⁵/₂ x 0.04³
      = 0.88584
3. 550000 = 800000 (1 - ^r/₁₀₀)⁴
   0.6875 = (1-^r/₁₀₀)⁴
   0.91058 = 
   ^r/₁₀₀ = 0.08942
   r = 8.942%
4. x(x+3) - 12 = 6
   x² + 3x -18 = 0
   x² - 3x + 6x - 18 = 0
   x(x -3) +6(x-3)=0
   (x + 6)(x - 3)=0
   x = -6 or x = 3
5. 
   
     √3   
   1-^√3/₂
     √3    x 1 +^√3/₂
   1-^√3/₂    1+^√3/₂
   √3 + 1.5
      1 - ¾
   √3 + 1.5
     1 - ¼
   4√3 + 6
6.          
   1. ½ - ¹/₅ = ³/₁₀
      1hr = ³/₁₀
      ¹⁰/₃ hrs = 3¹/₃hrs
   2. ½ - ¹/₅ - ¹/₆ = ²/₁₅
      it takes 7.5hrs
7.      
   
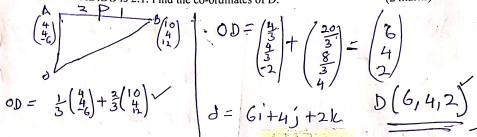
8. y = ^k/_xn
   4.5 = ^k/_2n
   4.5(2ⁿ) = k
   = ^k/_3n
   (3n) = k
   4.5(2n) = (3n)
   3.375 x 2n = 3n
   log 3.375 + nlog₂ = nlog₃
   0.52823777 = 0.17607125
   n = 3
   k = 36
   OR
   4 x 2n = 1¹/₃ x 3n
   (²/₃)n = (²/₃)³
   n = 3
   k = 36
9. Centre = (2t - 2 , 4 + 6)
                      2         2
   (0,5)
   Radius = √(2 - 0)² + (4 - 5)²
   = √4 + 1 = 5
   (x - 0)² + (y - 5)² = 5
   x² + y² - log + 25 = 5
   x² + y² - log + 20 = 0
10. 
    

    x	f	d	fd2
    9 8 5	1 2 2	2 1 -2	4 2 8 14

    SD = ¹⁴/₅ - 0
    = 1.67
11. Cost of mixture = 105 x ¹⁰⁰/₁₄₀ = sh75
    x + 80 x 3 = 75
           4
    x = 60
12.        
    1. (y + 4)4 = 11 x 6 
       4y = 66-16
       YZ = 12.5cm
    2. Q = √6 x 11
       = 8.124cm
13. Max quot. = 4.25
    Min quot. 8+5 =²¹/₆
                     6
    E = 4.25 - ²¹/₆ = 1¹/₂₄
                 2
    Actual quot. = 9+5 = 3
                             5
    ²⁵/₂₄ x 100
     3 
    = 34.7222%
14. x² + 4.5 = 2.5
    (x + 2.25)² = 2.5 + 5.0625
    x = 2.75 - 2.25 = 0.5
    or x = -5
    x = 0.5
    x = -5
15. x² - x(2 x - 3) = -4
    x² - 2x² + 3x = -4
    -x + 3x + 4 = 0
    -x + 4x - x + 4 = 0
    -x(x - 4) - 1(x - 4) = 0
    (x - 4)(-x - 1) = 0
    x = 4
    x = -1
    when x = 4
    y = 5
    when x = -1
    y = -5
16. log₂(4 + 6x) = log₂ 2(2x + 6)
    4 + 6x = 4x + 12
    2x = 8
    x = 4
17.       
    1.   
       

       	1	2	3	4	5	6
       1	2	3	4	5	6	7
       2	3	4	5	6	7	8
       3	4	5	6	7	8	9
       4	5	6	7	8	9	10

    2.      
       1. ⁴/₂₄ = ¹/₆
       2. ¹²/₂₄ = ½
       3. ⁴/₂₄ + ²/₂₄ = ⁶/₂₄= ¼
    3. 
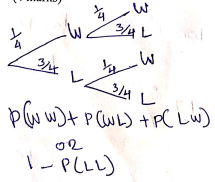       1 - ¾ x ¾ = ⁷/₁₆
18.      
    1.      
       1. 448000 - 112000 = sh14,000
                    245
       2. ⁸⁵/₁₀₀ x 448000 = sh380000
    2. CP ⁹²/₁₀₀ x 380000 = 350336
       A = 350336(1 + ¹⁶/₁₀₀)⁴
       = sh409843.5685
    3. (448000 - 409843.5685) x 100
                   448000
       = 8.517%       
19.        
    1.        
       
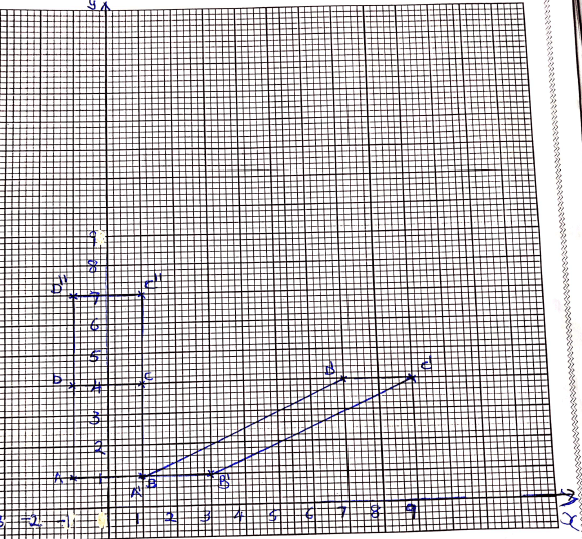
    2. It is a shear x - axis invariant
       D(-1, 4) → D1(7, 4)    
    3. (¹₀ ^k₁) (^-1₄) = (74)
       -1 + 4k = 7
       k = 2
       (¹₀ ²₁)
    4. A¹¹(-1, 1) B¹¹(1, 1) C¹¹(1, 7) D¹¹(-1, 7)
20.        
    1. 560 = 5/2(2a + 4d)
       1120 = 10a + 20d
       a + 2d = 112
       a + 40d + a + 39d + a + 38d + a + 37d + a + 36d = -250
       5a + 190d = -250
       a + 38d = -50
       a + 2d = 112
       36d = -162 
       d = -4.5
       a = 121
    2. 121 + 40 x -4.5
       = -59
    3. S₄₁ = ⁴¹/₂(121 - 59) = 1271
       OR
       ⁴¹/₂(2 x 121 + 40x - 4.5) = 1271
21. 
    

    C.F	9	28	50	68	81	92	100
    Mass kg	40-49	50-59	60-69	70-79	80-89	90-99	100-109
    No of people	9	19	22	18	13	11	8

    1.    
       
    2.       
       1. 69.5
       2. 61 - 52 = 9
    3.      
       1. 57.5
       2. 84.5
       3. 84.5 - 57.5
          = 27
22. 
             
    
    1.         
       1. -b + c
       2. ²/₃b + ¹/₃c
       3. -c + 1/3b
    2. px = h(²/₃b + ¹/₃c)
       = c + k(-c + ¹/₃b)
       c - kc + ¹/₃kb
       ²/₃hb + ¹/₃hc = c - kc + ¹/₃kb
       ¹/₃h = 1 - k 
       ¹/₃h= 1-2h
       2¹/₃h = 1
       h = ³/₇
       k = ⁶/₇
    3. 1:6
23.      
    1.    
       
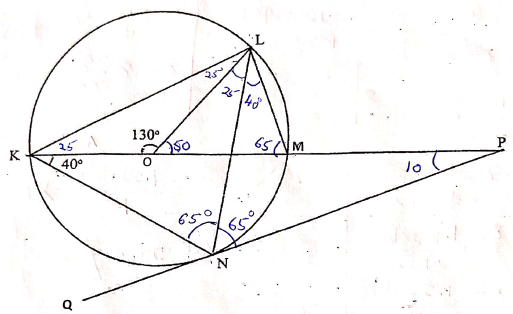
    2. 40º angles subtended by same arc MN
    3. LOM = 50º Angles on a straight line
       LMK = 65º Angles on circumfrence a chord is half that at the centre
    4. OLN = 25º
       NKL = LNP = 65º Angles in alternate segment are equal
    5. 10º sum of angles in a triangle
    6. 50º angles on a straight line add up to 180º
24.      
    1.      
       1. x = ky²
                √z
          12 = 24²k
                    6
          12 = 96k
          k = ¹/₈
          x = 0.125y²
                   √z
          x = 0.125 x 27²
                    √121
          x = 8 ²⁵/₈₈
       2. x = k(1.05y)²
                 √0.81z
          x = 1.1025ky²
                   0.9√z
          x = 1.225ky²
                   √z
          %increase = 1.225 - 1 x 100
                                   1
          = 22.5%
    2. y = ^k/_√x
       3 = ^k/₂
       k = 6
       8 = ⁶/_√x
       64 = ³⁶/_x
       x = ³⁶/₆₄
       x = 0.5625