Physics Paper 3 Questions and Answers - Mumias West Pre Mocks 2022

QUESTIONS

Question 1

• You are provided with the following:
• a voltmeter
• two new dry cells and a cell holder
• a switch
• a resistor labeled R (4Ω)
• a wire mounted on a mm scale and labeled G.
• a micrometer screw gauge (to be shared)
• six connecting wires with six crocodile clips

Proceed as follows

1.        
   1. Record the length L0 of the wire labeled G
      L0 = ……………………………………………………… (1 mk)
   2. Use the micrometer screw gauge provided to measure the diameter of the wire labeled G at two different points and determine the average diameter, d.
      The diameter d1 = ……………………mm, d2 = …………………………mm (1mk)
      Average diameter d = ………………………….. mm (1mk)
   3. Determine the radius r of the wire in metres.
      Radius r = ………………………………………………. m (1mk)
2. Set up the apparatus as shown in the circuit diagram in the figure below.
   
   
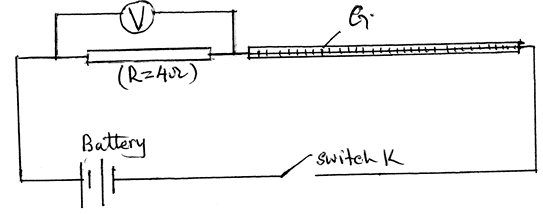
   1. Use the voltmeter provided to measure the p.d VR across R and the p.d, VG across G when the switch is closed.
      VR = ……………………………………………. Volts (1/2 mk)
      VG = ……………………………………………. Volts (1/2 mk)
      Open the switch
   2. Use the value of R provided and the value of VR in b (i) above to determine the current I flowing through R when the switch was closed.
      I = ………………………………………………….Amperes (1mk)
   3. Determine the constant H given that
      H = 100V_G
              I  xL₀
      H = ………………………………………………… Ωm-1 (1mk)
3. Connect the voltmeter across R as shown in the figure below.
   
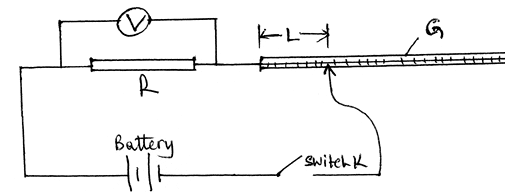
   Adjust the position of one crocodile clip on the wire G to a point such that the length L of the wire in the circuit is 5cm (see the figure above). Close the switch.
   Read and record in the table 2 the value for the p.d across R. Open the switch.
4. Repeat the procedure in (c) above for the other values of L shown in table 2. (3mks)
   Table 2
   

   Distance L (cm)	0	5	10	20	30	40	60	70
   p.d V across R (V)

5.      
   1. On the grid provided plot the graph of V (y-axis) against L (5mks)
      
   2. From the graph determine L1, the value of L when V = V0/2 where V0 is the p.d when L = 0 (1mk)
6. Determine the constant D for the wire given that (2mks)
   D = R  X 300
         L1     V0
7. Determine the constant p given that
   p = πr ² (D + H) where r is the radius of the wire in metres. (2 mks)
         2

Question 2

You are provided with the following apparatus:

• clamp
• boss
• stand
• optical pin
• copper wire (15 cm long)
• protractor
• two pieces of plasticine of about 0.5cm diameter
• cork

1. Set up the apparatus as shown in the diagram below
   
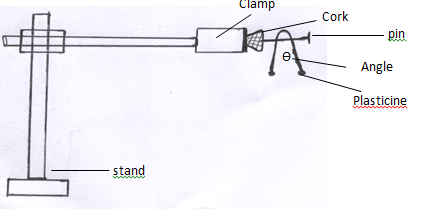
2. Bend the wire in the middle so as to make an angle of 500. Attach the two small pieces of plasticine at both ends of the bent wire as shown in the diagram.
3. Place the bent wire on the optical pin and give a small horizontal displacement. Take the time for 10 complete oscillations and record in the table below.
4. Repeat the procedure above for other values of and complete the table below. (9mks)
   

   Angle θº	Time’t’ for 10 oscillations(s)	Period T (s)	Frequency f (Hz)	f2(Hz)2	Cos(θ/2)
   50
   60
   70
   80
   90
   100

   1. On the graph paper provided, pot a graph of f² (y-axis) against Cos^θ/₂ (5mks)
      
      Determine the gradient ‘S’ of the graph (3 mks)
   2. The equation for the oscillation of the wire is given by the formula:
      f2 = 150 Z Cos(^θ/₂)
            4π²L
      Given that L = 0.15m, use the gradient of the graph to determine the value of Z. (3mks)

CONFIDENTIAL

QUESTIONS

Question 1

• A nichrome wire (S.W.G.  30, 0.28mm diameter and length 80cm) free of kinks labelled G and mounted on a mm scale
• A Switch
• Voltmeter (0- 3V) or (0-5V) scale
• 2 new dry cells in a cell holder
• A resistor labeled R (4Ω)
• A micrometer screw gauge (to be shared)
• Six connecting wires with six crocodile clips

Question 2
You are provided with the following apparatus:

• clamp
• boss
• stand
• optical pin
• copper wire (15 cm long)
• protractor
• two pieces of plasticine of about 0.5cm diameter
• cork

MARKING SCHEME

1.      
   1.      
      1. 80.0 cm
      2. d1 = 0.30 ± 0.02 
         d2 = 0.30 ± 0.0.2
         d = 0.30 + 0.30 = 0.30
                 2
      3. 0.30 = 0.15 = 0.0015m
           2      100
   2.      
      1. 1.70
         1.30
      2. I = V/R = 1.7/10 = 0.17
      3. 100 x 1.03 = 955.88
         0.17 x 0.80
   3.        
   4.        
      Table 2
      

      Distance L (cm)	0	5	10	20	30	40	60	70
      p.d V across R (V)	2.55	2.20	2.00	1.90	1.70	1.65	1.45	1.30

   5.      
      1.      
         
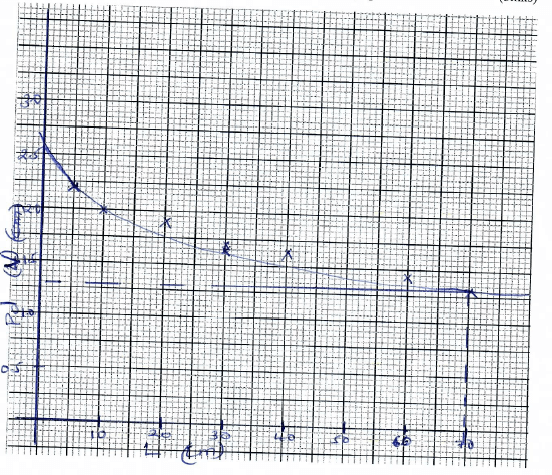
      2. V0/2 = ^2.60/₂ = 1.3
         L = 70cm
   6. D = 10 x 300
      70cm 2.6V
      = 3000v²
         70x26
      16.48 R/cm.v
      or 1648 R/mv
   7. P = ²²/₇ x 0.0015² (1648 + 955.88)
                          2
      = 9.2066 x 10^-3
2.      
   

   Angle θº	Time’t’ for 10 oscillations(s)	Period T (s)	Frequency f (Hz)	f2(Hz)2	Cos(θ/2)
   50	5.53	0.553	1.8083	3.2700	0.9063
   60	5.90	0.590	1.6949	2.8727	0.8660
   70	6.06	0.606	1.6502	2.723	0.8192
   80	6.63	0.663	1.5083	2.2750	0.7660
   90	7.31	0.735	1.3680	1.8714	0.7071
   100	7.65	0.765	1.3072	1.7085	0.6423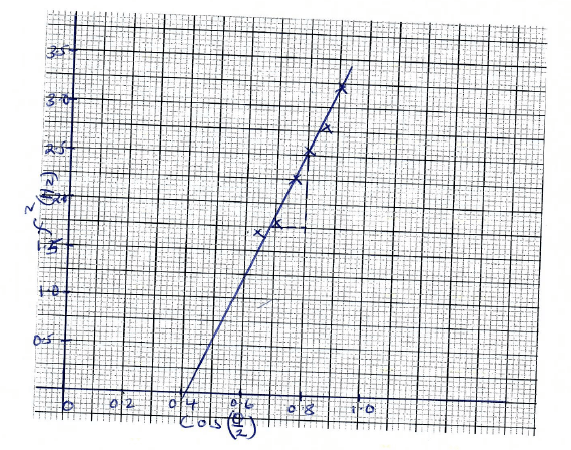

   1. 
      
      S =    Δt  ²
            cos(^θ/₂)
      = 2.5 - 1.75 = 0.75 = 6.25Hz
        0.8 - 0.68     0.12
   2.      150      Z = 6.25
      4π² x 0.15
      Z = 6.25 x 4π² x 0.15
                      150
      = 0.2467