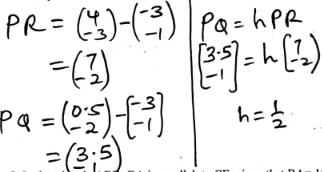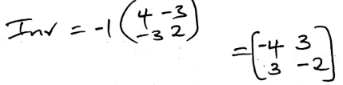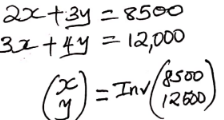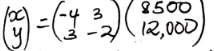Mathematics Paper 1 Questions and Answers - Kassu Jet Pre Mocks 2022

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Kassu Jet Pre Mocks 2022

Download PDF for future reference Get on Whatsapp for 50/-

Instructions to candidates

The paper contains TWO sections: Section I and Section II.
Answer ALL the questions in Section I and any five questions from Section II
Show all the steps in your calculations, giving your answers at each stage
Marks may be given for correct working even if the answer is wrong.
Non – programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I (50 MARKS)
Answer all questions in this section on the spaces provided

An aircraft Company bought eight aircrafts for eighteen billion, nine hundred and seventy-five million, twenty-eight thousand, two hundred and forty.
1. Write the total cost of the eight aircrafts in figures. (1mark)
2. Calculate the cost of each aircraft. (2marks)
Solve for x in the equation 3 + 2 = 1 (4mks)
x+1 x+5 x−2
1. The number 16200 is given as 2^x × 3^y × 5^z. Find the value of x+y+z (1mark)
2. When another number N is multiplied by 16200, a perfect cube is obtained. Find the least value of N (2marks)
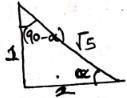
Given that sin α° = 1 where a is an acute angle find, without using Mathematical tables
√5
1. Cos α° in the form of ab, where a and b are rational numbers (2marks)
2. Tan (90 − α)° 2marks
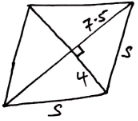
The area of a rhombus is 60 cm². If the shorter diagonal is 8 cm. Find the perimeter of the rhombus. (4 marks)
A 63kg metal of density 7,000 kg/m³ is moulded into a rectangular pipe with external dimensions of 12cm by 15cm and internal dimensions of 10cm by 12cm. Calculate the length of the pipe in meters.(3marks)
The position vectors of the points P, Q and R are (−3 −1) ,(½ −2) and (4 −3) respectively. Show that P, Q and R are collinear (3marks)
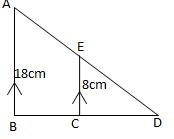
In the triangle ABD, BA is parallel, to CE, given that BA= 18cm, CE = 8cm and AE = 6cm,find the length of DE (3marks)
Given the equation 9⁴ˣ = 1 , solve for x to its simplest form. (3 marks)
3^2x 9⁻⁴
A Kenyan company received M US Dollars. The money was converted into Kenyan shillings in a bank which buys and sells foreign currencies.
Buying (in Ksh.) Selling (in Ksh.)
1Sterling Pound 145.78 146.64
US Dollar 110.66 110.86
If the company received Ksh. 15,132, 000, calculate the amount M, received in US Dollars. (2marks)
Two interior angles of an irregular n sided polygon is 117 each. The remaining exterior angles are 39° each. Calculate the number of sides of the polygon (3marks)
Determine the inequalities that represent and satisfies the unshaded region (3marks)
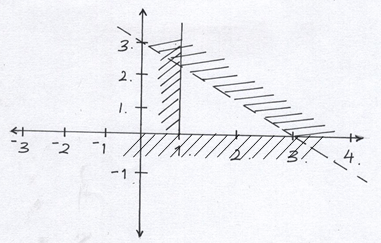
There are two grades of rice, grade A and Grade B. Grade A costs Sh 80 per Kg while Grade B costs Sh 60 per Kg. In what ratio must the two be mixed in order to produce a blend costing Sh 75 per Kg. (3marks)
One of the three vertices of triangle ABC is A (2,−3). Point A is mapped onto A^I (−4, 7) under a reflection on mirror line M. find the equation of the mirror-line M (3marks)
A camp has enough food ration to last 10,000 refugees for 35 days. After 5 days, 2500 more refugees arrived in the camp. If all are now put on a half ration, how much longer will the food last? (3 marks)

SECTION II (50 marks)
Answer any five questions from this section on the spaces provided.

1. A particle moving at 20 m/s accelerates to 30 m/s in 5 seconds then travels at this speed for 10 seconds before decelerating to rest in 4 seconds. Draw a velocity - time graph and use it to calculate the distance covered by the particle in 19 seconds. (3 marks)
2. 1. A train 100 m long travelling at 72km/h overtakes another train travelling in the same same direction at 56km/hr and passes it completely in 54 seconds. Find the length of the second train. (4 marks)
  2. Find the time (how long) they would have taken to pass each other if they had been travelling at these speeds in opposite directions. (3 marks)
1. Find the inverse of the matrix A , given that A is (2 3 3 4 )
2. Jane bought 200 bags of sugar and 300 bags of rice for a total cost of shs. 850,000. Peter bought 120 bags of rice and 90 bags of sugar for a total cost of shs. 360,000. If the price of a bag of sugar is shs. x and that of rice is shs. y.
  1. Form two equations to represent the above information. (2marks)
  2. Use matrix method to find the price of one bag of each item (3marks)
3. Robert bought 225 bags of sugar and 360 bags of rice. He was given a total discount of shs. 33,300. If the discount on the price of a bag of rice was 2%, calculate the percentage discount on the price of a bag of sugar. (3marks)
The table below shows scores for a form 4 class Math results in Ushindi School.

Marks 20-29 30-49 50-54 55-69 70-79 80-84 85-99

No. of students 3 12 6 15 5 7 3

fd
1. Fill in the column for frequency density row on the table (2marks)
2. Draw a histogram to represent the above data (3marks)
3. By using the histogram drawn above calculate the median of the data and indicate using a line where it lies in the histogram. (5marks)
1. Complete the table below for the equation y = 4x³ − 3x² − 6x 2marks
  
  x −1¼ −1 −½ 0 ½ 1 1½ 1¾
  
  y −5 1¾ −3¼ −2¼
2. Using a scale of 4 cm to represent 1 unit on the x axis and 2cm to represent 1 unit on the y-axis draw the graph of
  y = 4x³ − 3x² − 6x for −1¼ ≤ x ≤ 1¾ on the grid provided 3marks
3. Use your graph to find the range of values of x for which y ≤ −3 (1mark)
4. Use your graph to solve the equation 4x³ − 3x² − 6x = 0 (2marks)
5. By drawing a suitable straight-line graph on the same axes solve the equation (2marks)
  − 4x³ + 3x² + 7x − 1 = 0
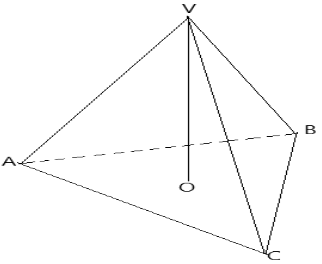
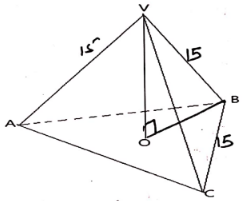
The figure below shows a solid regular tetrahedron of side 15 cm. Point O is center of the base ABC
1. Calculate the perpendicular height VO of the pyramid to 1 decimal place. (3 marks)
2. The tetrahedron is cut parallel to the base ABC forming a frustrum. The slant height of the frustrum is two-thirds the slant height of the pyramid. Calculate;
  1. The volume of the frustrum. (4 marks)
  2. The surface area of the solid frustrum (3 marks)
1. Draw the quadrilateral with vertices at A(−6,−1) B(−6,−4) C(3,−4) and D(3,−1) (1mark)
2. On the same grid, draw the image of ABCD under enlargement centre (0,−1) scale factor ¹/₃, label the image A’B’C’D’. (2marks)
3. Draw A’’B’’C’’D’’ the image of A’B’C’D’ under rotation of +90° about (1,0). (2marks)
4. Draw A’’’B’’’C’’’D’’’ the image of A’’B’’C’’D’’ under reflection in the line y − x = 0 2marks
5. Draw A^IVB^IVC^IVD^IV the image of A’’’B’’’C’’’D’’’ under translation (−2 3) and write down its coordinates (3marks)
1. The equation of a line L₁ is 7y − 5x − 20=0⋅ Find the x-intercept of the equation (1mark)
2. Another line L₂ is perpendicular to L₁ and passes through (−5, 3). Find the equation of L₂. (3marks)
3. L₃ passes through (0,−3) and parallel to the line L₄ whose equation is 3y − 8x = 3 find the equation of L₃. (3marks)
4. Calculate the coordinates of point of intersection between the lines L₁ and L₃. (3marks)
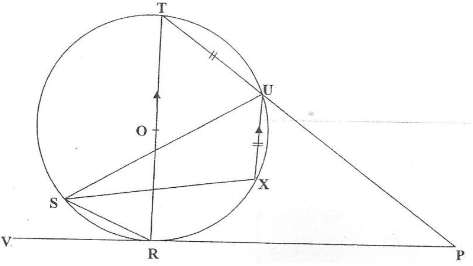
In the figure below, O is the center of the circle TOR is the diameter and PRV is tangent to the circle at R.

Given that <SUR = 25°, <URP = 60°, TU = UX and that UX is parallel to the diameter; giving reasons calculate;
1. <TOU (2 marks)
2. <XUP (2 marks)
3. <STR (2 marks)
4. Reflex <SXU (2 marks)
5. <RPU (2marks)

MARKING SCHEME

SECTION I (50 MARKS)

Answer all questions in this section on the spaces provided

An aircraft Company bought eight aircrafts for eighteen billion, nine hundred and seventy-five million, twenty-eight thousand, two hundred and forty.
1. Write the total cost of the eight aircrafts in figures. (1mark)
  18,975,028,240
2. Calculate the cost of each aircraft. (2marks)
  18,975,028,240 = 2,371,878
  8
Solve for x in the equation 3 +   2   = 1 (4mks)
x+1 x+5 x−2
3x + 15 + 2x + 2 = 1
(x+1) (x+5) x−2
(x−2)(5x+17) = (x+1)(x+5)
5x² + 17x − 10x + 34 = x² + 6x + 5
4x² + x − 39 = 0
−1±√(1+16×39)
8
= 3 or −3.25
1. The number 16200 is given as 2^x × 3^y × 5^z. Find the value of x+y+z (1mark)
  16200 = 2³ × 3⁴ × 5²
  x = 3
  y = 4
  z = 2
  3 + 4 + 2 = 9
2. When another number N is multiplied by 16200, a perfect cube is obtained. Find the least value of N (2marks)
  2³ × 3⁴ × 5²
  2⁰ × 3² × 5¹ = 45
Given that sin α° = 1 where a is an acute angle find, without using Mathematical tables
√5
1. Cos α° in the form of ab, where a and b are rational numbers (2marks)
  
  cos α = ²/_√5
  = 2√5
  5
2. Tan (90 − α)° 2marks
  Tan (90 − α) = ²/₁
  = 2
The area of a rhombus is 60 cm². If the shorter diagonal is 8 cm. Find the perimeter of the rhombus. (4 marks)

A = ½D×d
60 = ½ × 8 × D
¹²⁰/₈ = D
D = 15cm
7.5² + 4² = S²
72.25 = S²
S = 8.5cm
P = 45
= 4 × 8.5
= 34cm
A 63kg metal of density 7,000 kg/m³ is moulded into a rectangular pipe with external dimensions of 12cm by 15cm and internal dimensions of 10cm by 12cm. Calculate the length of the pipe in meters.(3marks)
V = ^m/_d
= 63
7000
=9000cm³
A_CSA = (12×15) − (10×12)
= 180 − 120
= 60cm²
V = A_CSA × L
60 × L = 9000
60 60
L = 150cm
= 1.5m
The position vectors of the points P, Q and R are (−3 −1) ,(½ −2) and (4 −3) respectively. Show that P, Q and R are collinear (3marks)

PQ = ½PR and P is common pt Hence Collinear
In the triangle ABD, BA is parallel, to CE, given that BA= 18cm, CE = 8cm and AE = 6cm,find the length of DE (3marks)

Let DE be x
¹⁸/₈ = 6 + x
x
18x = 48 + 8x
10x = 48
x = 4.8cm
Given the equation 9⁴ˣ = 1 , solve for x to its simplest form. (3 marks)
3^2x 9⁻⁴
(3²)^4x ÷ 3^2x = 1 ÷ (3²)⁻⁴
3^8x−2x = 3⁰⁻⁽⁻⁸⁾
6x = 8
x = ⁴/₃
x = 1¹/₃
A Kenyan company received M US Dollars. The money was converted into Kenyan shillings in a bank which buys and sells foreign currencies.
Buying (in Ksh.) Selling (in Ksh.)
1Sterling Pound 145.78 146.64
US Dollar 110.66 110.86
If the company received Ksh. 15,132, 000, calculate the amount M, received in US Dollars. (2marks)
15,132,000 = 136,743.1773 US$
110.66
Two interior angles of an irregular n sided polygon is 117 each. The remaining exterior angles are 39° each. Calculate the number of sides of the polygon (3marks)
180 − 117 = 63°
63 × 2 = 126°
126 + 39(n−2) = 360
39 (n−2) = 234
39 39
n − 2 = 6
n = 8 sides
Determine the inequalities that represent and satisfies the unshaded region (3marks)

x ≥ 1
y ≥ 0
y+x < 3
There are two grades of rice, grade A and Grade B. Grade A costs Sh 80 per Kg while Grade B costs Sh 60 per Kg. In what ratio must the two be mixed in order to produce a blend costing Sh 75 per Kg. (3marks)
80A+ 60B = 75
A + B
80A − 75A = 75B − 60B
5A = 15B
^A/_B = ¹⁵/₅ = ³/₁
A:B =3:1
One of the three vertices of triangle ABC is A (2,−3). Point A is mapped onto A^I (−4, 7) under a reflection on mirror line M. find the equation of the mirror-line M (3marks)
Midpoint; (2−4 , −3+7)
2 2
= (−1,2)
M1 = 7 + 3 = 10
−4−2 −6
M2 = ³/₅
y = mx + c
−3 = ³/₅(2) + c
−3 − ⁶/₅ = c = −²¹/₅
5y − 3x + 21 = 0
y = ³/₅x − ²¹/₅
A camp has enough food ration to last 10,000 refugees for 35 days. After 5 days, 2500 more refugees arrived in the camp. If all are now put on a half ration, how much longer will the food last? (3 marks)
1 Day = 10000
35
5 days = 10000 × 5
35
= 10000
7
Remainder = 8571³/₇
After new 2500 refugees
1 day = 12500 = 12500
35÷½ 70
12500x = 8571³/₇ 70
x = 48
48 − 35 = 13days

SECTION II (50 marks)
Answer any five questions from this section on the spaces provided.

1. A particle moving at 20 m/s accelerates to 30 m/s in 5 seconds then travels at this speed for 10 seconds before decelerating to rest in 4 seconds. Draw a velocity - time graph and use it to calculate the distance covered by the particle in 19 seconds. (3 marks)
  
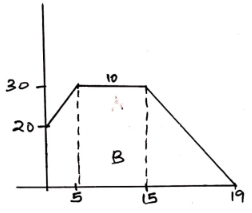
  A = (½ × 4 × 30) + ½(30+20)5 + 10×30
  = 60 + 125 + 300
  = 485m
  Area = Distance 40m
2. 1. A train 100 m long travelling at 72km/h overtakes another train travelling in the same same direction at 56km/hr and passes it completely in 54 seconds. Find the length of the second train. (4 marks)
    RS = 72 − 56
    = 16km/h
    T = 545
    D = S × T
    = 16 × ⁵/₁₈ × 54
    = 16 × 5 × 3 = 240m
    T₁ = 100m
    T₂ = 240 − 100
    = 140m
  2. Find the time (how long) they would have taken to pass each other if they had been travelling at these speeds in opposite directions. (3 marks)
    RS = 56 + 72
    = 128km/h
    D = 240m
    t = ^D/_RS
    = 240 × 1/1000
    128
    = 6.75 seconds
1. Find the inverse of the matrix A , given that A is (2 3 3 4 )
  Det = 8 − 9 = −1
2. Jane bought 200 bags of sugar and 300 bags of rice for a total cost of shs. 850,000. Peter bought 120 bags of rice and 90 bags of sugar for a total cost of shs. 360,000. If the price of a bag of sugar is shs. x and that of rice is shs. y.
  1. Form two equations to represent the above information. (2marks)
    3x + 4y = 12000
    2x + 3y = 8500
  2. Use matrix method to find the price of one bag of each item (3marks)
    
    x = −4(8500) + 3(12000)
    y = −3(8500 − 2(12000)
    x = 2000
    y = 1500
3. Robert bought 225 bags of sugar and 360 bags of rice. He was given a total discount of shs. 33,300. If the discount on the price of a bag of rice was 2%, calculate the percentage discount on the price of a bag of sugar. (3marks)
  33,300 − (0.02 of 360 × 1500)
  = 22,500
  22500 × 100
  225×2000
  = 0.05 × 100
  = 5%

The table below shows scores for a form 4 class Math results in Ushindi School.

	3	15	21	36	41	48	51
Marks	20-29	30-49	50-54	55-69	70-79	80-84	85-99
No. of students	3	12	6	15	5	7	3
fd	0.3	0.6	1.2	1	0.5	1.4	0.2

Fill in the column for frequency density row on the table (2marks)
Draw a histogram to represent the above data (3marks)
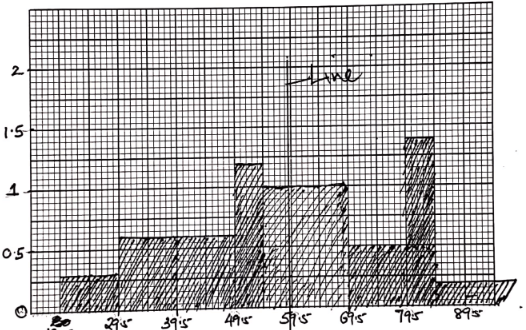
By using the histogram drawn above calculate the median of the data and indicate using a line where it lies in the histogram. (5marks)
⁵¹/₂ = 25.5
Median class = 55 – 69
54.5 + (25.5 − 21)15
15
54.5 + 4.5 = 59

1. Complete the table below for the equation y = 4x³ − 3x² − 6x 2marks
  
  x −1¼ −1 −½ 0 ½ 1 1½ 1¾
  
  y −5 −1 1¾ 0 −3¼ −5 −2¼ 1¾
2. Using a scale of 4 cm to represent 1 unit on the x axis and 2cm to represent 1 unit on the y-axis draw the graph of
  y = 4x³ − 3x² − 6x for −1¼ ≤ x ≤ 1¾ on the grid provided 3marks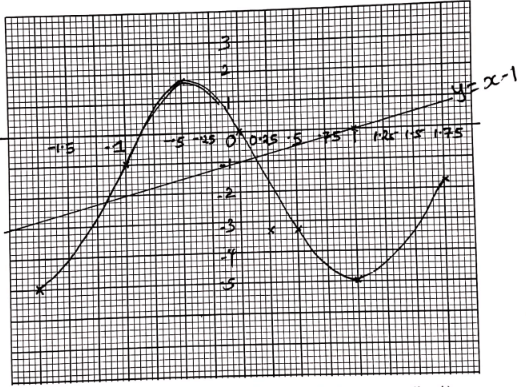
3. Use your graph to find the range of values of x for which y ≤ −3 (1mark)
  0.45 to 1.55 and −1.3 to −1.75
4. Use your graph to solve the equation 4x³ − 3x² − 6x = 0 (2marks)
  0 and −0.85
5. By drawing a suitable straight-line graph on the same axes solve the equation (2marks)
  − 4x³ + 3x² + 7x − 1 = 0
  − 4x³ + 3x² + 7x − 1 = 0
  − 4x³ + 3x² + 7x + 0 = y +
  y = −1 + x
  y = x − 1
  x = 0.175 and 1.175
The figure below shows a solid regular tetrahedron of side 15 cm. Point O is center of the base ABC
1. Calculate the perpendicular height VO of the pyramid to 1 decimal place. (3 marks)
  
  ²/₃(√15² − 7.5²) = BO
  = 8.66
  15² − 8.66²
  √(225 – 75) = VO
  = 12.2cm
2. The tetrahedron is cut parallel to the base ABC forming a frustrum. The slant height of the frustrum is two-thirds the slant height of the pyramid. Calculate;
  1. The volume of the frustrum. (4 marks)
    V_T = ¹/₃ × ½ × 15² sin 60 × 12.2
    = 396.206
    V_SF = 27:1
    V_ST = ¹/₂₇ × 396.206
    = 14.67
    V_F = 396.206 − 14.67
    = 381.53
    Acc. 383.016
  2. The surface area of the solid frustrum (3 marks)
    
    [½(5+15)8.660]3
    259.81 + ½ × 15² sin 60 + ½ × 5² sin 60
    = 368.1cm²
1. Draw the quadrilateral with vertices at A(−6,−1) B(−6,−4) C(3,−4) and D(3,−1) (1mark)
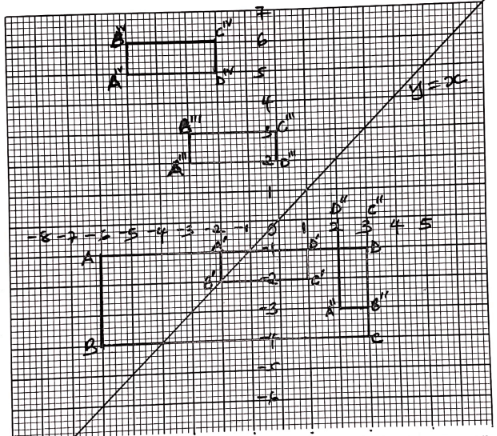
2. On the same grid, draw the image of ABCD under enlargement centre (0,−1) scale factor ¹/₃, label the image A’B’C’D’. (2marks)
3. Draw A’’B’’C’’D’’ the image of A’B’C’D’ under rotation of +90° about (1,0). (2marks)
4. Draw A’’’B’’’C’’’D’’’ the image of A’’B’’C’’D’’ under reflection in the line y − x = 0 2marks
5. Draw A^IVB^IVC^IVD^IV the image of A’’’B’’’C’’’D’’’ under translation (−2 3) and write down its coordinates (3marks)
  A^IV (−5, 5)
  B^IV (−5, 6)
  C^IV (−2, 6)
  D^IV (−2, 5)
1. The equation of a line L₁ is 7y − 5x − 20=0⋅ Find the x-intercept of the equation (1mark)
  −5x = 20
  x = − 4
2. Another line L₂ is perpendicular to L₁ and passes through (−5, 3). Find the equation of L₂. (3marks)
  M₁ = ⁵/₇
  M₂ = −⁷/₅(−5, 3)
  3 = −⁷/₅(−5) + C
  −4 = C
  y = −⁷/₅x − 4
3. L₃ passes through (0,−3) and parallel to the line L₄ whose equation is 3y − 8x = 3 find the equation of L₃. (3marks)
  M₁ = ⁸/₃
  M₂ = ⁸/₃(0,−3)
  −3 = ⁸/₃(0) + C
  −3 = C
  y = ⁸/₃x − 3
4. Calculate the coordinates of point of intersection between the lines L₁ and L₃. (3marks)
  3y − 8x = − 9
  7y − 5x = 20
  21y − 56x = −63
  −21y −15x = 60
  −41x = −123
  x = 3
  3y − 8(3) = −9
  3y = −9 + 24
  y = 5
  (3, 5)
In the figure below, O is the center of the circle TOR is the diameter and PRV is tangent to the circle at R.

Given that <SUR = 25°, <URP = 60°, TU = UX and that UX is parallel to the diameter; giving reasons calculate;
1. <TOU (2 marks)
  60° - Sum of interior angles add to 180°
2. <XUP (2 marks)
  60° - Vertically opposite angles are equal
3. <STR (2 marks)
  25° - Same chord subtends equal angles at the circumference.
4. Reflex <SXU (2 marks)
  95° - Opposite interior angles of a cyclic quadrilateral are equal
5. <RPU (2marks)
  30° - Angles of a triangle add to 180°