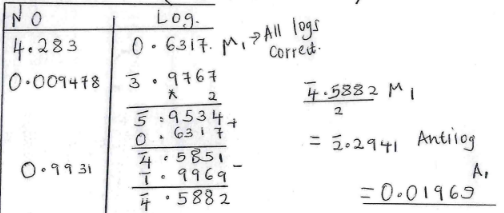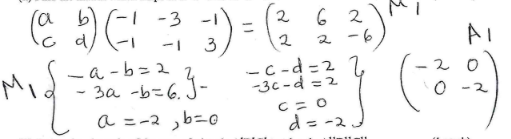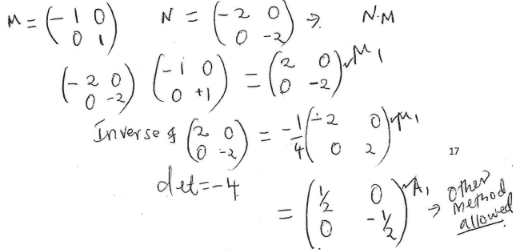- This paper consists of two sections: Section I and Section II.
- Answer ALL questions in section 1 and ONLY FIVE questions from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
SECTION I. Answer all the questions ( 50 marks)
- A student spends 3/8 of his time playing basketball, ¼ of the remaining in playing table tennis and ¾ of the remaining time playing volleyball. The rest is spent on reading novels. What fraction of the time is spent on reading novels?
(3 marks) - Simplify; √5 − 1 (3 marks)
√5 + 1 - Solve the equation 2 log 3 + log (x−2) = 2 log x (3 marks)
- The base and perpendicular height of a triangle measured to the nearest millimetre are 15.0 cm and 9.5 cm respectively. Find:
- The absolute error in calculating the area of the triangle (1 mark)
- The percentage error in the area, giving the answer to 1 decimal place. (3 marks)
- Find the value of θ, given that; ½ sin = 0.35 for 0° ≤ θ ≤ 360° (3 marks)
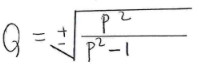
- Make Q the subject of formula P =
(3 marks)
- The coordinates of the end points of a diameter of a circle are A2,4 and B(2,6). Find the equation of the circle in the form ax2 + by2 +cx + dy + e = 0 (4 marks)
- Kimani wants to buy a TV on hire purchase. It has a cash price of Ksh.30,000. He makes a down payment of Ksh.9,000 and 12 monthly instalments of ksh. 2,200 each. Calculate the rate of compound interest charged per month.(Give your answer to 1 dp). (3 marks)
- Expand (3 + 3x)6 in ascending powers of x. Hence use the expansion up to the 3rd term, to find the value of (3.03)6 correct to 2 decimal places. (3 marks)
- The following are ages of students in a class 7,9,8,9,11,12,10 9,8,6,7,10,11,12,6,9,7, and 11.
- Complete the frequency distribution table below (1 mark)
Ages 6 7 8 9 10 11 12 No of students - Calculate the standard deviation of their ages in five years’ time. (2 marks)
- Complete the frequency distribution table below (1 mark)
- Find the possible values of x given that
is a singular matrix. (3 marks)
- Evaluate using the logarithm table; (4 marks)
( log 9.814 )−½
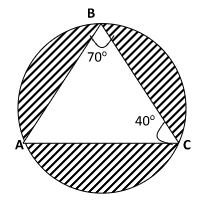
[4.283 × (0.0094782)²] - The figure below is that of a circumcircle of the triangle ∠ABC. The radius of the circle is 5cm. Given that ∠ABC = 70° and ΔACB=40°. Calculate the area of ABC . (3 marks)
- A quantity P varies partly as the cube of Q and partly varies inversely as the square of Q. when Q = 2, P = 108 and when Q = 3, P = 259. Find the value of P when Q = 6. (3 marks)
- The table below shows the number of insects and corresponding number of days in breeding.
Number of insects 200 300 400 500 600 700 800 900 Days 4.4 6.4 7.4 8.0 8.5 9.0 9.5 10 - On the grid provided, draw the graph of number of insects against the number of days. (1 mark)
- Determine the rate of breeding between 5th and 7th day. (2 marks)
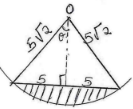
- Calculate the area of the minor segment of a circle of radius 5√2cm, cut off by a chord of length 10cm. (3 marks)
SECTION II: Answer any 5 questions from this section. ( 50 marks)
- Income rates for income earned were charged as shown in the table alongside:
A civil servant earns a monthly salary of Ksh.27,000. He was also given a house allowance of Ksh. 12,000 , transport allowance Ksh.1,800 and medical allowance Ksh.2,000. He is entitled to a family relief of Kshs. 1040 per month.
Determine:Income in Ksh. pm Rate in Ksh. Per Shs. 20 1- 8400 2 8401- 18,000 3 18,001- 30,000 4 30,000 - 36,000 5 36,000-48,000 6 48,001 and above 7 -
- His taxable income per month in Ksh. (2 marks)
- His net tax. (6 marks)
- In addition, the following deductions were made
NHIF Ksh. 430
Loan repayment Ksh. 6500
Bank shares Ksh. 1000.
Calculate his net pay per month. (2 marks)
-
-
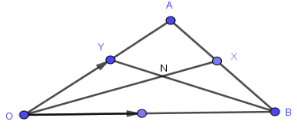
- In the figure below, OY:YA= 1:3, AX:XB=1:2, OA= a and OB =b . n is the point of intersection of BY and OX.
Determine;- OX (2 marks)
- BY (1 mark)
- Given that BN = mBY and ON = nOX, express ON in two ways in terms of a, b, m and n (3 marks)
- Find the values of m and n (4 marks)
- In the figure below, OY:YA= 1:3, AX:XB=1:2, OA= a and OB =b . n is the point of intersection of BY and OX.
-
- In a geometrical progression the sum of the second and third term is 12 and the sum of the third and fourth terms is −36. Find the first term and the common ratio. (4 marks)
- In an arithmetic progression the 12th term is 25 and the 7th term is three times the second term, find;
- The first term and the common difference (4 marks)
- The sum of the first 10 terms of the arithmetic progression.(2 marks)
- The table below shows the frequency distribution of marks scored by students in a test.
Marks 1-10 11-20 21-30 31-40 41-50 Frequency 2 4 8 4 2 - On the grid provided, draw a cumulative frequency curve for the data. (3 marks)
- Use your graph to determine;
- The pass mark if only 6 students passed the exam. (2 marks)
- The upper quartile mark (1 mark)
- Find the percentage change if the upper quartile in b(ii) above was found by calculation. (3 marks)
- A gold urn contains 3 red balls and 4 white balls and a silver urn contains 5 red balls and 2 white balls. A die is rolled and if a 6 shows, balls will be selected at random from the gold urn. Otherwise balls are selected from the silver urn.
- Find the probability of selecting a red ball. (3 marks)
- If two balls are selected at random without replacement,
- Draw a tree diagram to represent this information. (3 marks)
- Find the probability that two balls are white. (2 marks)
- Find the probability that there is at most one white ball from the silver urn. (3 marks)
-
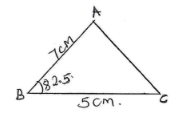
- Using a ruler and a compass only construct triangle ABC where AB=7cm, Angle CBA=82.5° and BC=5cm (4marks)
-
- Locate a point T inside the triangle which is equidistant from points A and B and also equidistant from lines AB and AC (3 marks)
- Measure TB (1 mark)
- By shading the unwanted region show the area inside the triangle where P lies if it is nearer to point B than to point A and also nearer to the line AB than line AC. (2 marks)
-
- Complete the table for y = Sin x + 2 Cos x. (2 marks)
x° 0 30 60 90 120 150 180 210 240 270 300 Sin x 0.00 1.00 0.50 −0.50 −0.87 2 cos x 2.00 0.00 −1.73 −1.73 1.00 y 2.00 1.00 −1.23 −2.23 0.13 - Draw the graph of y = Sin x + 2 cos x. (3 marks)
- Solve sin x + 2 cos x = 0 using the graph. (2 marks)
- Find the range of values of x for which y < −0.5 (3 marks)
- Complete the table for y = Sin x + 2 Cos x. (2 marks)
- A triangle ABC with vertices at A (1,-1) ,B (3,-1) and C (1, 3) is mapped onto triangle A1B1C1 by a transformation whose matrix is .Triangle A¹B¹C¹ is then mapped onto A¹¹B¹¹C¹¹ with vertices at A¹¹ (2, 2), B¹¹ (6, 2) and C¹¹ (2,−6) by a second transformation.
- Find the coordinates of A¹B¹C¹ (3 marks)
- Find the matrix which maps A¹B¹C¹ onto A¹¹B¹¹C¹¹. (3 marks)
- Determine the ratio of the area of triangle A¹B¹C¹ to triangle A¹¹B¹¹C¹¹. (1 mark)
- Find the transformation matrix which maps A¹¹B¹¹C¹¹ onto ABC (3 marks)
MARKING SCHEME
SECTION I. Answer all the questions ( 50 marks)
- A student spends 3/8 of his time playing basketball, ¼ of the remaining in playing table tennis and ¾ of the remaining time playing volleyball. The rest is spent on reading novels. What fraction of the time is spent on reading novels?
(3 marks)
3/8 → B.ball
¼ × 3/8
= 5/32
3/8 + 5/32
= 17/32
Remaining 15/32
¾ × 15/32 = 45/128
17/32 + 45/128 = 113/128
1 − 113/128
= 15/128 - Simplify; √5 − 1 (3 marks)
√5 + 1
√5 − 1 × √5 + 1
√5 + 1 √5 + 1
Numerator
6 − 2√5
Denominator
5 − 1 = 4
6 − 2√5 = 3/2 − ½√5 or 1.5 − 0.5√5
4 - Solve the equation 2 log 3 + log (x−2) = 2 log x (3 marks)
log(32(x−2)) = log x2
9(x − 2) = x2
x2 − 9x + 18 = 0
(x − 6) (x −3) = 0
x = 6
x = 3 - The base and perpendicular height of a triangle measured to the nearest millimetre are 15.0 cm and 9.5 cm respectively. Find:
- The absolute error in calculating the area of the triangle (1 mark)
A.E = 143.7275 − 141.2775Min product Actual Max product 14.95
9.4515.0
9.515.05
9.55141.2775 142.5 143.7275
2
= 1.225 - The percentage error in the area, giving the answer to 1 decimal place. (3 marks)
1.225 × 100
142.5
= 0.859 = 0.9%
- The absolute error in calculating the area of the triangle (1 mark)
- Find the value of θ, given that; ½ sin = 0.35 for 0° ≤ θ ≤ 360° (3 marks)
Sin θ = 0.70
θ = sin−1 0.70
θ = 44.43°
180 − 44.43
= 135.57 - Make Q the subject of formula P2 =
(3 marks)
P2 =
P2Q2 − P2 = Q2
P2Q2 − Q2 = P2
Q2 (P2 − 1) = P2
Q2 = P²
P2 − 1 - The coordinates of the end points of a diameter of a circle are A2,4 and B(2,6). Find the equation of the circle in the form ax2 + by2 +cx + dy + e = 0 (4 marks)
Centre
(2+4, 4+6)
2 2
(0, 5)
Radius = √((0−2)² + (5−4)²)
r = √5
(x−0)² + (y−5)² = (√5)²
x² + y² − 10y + 25 = 5
x² + y² − 10y + 20 = 0 - Kimani wants to buy a TV on hire purchase. It has a cash price of Ksh.30,000. He makes a down payment of Ksh.9,000 and 12 monthly instalments of ksh. 2,200 each. Calculate the rate of compound interest charged per month.(Give your answer to 1 dp). (3 marks)
P = 30000 − 9000
= 21000
A = 12 × 2200
= 26,400
26,400 = 21,000(1+r/100)12
1.257 = (1+r/100)12
12√1.257 = 1.0193
1.0193 = (1+r/100)
r = 1.93
r = 1.9 - Expand (3 + 3x)6 in ascending powers of x. Hence use the expansion up to the 3rd term, to find the value of (3.03)6 correct to 2 decimal places. (3 marks)
(3 + 3x)6
729 + 4356x + 10935x² + 14580x³ + 10935x4 + 4356x5 + 729x6
3 + 3x = 3.03
x = 0.01
729 + 4356x + 10935x² → 729 + 4356(0.01) + 10935(0.01)²
= 773.6535
≅ 773.62 (2dp) - The following are ages of students in a class 7,9,8,9,11,12,10 9,8,6,7,10,11,12,6,9,7, and 11.
- Complete the frequency distribution table below (1 mark)
x̄ = 162Ages x 6 7 8 9 10 11 12 No of students 2 3 2 4 2 3 2 (x − x̄) −3 −2 −1 0 1 2 3 (x − x̄)² 9 4 1 0 1 4 9
18
= 9 - Calculate the standard deviation of their ages in five years’ time. (2 marks)
V = ∑d²
N
=28/18
= 1.5
s.d = 1.247
- Complete the frequency distribution table below (1 mark)
- Find the possible values of x given that
is a singular matrix. (3 marks)
x² + 8x − 48 = 0
x² + 12x − 4x − 48 = 0
x(x + 12) − 4 (x + 12) = 0
(x + 12) ( x − 4) = 0
x = −12
x = 4 - Evaluate using the logarithm table; (4 marks)
( log 9.814 )−½ = (4.283 × (0.009478)²)½
[4.283 × (0.0094782)²] 0.9931 - The figure below is that of a circumcircle of the triangle ABC. The radius of the circle is 5cm. Given that ∠ABC = 70° and ∠ACB=40°. Calculate the area of ΔABC . (3 marks)
BC = AC ≠ a
a = 2 × 5
sin 70°
a = 10 × sin 70
A = ½ × (10sin70)² × sin 40°
A = 28.38cm² - A quantity P varies partly as the cube of Q and partly varies inversely as the square of Q. when Q = 2, P = 108 and when Q = 3, P = 259. Find the value of P when Q = 6. (3 marks)
P = Q³k + n
Q²
108 = 8k + n/4
259 = 27k + n/9
432 = 32k + n
2331 = 243k + n
−1899 = −211k
k = 9
108 = 8(9) = n/4
n = 144
P = 63(9) + 144
36
P = 1948 - The table below shows the number of insects and corresponding number of days in breeding.
Number of insects 200 300 400 500 600 700 800 900 Days 4.4 6.4 7.4 8.0 8.5 9.0 9.5 10 - On the grid provided, draw the graph of number of insects against the number of days. (1 mark)
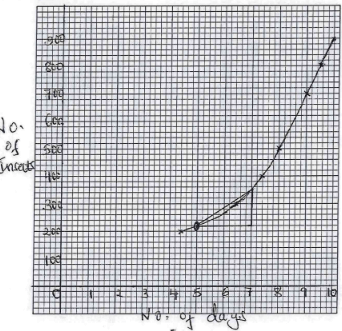
- Determine the rate of breeding between 5th and 7th day. (2 marks)
5th → 220
7th → 350
350 − 220
7−5
= 65 ± 1
- On the grid provided, draw the graph of number of insects against the number of days. (1 mark)
- Calculate the area of the minor segment of a circle of radius 5√2cm, cut off by a chord of length 10cm. (3 marks)
sin θ = 5
5√2
Sin θ = 1
√2
θ = 45°
90/360 × 3.142 × (5√2)
= 39.275
½ (5√2) × sin 90°
= 25
39.275 − 25
= 14.275
SECTION II: Answer any 5 questions from this section. ( 50 marks)
- Income rates for income earned were charged as shown in the table alongside:
A civil servant earns a monthly salary of Ksh.27,000. He was also given a house allowance of Ksh. 12,000 , transport allowance Ksh.1,800 and medical allowance Ksh.2,000. He is entitled to a family relief of Kshs. 1040 per month.
Determine:Income in Ksh. pm Rate in Ksh. Per Shs. 20 1- 8400 2 8401- 18,000 3 18,001- 30,000 4 30,000 - 36,000 5 36,000-48,000 6 48,001 and above 7 -
- His taxable income per month in Ksh. (2 marks)
27,000 + 12,000 + 1,800 + 2,000
= 42,800 - His net tax. (6 marks)
- His taxable income per month in Ksh. (2 marks)
- In addition, the following deductions were made
NHIF Ksh. 430
Loan repayment Ksh. 6500
Bank shares Ksh. 1000.
Calculate his net pay per month. (2 marks)
Total deductions
= 7930 + 7180
= 15110
42800 − 15110
= 27,690
-
-
- In the figure below, OY:YA= 1:3, AX:XB=1:2, OA= a and OB =b . n is the point of intersection of BY and OX.
Determine;- OX (2 marks)
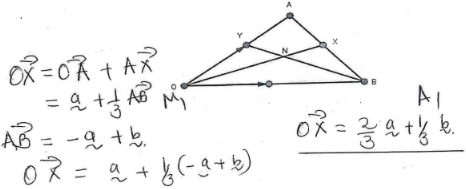
- BY (1 mark)
→
BY = ¼a − b
- OX (2 marks)
- Given that BN = mBY and ON = nOX, express ON in two ways in terms of a, b, m and n (3 marks)
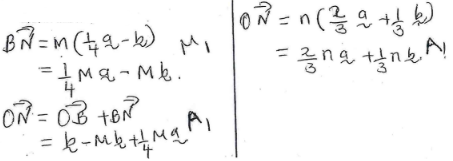
- Find the values of m and n (4 marks)
(1−m) b + ¼ma = 2/3na + 1/3nb
¼m = 2/3n
m = 8/3n .....(i)
1−m = 1/3n
3 − 3m = n
3 − 3(8/3n) = n
3 = 9n
n = 1/3
m = 8/3(1/3)
m = 8/9
- In the figure below, OY:YA= 1:3, AX:XB=1:2, OA= a and OB =b . n is the point of intersection of BY and OX.
-
- In a geometrical progression the sum of the second and third term is 12 and the sum of the third and fourth terms is −36. Find the first term and the common ratio. (4 marks)
ar + ar² = 12
ar² + ar³ = −36
ar(1+r)=12
ar²(1+r) = −36
ar² = −36
ar 12
r = −3
From ar + ar² = 12
−3a + 9a = 12
a = 2 - In an arithmetic progression the 12th term is 25 and the 7th term is three times the second term, find;
- The first term and the common difference (4 marks)
a + 11d = 25
(a + d)3 = a + 6d
a + 11d = 25
2a = 3d
a = 3/2d .......(i)
3/2d + 11d = 25
3d + 22d = 50
25d = 50
d = 2
a = 3/2(2)
a = 3 - The sum of the first 10 terms of the arithmetic progression.(2 marks)
Sn = n/2(2a + (n−1)d)
=10/2(2×3 + (10−1)2)
=120
- The first term and the common difference (4 marks)
- In a geometrical progression the sum of the second and third term is 12 and the sum of the third and fourth terms is −36. Find the first term and the common ratio. (4 marks)
- The table below shows the frequency distribution of marks scored by students in a test.
Marks 1-10 11-20 21-30 31-40 41-50 Frequency 2 4 8 4 2 C.F 2 6 14 18 20 - On the grid provided, draw a cumulative frequency curve for the data. (3 marks)
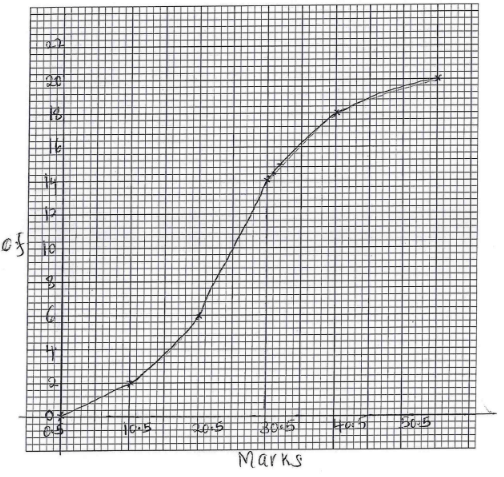
- Use your graph to determine;
- The pass mark if only 6 students passed the exam. (2 marks)
20 − 6 = 14
= 30.5 - The upper quartile mark (1 mark)
¾ × 50
¾ × 20
= 31.5 marks
= 15th value
- The pass mark if only 6 students passed the exam. (2 marks)
- Find the percentage change if the upper quartile in b(ii) above was found by calculation. (3 marks)
= 30.5 + (15 − 14) 10
4
= 30.5 + 2.5
= 33
(33 − 31.5)100 = 4.76%
31.5
- On the grid provided, draw a cumulative frequency curve for the data. (3 marks)
- A gold urn contains 3 red balls and 4 white balls and a silver urn contains 5 red balls and 2 white balls. A die is rolled and if a 6 shows, balls will be selected at random from the gold urn. Otherwise balls are selected from the silver urn.
- Find the probability of selecting a red ball. (3 marks)
1/6 × 3/7 or 5/6 × 5/7
(1/14 + 25/42) = 2/3 - If two balls are selected at random without replacement,
- Draw a tree diagram to represent this information. (3 marks)
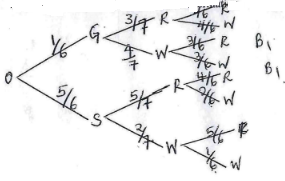
- Find the probability that two balls are white. (2 marks)
P(SWW) or P(GWW)
= (5/6 × 2/7 × 1/6) + (1/6 × 4/7 × 3/6)
5 + 1 = 11
126 21 126 - Find the probability that there is at most one white ball from the silver urn. (3 marks)
p(0) or (p(1)
P(SRR) or P(SWR) or P(SRW)
= 5/6 × 5/7 × 4/6) + (5/6 × 2/7 × 5/6) + (5/6 × 5/7 × 2/6)
= 25/63 + 25/126 + 25/126
= 50/63
- Draw a tree diagram to represent this information. (3 marks)
- Find the probability of selecting a red ball. (3 marks)
-
- Using a ruler and a compass only construct triangle ABC where AB=7cm, Angle CBA=82.5° and BC=5cm (4marks)
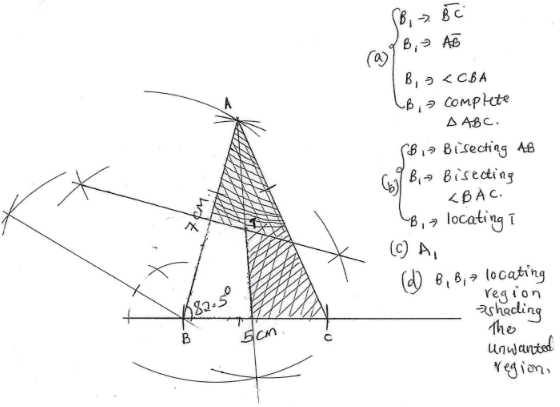
-
- Locate a point T inside the triangle which is equidistant from points A and B and also equidistant from lines AB and AC (3 marks)
- Measure TB (1 mark)
(3.7 ± 0.1 )cm
- By shading the unwanted region show the area inside the triangle where P lies if it is nearer to point B than to point A and also nearer to the line AB than line AC. (2 marks)
- Using a ruler and a compass only construct triangle ABC where AB=7cm, Angle CBA=82.5° and BC=5cm (4marks)
-
- Complete the table for y = Sin x + 2 Cos x. (2 marks)
x° 0 30 60 90 120 150 180 210 240 270 300 Sin x 0.00 0.50 0.87 1.00 0.87 0.50 0.00 −0.50 −0.87 −1.00 −0.87 2 cos x 2.00 1.73 1.00 0.00 −1.00 −1.73 −2.00 −1.73 −1.00 0.00 1.00 y 2.00 2.23 1.87 1.00 −0.13 −1.23 −2.00 −2.23 −1.87 −1.00 0.13 - Draw the graph of y = Sin x + 2 cos x. (3 marks)
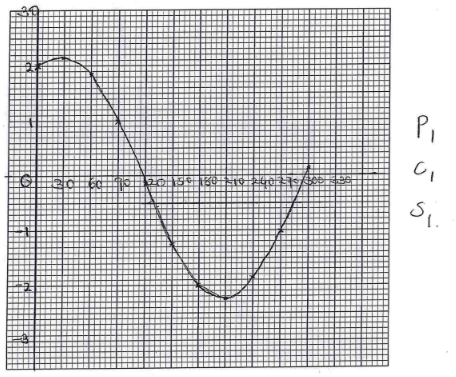
- Solve sin x + 2 cos x = 0 using the graph. (2 marks)
114 ± 2 , 294 ± 2 - Find the range of values of x for which y < −0.5 (3 marks)
132° − 280°
- Complete the table for y = Sin x + 2 Cos x. (2 marks)
- A triangle ABC with vertices at A (1,-1) ,B (3,-1) and C (1, 3) is mapped onto triangle A1B1C1 by a transformation whose matrix is .Triangle A¹B¹C¹ is then mapped onto A¹¹B¹¹C¹¹ with vertices at A¹¹ (2, 2), B¹¹ (6, 2) and C¹¹ (2,−6) by a second transformation.
- Find the coordinates of A¹B¹C¹ (3 marks)
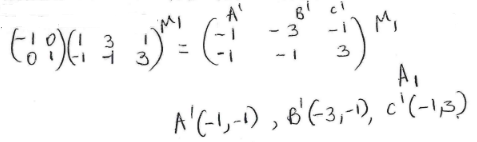
- Find the matrix which maps A¹B¹C¹ onto A¹¹B¹¹C¹¹. (3 marks)
- Determine the ratio of the area of triangle A¹B¹C¹ to triangle A¹¹B¹¹C¹¹. (1 mark)
determinant = 4
- Find the transformation matrix which maps A¹¹B¹¹C¹¹ onto ABC (3 marks)
- Find the coordinates of A¹B¹C¹ (3 marks)
Download Mathematics Paper 2 Questions and Answers - Kassu Jet Pre Mocks 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students