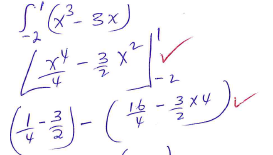Mathematics Paper 1 Questions and answers - Sukellemo Joint Pre Mock Exams 2022

QUESTIONS
SECTION 1 (50 MARKS)
Answer all the questions in the space provided below each question

1. Find the equation of a straight line passing through the points A (1,-3) and B (-2, 5).Express your answer in the form ax + by = c where a, b and c are integers. (3marks)
2. Evaluate without using mathematical tables or calculator -10÷2+6×4-8×5 (3marks)
                                                                                                -5+(-12)÷3×2
3. Solve for x in the equation Cos(2x-30)°= tan45° (3marks)
                                              Sin(3x+10)°
4. Two taps P and Q together can fill a water tank in 6 minutes. Tap P alone takes 5 minutes longer than tap Q. How many minutes does it take tap P alone to fill the tank? (3marks)
5. Given that, 27^5x-2y=243 and 81^2x-y=3, Calculate the values of x and y. (3marks)
6. A point P is mapped onto P’ by a negative quarter turn about the origin. P’ is mapped onto P’’ by a translation represented by the vector (^-2₃) . If P’’ has coordinates (11,-5) determine the coordinates of p. (3marks)
   
   
7. A metallic pipe which is 21 meters long has an internal radius of 13 cm and an external radius of 15 cm. if the density of the metal is 8620 kg/ m³, find its mass. (3marks)
8. Using logarithms evaluate ∛(82.73×0.2943²)(3marks)
                                                      613.5
9. A proper fraction is such that the denominator exceeds the numerator by 3. If 2 is subtracted from both the numerator and denominator, the fraction formed is ¹/₈ less. Determine the original fraction. (3 marks)
10. Given that OM = 2i +3j -6k and ON = -3i + 5j +k.Find the magnitude of MN to 2 decimal places. (3marks)
11. Find the range of the integral values of x in the inequality 10<3(x+2)<35 , giving your answer in the form a≤x≤b (3marks)
12. Simplify completely    2-2x    ÷  x-1  (3marks)
                                   6x²-x-12    2x-3
13. The marked price of a recliner sofa set in a furniture store was ksh 400,000.A customer bought the recliner at 10% discount. The dealer still made a profit of 20%, Calculate the amount of money the dealer paid for the recliner. (3marks)
14. Draw a line AB of length 9 cm. On one side of line AB construct the locus of a point P such that the area of triangle ABC is 13.5 cm².On this locus locate two positions of a point P1 and P2 such that
15. Given that the area of an image is four times the area of the object under a transformation whose matrix is , find the possible value of x .(3 marks)
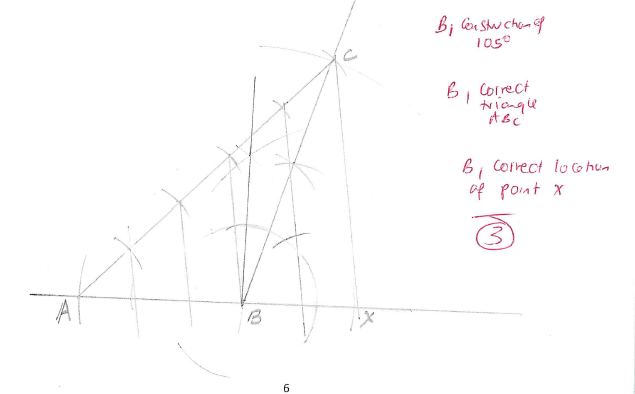
16. Construct a triangle ABC in which AB = 5cm and AC = 8cm and ∠ABC=105°. Using line AC, locate point x on AB produced such that AX: XB =3: -2. (4marks)

SECTION II (50 MARKS)
Answer only five questions in this section

17. The table below shows the weekly salary (k£) paid to workers in a school.
    

    Salary (k£)	50≤x≤100	100≤x≤150	150≤x≤250	250≤x≤350	350≤x≤500
    No. of Workers	25	27	30	26	24

    1. Calculate the differences between the mean and the median. (6 marks)
    2. Draw a frequency polygon to illustrate the above information. (4marks)
       
18.      
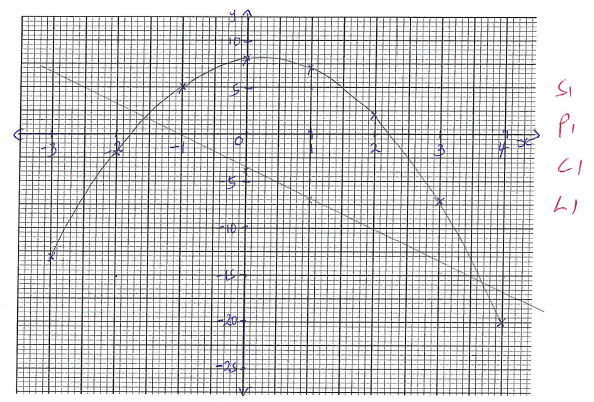
    1. Complete the table of values for the equation, y=-2x^(2 )+x+8. (2marks)
       

       x	-3	-2	-1	0	1	2	3	4
       y

    2. Use the values above to draw the graph of y=-2x²+x+8 . (3marks)
       
    3. Using the graph drawn above Solve the equations:-
       1. 2x²=x+8 (2marks)
       2. -2x²+4x+12=0 (3marks)
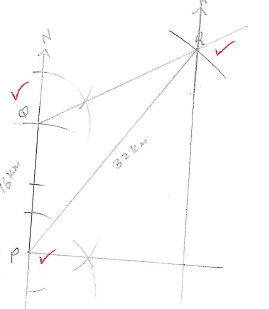
19. Three towns P, Q and R are such that Q is 16 km north of P and the distance of R is 12 km from P and on a bearing of 60º from Q.
    1. Using a scale of 1cm to represent 4km, Make a scale drawing showing the relative positions of the three towns. (3marks)
    2. Using the scale drawing above, find the
       1. Distance of R from Q. (1mark)
       2. Bearing of P from Q. (1mark)
       3. How far town R is east of Q (1mark)
    3. A Passenger in an aero plane after take-off from town R spotted town P at an angle of depression of 48º, by means of a scale drawing determine the vertical height of the plane at town R. (3marks)
20.      
    1. The equation of a straight line L1 is of the form 3y+2x=5.L1 is perpendicular to L2 and meets it at the point where X=-2, determine the equation of L2 in the form y = mx+c where m and c are constants. (5marks)
    2. L3 is parallel to the line L2 and passes through the point (-3,2).,find the equation of L3, leaving your answer in its double intercept form. (3marks)
    3. Determine the angle of inclination of L2 to the Y-axis. (2marks)
21. The points P, Q, R and S, have position vectors 2p, 3p, r and 3r respectively, relative to an origin O. A point T divides PS internally in the ratio 1:6.
    1. Find, in its simplest form OT, QT and TR in terms of p and r. (6 marks)
    2. Show that the points Q, T and R, are collinear. (3marks)
    3. Determine the ratio in which T divides QR. (1mark)
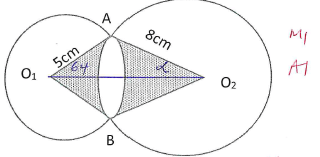
22. In the figure below, O₁ and O₂ are the centers of the circles whose radii are 5 cm and 8 cm respectively. The circles intersect at A and B and angle AO₁O₂ = 64˚.
    
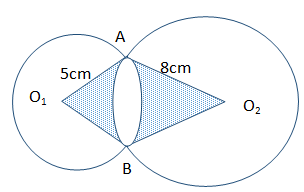
    Calculate the area of the:-
    1. Sector
       1. AO₁B (2marks)
       2. AO₂B (3 marks)
    2. Intersecting region. (3marks)
    3. The shaded region. (2marks)
23.      
    1. Find the x –intercept of the curve y = (x+2) (x-1)². (1mark).
    2. Find the gradient function of the curve y = (x+2) (x-1)² (2marks)
    3. Find the co-ordinates of the turning point. Hence sketch the curve y= (x+2) (x-1)². (4 marks)
    4. Calculate the exact area enclosed by the curve and the x - axis (3marks)
24. P and Q are two points on latitude 40°N.Their longitudes are 30°E and 150°W respectively. Find to one decimal place :( Take the radius of the earth = 6370km andπ=²²/₇)
    1. The distance in km between P and Q along the parallel of latitudes. (2marks)
    2. The shortest distance along the earth’s surface between P and Q in km. (3marks)
    3. A weather forecaster reports that the center of a cyclone at (40°N, 60°W) is moving due north at 24 knots. How long will it take to reach a point (45°N, 60°W). (2marks)
    4. A plane leaves P at 2.15 pm at a speed of 350 knots to town R (40°N, 65°E). Determine the time at R when the plane arrived. (3marks)

MARKING SCHEME

1. Gradient = ⁵/_-2 = ³/_-1 = ^-8/₃
   y - 5 - ^-8/₃
   x + 2
   3(y - 5) = -8(x + 2)
   3y - 15 = -8 - 16
   3y  + 8x = -1
2. Numerator = -5 + 24 - 40
   -21
   den. = -5 - 8 
   = -13
   ^-21/_-13
   = 1⁸/₁₃
3. cos(2x - 30)º = sin(3x + 10)º
   cos(2x - 30)º = cos 90 -(3x + 10)
   2x - 30 = 90 - (3x + 10)
   2x - 30 + (3x + 10) = 90
   5x - 20 = 90
   5x = 110
   x = 22
4. ¹/_x+5 + ¹/_x = ¹/₆
   6(x + x + 5) = x(x + 5)
   6x + 6x + 30 = x2 + 5x
   -7x - 30 = 0
   - 10x + 3x - 30 = 0
   x(x - 10) + 3(x - 10) = 0
   (x + 3)(x - 10) = 0
   x = -3 or 10
   Top P = 5 + 10
   =15mins
5. 3^{3(5x - 2y)} = 3⁵
   3(5x - 2y)= 5
   15x - 6y = 5
   3⁴(2x - y) = 3¹
   4(2x - y) = 1
   (15x - 6y = 5)4
   (8x - 4y = 1)6
   60x - 24y = 20
   48x - 24y = 6
   12x = 14
   x = 1¹/₆
   8x⁷/₆ - 4y = 1
   ⁵⁶/₆ - 4y = 1 
   8¹/₃ = 4y
   2¹/₁₂ = y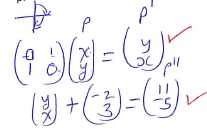
6. 
   
   y - 2 = 11
   y = 13
   x + 3 = -5
   x = -8
   P(-8, 13)
7. External volume - Internal volume
   ²²/₇ x 15² x 2100 - ²²/₇ x 13² x 2100
   ²²/₇ x 2100 (225 - 169)
   ²²/₇ x 2100 x 56
   369,600cm³
   0.3696m³
   Mass = 8620 x 0.3696
   = 8620 x 3696
                  1000
   3185.952
   = 3186kg
8. 
   

   No	Log
   0.29432 82.73 613.5 0.2269	T.4688 x 2 2.9376 1.9177 +  0.8553 2.7878- 2.0675 2.0675 = 3/3 + 1.0675 = T + 0.3558 33 T.3558

9. ^x/_y 
   y - x = 3
   y = x = 3
   y = 3 + x
   x - 2 = ^x/_y - ¹/₈
   y - 2 
     x - 2  =  x    - ¹/₈
    3+x-2    3+x
   (x - 2) (x + 3 )8 = x (x + 1)8-((x+1)(x + 3))
   (x² + x - 6)8 = 8x² + 8x - (x² + 4x + 3)
   8x² + 8x - 48 = 8x² + 8x - x² - 4x - 3
   0 = -y² -4x + 45
   x² + 4x - 45 = 0
   x² + 9x - 5x - 45 - 0
   x(x + 9) -5(x + 9) = 0
   (x - 5)(x + 9) = 0
   x = 5 or -9 
10. MN = √(-3-2)² + (5-3)² + (1-6)²
    √25+ 4 + 49
    √78
    8.832
    8.83
11. 10<33(x + 2)
    10<3x + 6
    4<3x
    1¹/₃ < x
    3x + 6 < 35
    3x < 29
    x < 9²/₃
    
    2≤x≤9
12.         2(1-x)         
    6x² - 9x + 8x - 12
          -2(x - 1)        
    3x(2x-3)+4(2x-3)
         -2(x-1)    
    (3x+4)(2x-3)
    =  -2   
      3x+4
13. 100% = 400000
    90% = 90 x 400000
                     100
    = 360000
    120% = 360000
    100% = 100 x 360000
                       120
    = 300000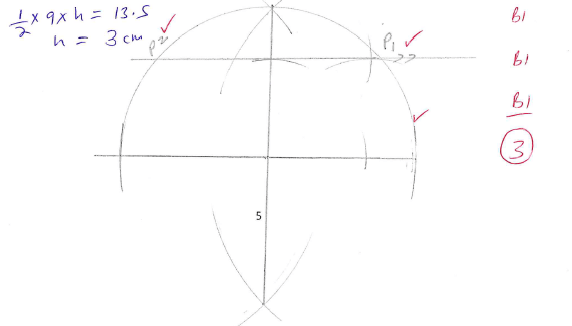
14. 
    
    ½ x 9 x h = 13.5
    h = 3cm
15. x² - ((x-4)(x+8)) = 4
    x² - (+4x - 32) = 4
    x²- x² - 4x + 32 = 4
    - 4x = -28
    x = 7
16.     
    
17.    
    1. 
       

       0-50	f	x	fx	cf	fd
       50-100	25	75	1875	25	0.5
       100-150	27	125	3375	52	0.54
       150-250	30	200	6000	82	0.3
       250-350	26	300	7800	108	0.26
       350-500	24	425	10200	132	0.16
       500-650	Σf=132		Σfx= 29250

       Mean = 29250
       132 
       = 221.60
       Median = 66th position
       150 + 82
       150 + (66 - 52) x 100
                    200
       221.60 - 157
       = 64.60
    2.    
       
18.    
    1.    
       

       x	-3	-2	-1	0	1	2	3	4
       y	-13	-2	5	8	7	2	-7	-20

    2.     
       
    3.      
       1. 2x² + x + 8 = 0
          -2x² + x + 8 = y
          0 = y
          x = -1.78 or x =2.2
       2. -2x² + x + 8 = y
          -3x - 4 = y
          x = -1.55
          x = 3.67
19.      
    1.     
       
    2.    
       1. 5.3cm = 5.3 x 4 = 21.2km 
          21 ± 0.4
       2. 215º
          214 ± 1 
       3. 4.7cm = 4.7 x 4 = 18.8km
          18.1 ± 0.4
    3.     
       
20.      
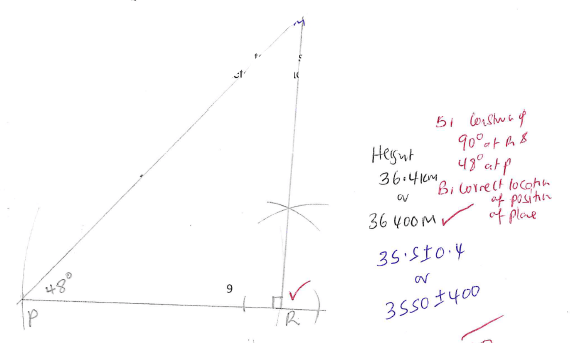
    1. 3y = -2x + 5
       y = ^-2/₃x + ⁵/₃
       Gr = ³/₂
       at x = -2
       y = ⁴/₃ + ⁵/₃= ⁹/₃ = 3
       (-2, 3)
       y - 3 = ³/₂
       x + 2 
       2y - 6 = 3x + 6 
       2y = 3x + 12
       y = ³/₂x + 6
    2.  y- 2  = ³/₂
       x + 3
       3(x + 3) = 2(y - 2)
       3x + 9 = 2y - 4
       3x - 2y = -13
       ^3x/_-13 + ^2y/₁₃ = 1
          x   +  y   = 1
       ^-13/₃    ¹³/₃ 
         x    +  y  = 1
       -4¹/₃   6½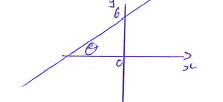
    3. 
       
       tanθ = ³/₂
       θ = 56.31º
       90 - 56.31º = 33.69º
       angle 33.69º or 146 .31º
21.      
    1. 
       
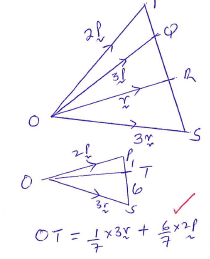
       OT = ³/₇r + ¹²/₇p
       QT = QO + OT
       = -3p +³/₇r + ¹²/₇p
       = ³/₇r - ⁹/₇p
       TR = TO + OR
       = -³/₇r - ¹²/₇p + r
       = ⁴/₇r -¹²/₇p
    2. QT = ³/₇(r - 3p)
       TR = ⁴/₇(r - 3p)
       ⁴/₇QT = ³/₇TR
       4QT = 3TR
       QT//TR
    3. QT/TR = ¾
       QT:TR = 3:4
22. 
         
    1.      
       1. ¹²⁸/₃₆₀ x ²²/₇ x 25
          27.94
       2. ⁸/_sin64 = ⁵/_sinx
          sin x = 5 x sin64
                           8
          = 0.5617
          = 34.18º
          2x = 68.36º
          68.36 x ²²/₇ x 64
           360
          = 38.19
    2. (27.94 - x 25 x sin128) + 38.19 - x 64 x sin68..36
       27.94 - 9.850                        38.19 - 29.74
       18.09 + 8.45
       26.54
    3. 9.850 + 29.74 - 26.54
       39.59 - 26.54
       13.05
23.        
    1. (x+2)(x-1) = 0
       x = 1 or -2
    2. y = (x+2)(x² - 2x + 1)
       y = x³ - 2x² + 2x² + x - 4x
       y = x³ - 3x
       ^dy/_dx = 3x² - 3 
    3. 3(x² -1) = 0
       3(x-1)(x+1) = 0
       3(x-1)(x-1) = 0
       x = 1 or -1
       when x = 1, y = 0
       (1,0)
       d²y = 6x at x=1
       dx²
       = 6
       (1,0)minimal
       when x = -1
       y = (-1+2)(-1-1)²
       y = 4
       (-1,4)
       d²y = 6x at x = -1
       dx²
       2²y = -6
       dx²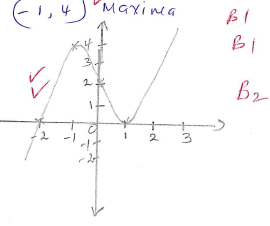 
       
    4. 
       
       -1.25 - (-2)
       0.75
24.      
    1. 
       
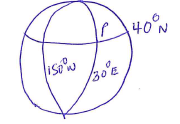
       dif in longitude = 180
       180 x ²²/₇ x 2 6370 x cos40
       360
       = 15336.2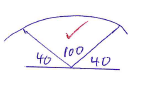
    2. 
       
       100 x ²²/₇ x 2 x 6370
       360
       = 8272.7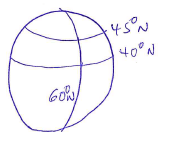
    3. 
       
       differences in latitude = 45-40
       = 50
       = 5 x 60 = 300NM
       Time = ³⁰⁰/₂₄
       = 12.5hrs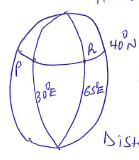
    4. 
       
       differences in longitude = 65-0
       = 35º
       24hrs = 360º
       35 x 24 
         360
       2hrs 20mins
       Distance = 35 x 60 x c0s40
       = 1,608.7NM
       Time = 1608.7
                     350
       = 4.596hrs
       4hrs, 36 mins 
       = 8.11p.m