Mathematics Paper 2 Questions and Answers - Sukellemo Joint Pre Mock Exams 2022

QUESTIONS
SECTION I (50 MARKS)
Answer all the questions from this section

1. The expression (1 + ^x/₂) is taken as an approximation for . Find the percentage error in doing so if x = 0.44. (Give answer correct to 2 d.p) (3 Marks)
2. Express the following in surd form and simplify by rationalizing the denominator. (3 Marks)
              1          
   cos60º - sin45º
3. Make q the subject of the formula ( 3 Marks)
   P= ³√nq-m
              q
4. The data below shows the age of 10 pupils picked at random in a primary school 6, 11, 13, 14, 8, 7, 12, 20, P and 9 if  ∑fx²= 1360. Determine the value of P hence, find the standard Deviation to 3d.p (4 Marks)
5. The volume, V of a cylinder varies jointly as its height, (h) and the square of its radius, (r), Calculate the percentage increase in its volume (V), when radius increases by 5% and height, h increases by 10%. (3 Marks)
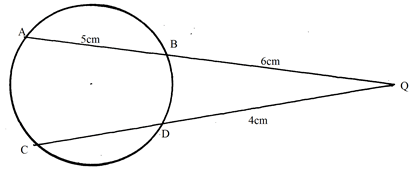
6. Chords AB and CD in the figure below intersect externally at Q. if AB = 5cm BQ = 6cm and DQ = 4cm, calculate the length of chord CD. (2 Marks)
   
7. Jane can do a piece of job in 4 days while Mary can do the same piece of work in 7 days. Mary and Jane did the job together for two days before Jane fell sick. Mary was left to complete the job. How long did it take to do the job? (3 Marks)
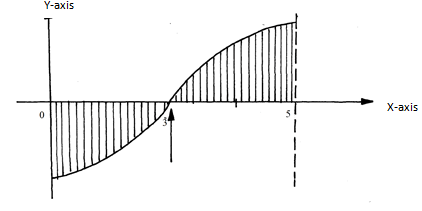
8. The sketch below represents the graph of y=x²-x-6.Find the area bounded by the curve,  x-axis, y-axis and the line x=5. (3 Marks)
   
9. Use matrix method to determine the co-ordinates of the point of intersection of the two lines. 3x-2y=13, 2y+x+1=0 (3 Marks)
10. The figure below shows an arc of a circle through three points A, B and C.
    
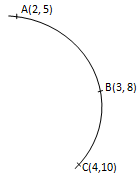
    Calculate the co-ordinates of the centre of the circle. (4 Marks)
11. A bag contains 4 white balls and 5 Red balls of similar shape and size. Two balls are picked at random without replacement. Find the probability that both balls are:
    1. White (1 Mark)
    2. Of different colour (2 Marks)
12. A point P (2,-3) undergoes transformation represented by the matrix (³₀ ³₁) .Find the co-ordinate of the image of P. (2 Marks)
13. Expand (2 + x)⁶ up to the fourth term. (2 Marks)
    Hence use the above expansion to evaluate (1.96)6 correct to 4 d.p. (2 Marks)
14. Find the value of x in the equation 10sin²x - 7cos x + 2  = 0 for the range  270°≤x ≤360° (3 Marks)
15. Find the value of x in (3 Marks)
    Log(x-2) + log (x+1) = 1 + log 4
16. The sum of two numbers is 9. The sum of the square of the number is 41. Find the numbers (4 Marks)

SECTION II (50 MARKS)
Answer FIVE questions ONLY from this section

17. The table below shows the taxation rates for income earned.
    

    Income in ksh pm	Tax rates (%)
    1 – 9680 9681 – 18800 18801 – 27920 27921 – 37040 Excess over 37041	10 15 20 25 30

    In that year, Mr. Hamisi paid a net tax of KSh. 5,512 per month. He gets a house allowance of KShs. 10,000, medical allowance of KShs. 2400 and acting allowance of KShs. 2820 per month. He was entitled to a monthly personal relief of KShs. 162. He has a life insurance policy for which he pays a monthly premium of KSh. 1,500 and claims a relief at a rate of 10% of the premium paid per month. The following deductions also made every month.
    1. N.H.I.F. KSh. 320
    2. Co-operative society shares KSh. 6000
    3. Union dues KSh. 200
       1. Calculate Mr. Hamisi’s monthly basic salary in KSh. (7 Marks)
       2. Calculate his net monthly salary. (3 Marks)
18. A jet leaves town P(30°S, 26°W) at 2.00 p.m on Monday and flew due \north to town Q(50°N,26°W).
    1. Calculate the distance covered by the jet in Km. ( take ∏=²²/₇ and R=6370) (3 Marks)
    2. After 35 min stoppage at town Q the jet flew due East to town R a distance of 2500 nautical miles from town Q.
       Find
       1. the position of town R (3 Marks)
       2. The local time the jet landed at R if its average speed for the whole journey is 1000km/h.
          (Take 1nm=1.853km) (4 Marks)
19. Use a ruler and a pair of compasses only in all constructions in this question.
    1. Construct the rectangle ABCD such that AB = 7.2cm and BC = 5.6cm. (3 Marks)
    2. Constructs on the same diagram the locus L1 of points equidistant from A and B to meet with another locus L2 of points equidistant from AB and BC at M. Measure the acute angle formed at M by L1 and L2. (3 Marks)
    3. Construct on the same diagram the locus of point K inside the rectangle such that K is less than 3.5cm from point M. Given that point K is nearer to B than A and also nearer to BA than BC, shade the possible region where K lies. Hence calculate the area of this region. Correct to one decimal place. (4 marks)
20.      
    1. The first term of a geometric progression is 36.the sum of the first three terms is 27.
       Calculate the common ratio and the value of the second term  (4 Marks)
    2. The first term of an AP is 2.the first term of a geometric sequence is also 2 and its common ratio equals the common difference of the arithmetic sequence. The square of the fifth term of arithmetic sequence exceeds the third term of the geometric sequence by 2. Find the common difference and the sum of the first 50 terms of an AP(6 Marks)
21.    
    1. Draw triangle PQR whose vertices are P(1,1) Q(-3,2) and R(0,3) on the grid provided. (1 Mark)
       
    2. Find the coordinates of triangle P1Q1R1 the image of triangle PQR under the transformation whose matrix is  (³₁ ⁰₁). Draw triangle P1Q1R1. (3 Marks)
    3. P1Q1R1 is then transformed onto P2Q2R2 by the transformation with matrix 
       
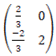
       Find the coordinates of P2Q2R2 and draw triangle P2Q2R2 (3 Marks)
    4. Describe fully a single transformation which maps PQR onto P2Q2R2. Find the matrix of this transformation (3 Marks)
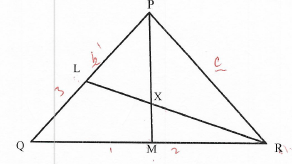
22. In the triangle PQR below, L and M are points on PQ and QR respectively such that PL: LQ=1:3 and QM:MR=1:2, PM and RL intersect at X, given that PQ = b and PR = c,
    
    
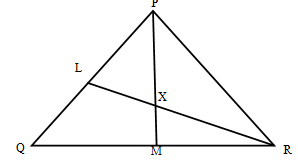
    1. Express the following vectors in terms of b and c
       1. QR (1mark)
       2. PM (1mark)
       3. RL (1mark)
    2. By taking PX = hPM and RX = kRL where h and k are constants find two expressions of PX in terms of h, k, b and c. Hence determine the values of the constant h and k. (6marks) 
    3. Determine the ratio LX: XR (1mark)
23.    
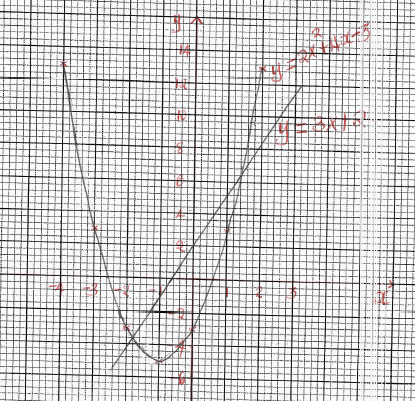
    1. Complete the table below for the function y=2x² + 4x -3 (2 Marks)
       

       x	-4	-3	-2	-1	0	1	2
       y					-3

    2. On the grid provided, draw the graph of the function y=2x² + 4x -3 for -4≤ x ≤ 2 using the scale of 1cm to represent 1 unit on axis and 1cm to represent 2 units on y-axis.   (3 Marks)
       
    3. Use the graph above to: 
       1. Determine the roots of the equation 2x² + 4x -3=0 (2 Marks)
       2. Solve the equation 2x² +x -5 =0 (3 Marks)
24. The acceleration of a particle, t seconds after passing a fixed point P is given by a = 3t – 3. Given that the velocity of the particle when t = 2 is 5m/s, find;
    1. Its velocity when t = 4 seconds   (3 Marks)
    2. Its displacement at the time in (a) above (3 Marks)
    3. The displacement during the third second  (4 Marks)

MARKING SCHEME

1. 1 + 0.44
           2
   1 + 0.22 = 1.22
   √1 + 0.44
   = 1.2
   Error = 122 - 1.2
   = 0.02
   0.02 x 100
    1.2
   = 1.67%

2.      1     = 22
   ½ - ¹/₁₂ 
      1     =  2√2  
   √2-2      √2-2
    2√2
   2√2 x √2+2
   √2-2   √2+2
   4 + 4√2
      -2
   = -2-2√2

3. p³ = nq - m
              q
   p³q = nq - m
   p³q - nq = -m
   q(p³ - n) =   -m   
     p³ - n     p³ - m
   q =  -m  
         p³-n

4. 36 + 49 + 64 + 81 + 100 + 121 + 144 + 169 + 196 + 400 + p2
   1260 + p² = 1360
   p2 = 100
   p = 10
   s.d = √∑fx² - (∑fx)²
               ∑f        ∑f
   √1360 - (10)²
       10      10 
   = √136 - 121
   = √15
   = 3.873

5. v x πr²h
   v = πr²h
   v₁ = πr₁²h₁
   = π(1.05)² x 1.1πr²h
   V₁ = 1.1025 x πr²h
   = 1.21275v
   = 1.21275v - v
             v
   = 21.275%

6. AQ x QB = CQ x QD
   11 x 6 = (x + 4)4
   66 = 4x + 16
   4x = 50
   x = 12.5

7. (¼ x ¹/₇)^{2
   11}/₂₈ x 2
   = ¹¹/₄ work donw
   = ³/₁₄
   1 day = ³/₁₄
   =³/₁₄ x ⁷/₁ = 1½
   1½ + 2 = 3½ days

8. 
   
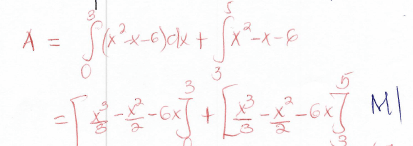
   (²⁷/₃ - ⁹/₂ - 18)-(0) + (¹²⁵/₃ - ²⁵/₂ - 30) - (²⁷/₃ - ⁹/₂ - 18)
   (-13.5)t - ⁵/₆ + 13½
   = 13½ + 12²/₃
   = 26¹/₆ sq units

9. 
   
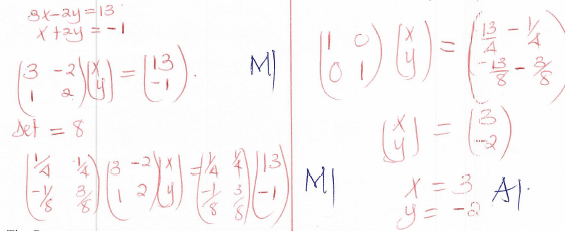
   3x - 2y = 13
   x + 2y = -1

10. (2+3 , 5+8) = (2.5 , 6.5)
      2        2
    (3+4 , 8+10) = (3.5 , 9)
       2        2 
    gradient AB = 8-5  = 3
                          3-2
    y - 6.5 = ¹/₃
    x - 2.5
    3y  - 19.5 = -x + 2.5
    3y + x = 22
    gradient BC = 10-8 = 2
                           4-3
     y-9  = -½
    x-3.5
    2y - 18 = -x + 3.5
    2y + x = 21.5
    3y + x = 22
    2y + x = 21.5
    y = 0.5
    2(0.5) + x = 21.5
    1 + x = 21.5
    x = 20.5
    (20.5 , 0.5)

11.      

    1. ⁴/₉ x ³/₈ = ¹/₆

    2. (⁴/₉ x ⁵/₈) + (⁵/₉ x ⁴/₈)
       = ⁵/₁₈ + ⁵/₁₈
       = ⁵/₉

12. (³₀ ⁰₁)(²_-3) = (⁶_-3)
    p1(6,-3)

13.      

    1. 2⁶ + 6 (2³)x + 15(2)⁴x² + 20(2)³x³
       = 64 + 102x + 240x² + 160x³

    2. (2+x)⁶ = (2-0.04)⁶
       x = -0.04
       64 + 192(-0.04) + 240(0.04)² + 160(-0.04)³
       64 - 7.68 + 0.384 - 0.01024
       = 56.6938

14. 10(1 - cos²x) - 7cosx + 2 = 0
    10 - 10cos²x - 7cosx + 2 = 0
    10cos²x + 7cosx - 12 = 0
    10y2 + 15y - 8y - 12 = 0
    5y (2y + 3)-4(2y + 3) = 0
    (5y - 4)(2y + 3) = 0
    y = ⁴/₅ or 2y = -3
    y = 0.8
    cos x = 0.8
    x = 36.87
    360 - 36.87
    = 323.13

15. logx -2 + logx+1 = log10 + log4
    log((x-2)(x-1)) = log(10x4)
    (x-2)(x-1) = 40
    x2 - x - 42 = 0
    x(x-7) +6(x-7)=0
    x=7
    log(x-2)+log(x+1) - log4=1
    log(x-2)(x+1) = 1
               4
    (x-2)(x+1)=10
          4
    (x-2)(x+1)=40
    x²-x-42=0
    x =7

16. x+y = 9
    x² + y² = 41
    y = 9-x
    x² + (9-x)² = 41
    x² - 9x + 20 = 0
    x(x-5) -4(x-5) = 0
    (x-4)(x-5) = 0
    x = 4 or x = 5
    when x = 4 
    y = 5
    when x = 5
    y =  4

17.        

    1. gross tax = 5512 + 162 + 150 
       = 5824
       9680 x 0.1 = 968 
       9120 x 0.15 = 1368
       9120 x 0.2 = 1824
       y x 0.25 = 1664
       y = 6656
       27920 + 6656
       = 34576
       34576 - (10000+2400+2820)
       = 19356

    2. 34576 - (5512 + 320 + 6000 + 200 + 1500)
       = 34576 - 13532 
       = 21,044

18.      

    1. Angle diff = 30 + 50 = 80º
       PQ =  80  x 2 x ²²/₇ x 6370
                360
       = 8898km

    2.      

       1. x x 60cos50 = 2500
          x =  2500  
              60cos50
          = 64.82º
          64.82º - 26º = 38.82
          R(50ºN , 38.82ºE)

       2. Total distance = (8898 + (2500 x 1.853))
          = 13530.5km
          Time taken = 13530.5
                                  1000
          = 13.5305hrs
          Local time at R = 2.00 + 13.5305hrs + 35min + (4x64.82)
                                                                                         60
          8.26amTues

19.    
    
    

    1.  

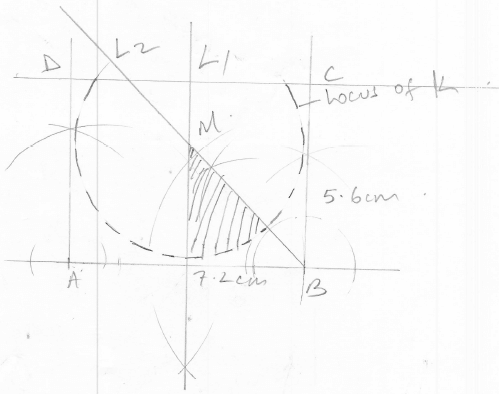
    2. 45º

    3. ⁴⁵/₃₆₀ x ²²/₇ x 3.5² = 4.8125cm²

20.      

    1. a + ar + ar² = 27
       36 + 36r + 36r² = 27
       36 + 36r + 9 = 0
       4r² + 4r + 1 = 0
       2r + 1 = 0
       r = -½
       2nd term = -½ x 36
       = -18

    2. a = 2 
       r = d
       (a+4d)² = 2r² + 2 
       (2+4d)2 = 2d + 2
       4 + 16d + 16d² = 2d² + 2 
       14d² + 16d + 2 = 0
       7d² + 8d + 1 = 0
       7d² + 7d + d + 1 = 0
       7d(d+1)+1(d+1)=0
       (7d+1)(d+1)=0
       d = -¹/₇ or d = -1
       S50 = ⁵⁰/₂{4 + (50-1)-1}
       = 25(4-49)
       = -1125
       or 
       ⁵⁰/₂{4+(50-1)-¹/₇}
       = 25(-3)
       = -75

21.     

    1.  
       

    2. 
       
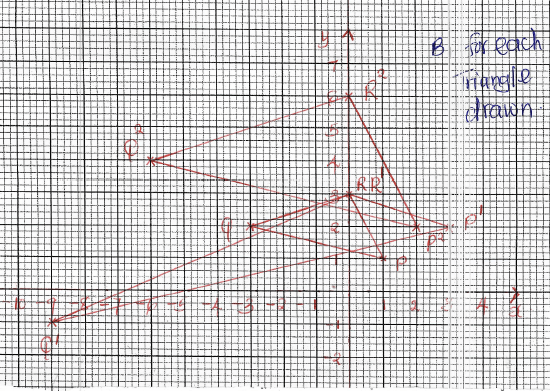
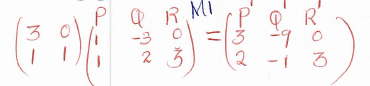
       P¹(3,2)
       Q(-9,-1)
       R(0,3)

    3. 
       
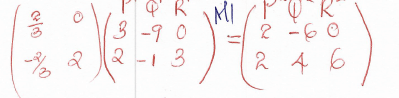
       P²(2,2) 
       Q²(-6,4)
       R²(0,6)

    4. 
       
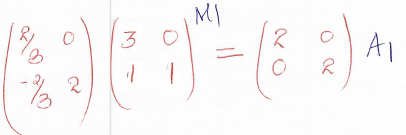
       Enlargement centre (0,0) scale factor 2

22.    
    
    

    1.      

       1. -b+c

       2. b + ¹/₃(-b+c)
          = ²/₃b + ¹/₃c

       3. b-c-¾b
          =¼b-c

    2. px = h(²/₃b + ¹/₃c)
       = ²/₃hb + ¹/₃hc
       px = c + kkb
       ²/₃hb + ¹/₃hc = (1-k)c + kb
       ²/₃h = k = k = ⁸/₃h
       ¹/₃h = 1-k
       ¹/₃h = 1 - ⁸/₃h
       ^3h/₃ = ¹/₃
       h = ¹/₃ 
       k = ⁸/₉

    3. 1:8

23.       
24. 1.     
       

       x	-4	-3	-2	-1	0	1	2
       y	13	3	-3	-5	-3	3	13

    2.  
       
    3.       
       1. x = -2.6
          x = 0.6
       2. y = 2x² + 4x - 3
          0 = 2x² + x - 5
          y =3x + 2
          x = -1.8
          x = 1.4
25.    
    1. a = 3t - 3
       v = 3t² - 3t + c
             2
       5 = ³/₂(2)² - 3(2) + c
       v = ³/₂t² - 3t + 5
       v = ³/₂(4)² - 3(4) + 5
       = 24 - 12 + 5
       = 17m/s
    2. S = t ³ - ³/₂t² + 5t +c
             2
       s = 0    t = 0
       c = 0
       S = t ³ - ³/₂t² + 5t
             2
        4 ³ - ³/₂(4)² + 5(4)
        2
       = 32 - 24 + 20
       = 28m
    3.  
       
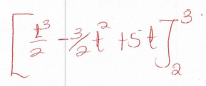
       ( 3 ³ - ³/₂(3)² + 5(3)) - ( 2 ² - ³/₂(2)² + 5 (2))
         2                                 2
       = (²⁷/₂ - ²⁷/₂ + 15) - (2 - 6 + 10)
       = 15 - 6
       =9M