Instructions to Candidates
- This paper consists of two sections; Section I and Section II.
- Answer all qUestions in Section I and only five qUestions from Section II.
- Show all the steps in your calculations, giving the answers at each stage
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
- Candidates should answer the questions in English.
SECTION I(50 marks)
Answer all the questions in this section in the spaces provided.
- State the Amplitude, the Period and the Phase angle of the function :
y = 4/3 Sin (½x + 15)°. (3marks) - Three quantities P, Q and r are such that P varies directly as Q and Inversely as the fifthroot ofr. WhenP = 1.5, Q= 9 and r= 32. Determine the equation connecting P, Q and r. (3marks)
- Omollo intends to buy a plot of land which cost Ksh.1450000. He borrows the moneyfromafinancialinstitution that charges an interest rate of r% per annum compounded quarterly.Calculate thecompoundinterest r% p.a if he payed back a sum os Ksh. 1836817 (3marks)
- Given that O is the origin , OA = 3i − 2j − 4k and OB = 4i + 5j − 2k. If a point X divides AB externally in the ratio 3 : −2. find AX (3marks)
- Without using calculators or mathematical tables, express in surd form and simplify. (3marks)
√52
2 − cos 750◦ - In the diagram below,AB and CD are chords of a circle. A point P is on the circumference of the circle.
- Construct the circle. (3marks)
- Construct the tangent to the circle passing through point P. (1mark)
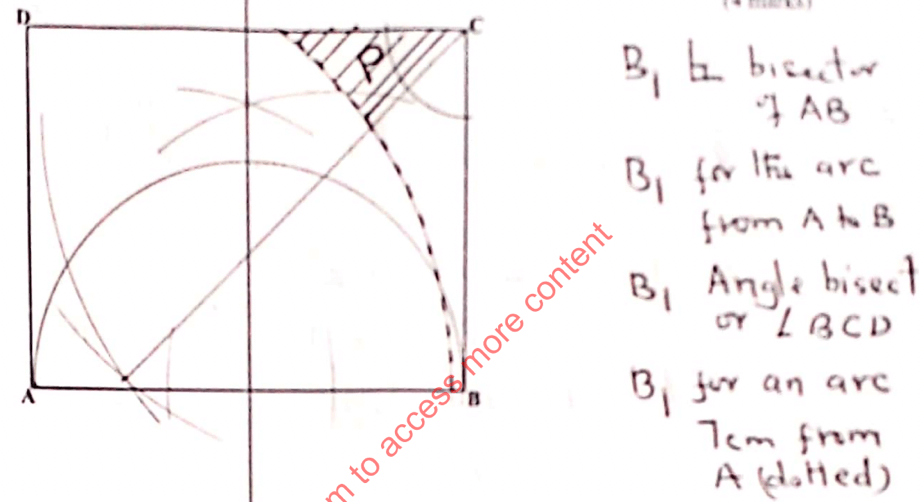
- Given the rectangle ABCD below, locate and shade a region within the rectangle in which a variable point P must lie given that P satisfies the following conditions: (4marks)
- AP ≥ BP
- ∠APB ≤ 900
- P is closer to DC than BC
- AP > 7 cm
- Use binomial expansion to simplify (3marks)
[√3 + 5]4 + [√3 − 5]4 - The table below represents a relationship between two variables P and T, connected by the equation, P = aT+ b where a and b are constants.
On the grid provided draw the line of best fit for the data.T 0.1 0.2 0.3 0.4 0.5 0.6 P 6.2 5.6 4.8 4.0 3.4 2.7
Use your graph to find the value of P when T = 0. (1mark) - Solve without using mathematical tables or calculator
4sin2(2x + 10°) = 3 for 0° ≤ x ≤ 180° (3marks) - Nine students scored some marks in a random assessment test whose deviations from the mean were. 5 , −2, 2, 1, z , −3, −2, −4, 0. Given that,the mean of the scores is 13. Find z and the quartile deviation. (4marks)
- At Maranda High School, Magwa House can accommodate only 144 students,both junior andseniorstudents. The number of junior students must be at least 90 while the number of seniors must belessthana third of the total capacity. Taking x to represent number of the junior students and y to represent the number of seniors, write down all the inequalities representing this information. (3marks)
- A coffee blender mixes two types of coffee, X which costs Ksh. 125 and Y which costs Ksh. 160. Shesellsthe mixture at Ksh. 182.5 thereby making a profit of 25%. Find the ratio X:Y at which she mixed the two types of coffee. (3marks)
- Truncate 3645986 correct to 3 significant figures.Hence calculate the percentage error arising from the truncation. (2marks)
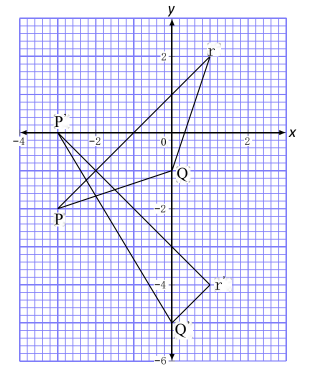
- On the grid below, triangle P’Q’R’ is the image of triangle PQR under a certain transformation. Describethe transformation. (2marks)
- Find the radius and the co-ordinates of the centre of the circle whose equation is (3marks)
½x2 + ½y2 = 3x − 5y − 9
SECTION II(50 marks)
Answer only five questions from this section in the spaces provided.
-
- A fair tetrahedron with faces marked 1,2,3 and 4 and a fair die are tossed together and the difference of the faces showing up recorded. By taking x and y to represent faces on the tetrahedron and respectively. disrespectively,
- Draw a possibility space to show the possible outcomes. (2marks)
- Find the probability that |x − y| ≥ 3 (1mark)
- The probabilities of three football teams A,B and C winning their first match in CECAFA
championships are 3/5, 7/10 and 2/5 Using a tree diagram, find the probabilitythat:- None of the teams win their first match; (2marks)
- At least two teams win their first match; (3marks)
- At most one team wins its first match. (2marks)
- A fair tetrahedron with faces marked 1,2,3 and 4 and a fair die are tossed together and the difference of the faces showing up recorded. By taking x and y to represent faces on the tetrahedron and respectively. disrespectively,
- The income tax rates in a certain year are as shown below.
Mwenda pays Ksh. 8234 as P.A.Y.E per month. He has a monthly house allowance of Ksh. 10500andisentitled to a personal relief of Ksh. 1162 per month. Determine:Monthly Income (in Ksh.) Tax rate in each shilling (%) 0 - 10164 10 10165 - 19740 15 19741 - 29316 20 29317 - 38892 25 38893 and above 30 -
- his gross tax per month; (2marks)
- his monthly taxable income; (4marks)
- his basic salary per month (2marks)b).
- If the second tax bracket was expanded by 25% Calculate his new P.A.Y.E (2marks)
-
- The table below shows distribution of marks scored by 82 students in a Mathematics test.
Marks 1-10 11-20 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 Frequency (f) 3 5 5 9 11 15 14 8 6 4 - Using an assumed mean of 55.5 calculate
- mean mark (3marks)i
- the standard deviation; (3marks)
- Find the number of students who scored 73% and above (2mark)
- if each students was added 5 marks determine the new mean and the standard deviation (2marks)
- Using an assumed mean of 55.5 calculate
-
- Complete the table below for the equation y = sin x and y = cosx − sinx correct to 2decimal places.(2marks)
xc 0c 1πc
61πc
31πc
22πc
35πc
6πc
7πc
68πc
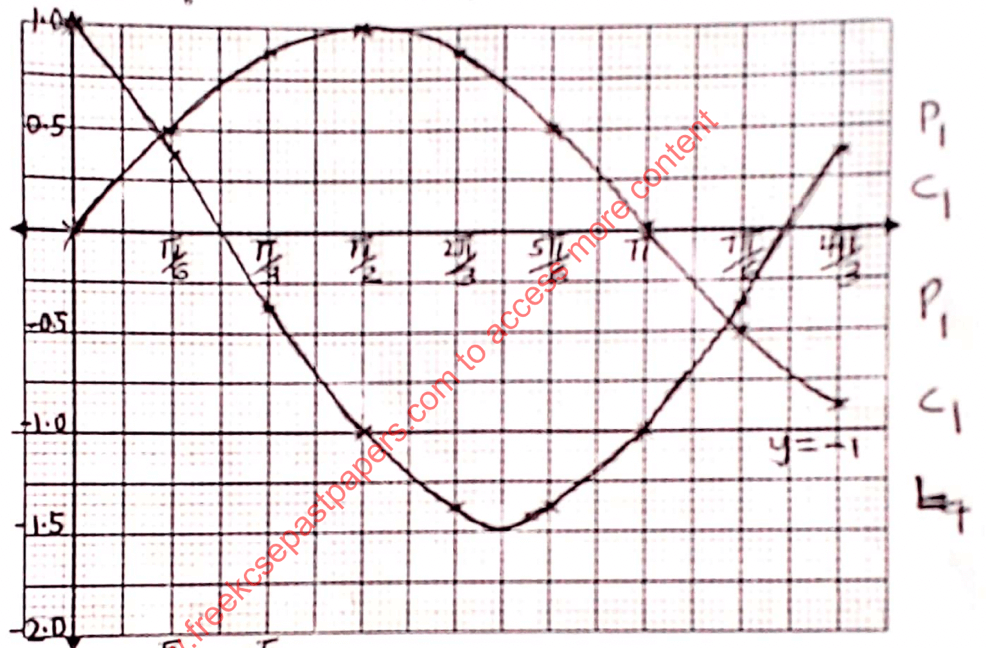
6y = sin x 0.00 0.87 0.50 −0.50 y = cos x − sin x 0.37 −1 −1.37 0.37 - On the graph provided,draw a graph of y = sinx andy = cos x −sinx for 0° ≤ x ≤ 8πc . Use
6
2 cm to represent 1πc on the x-axis and 4 cm to represent 1 unit on the y-axis (4marks)
6
- Use the graph in (b) above to:
- solve the equation cosx= 2 sinx; (2marks)
- find the range of x for which cos x − sin x ≤ −1 (2marks)
- Complete the table below for the equation y = sin x and y = cosx − sinx correct to 2decimal places.(2marks)
- The positions of two points A and B are, A(40°N, 121°W) and B(40°N, 59°E).
- Calculate the distance between A and B along a circle of latitude in nautical miles. (3marks)
- Another point C is on 25°N,59°E An aircraft leaves A at 8.30 amon Sunday and flies to C
through the North Pole at a speed of 200 knots.- Calculate the distance from A to C in nautical miles; (3marks)
- Determine the local time at C when the aircraft left A; (2marks)
- Determine the time and day the aircraft will arrived at C. (2marks)
- Triangle ABC has vertices A(3, -2) B(4, 3) and C(-3, 3). On the grid provided below, draw triangle ABC. (1mark)
- Point A is mapped on to A′(3, 4) by a shear y-axis invariant. On the grid above, drawtriangleA′B′C′ under the shear. (2marks)
- Determine the matrix representing the shear (2marks)
- Triangle A′B′C′ is mapped onto triangle A′′B′′C′′ by the transformation matrix

- State the coordinates of triangle A′′B′′C′′ (2marks)
- Draw triangle A′′B′′C′′ (1mark)
- Find a single matrix that maps triangle A′′B′′C′′ onto triangle ABC (2marks)
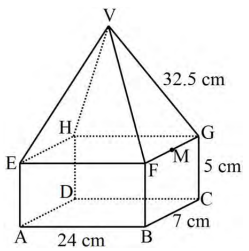
- The figure below represents a model of a cottage with a rectangular base. AB= 24 cm, BC=7cmCG = 5 cm and VG = 32.5 cm . M is the mid – point of FG.
- Calculate correct to 2 decimal places;
- The length AM. (2marks)
- The angle between line EV and AC. (2marks)
- The angle between planes VGF and EFGH. (3marks)
- Calculate the volume of the model. (3marks)
- Calculate correct to 2 decimal places;
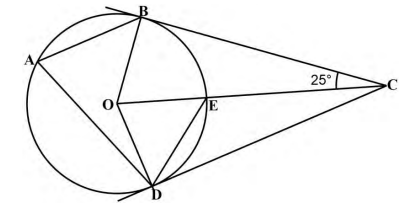
- In the figure below, O is the centre of the circle. BC and DC are tangents to the circle. ∠ = BCO 25°. OEC is a straight line.
Find the value of the following angles, stating the reason in each case:- ∠BOC (2marks)
- ∠OED (2marks)
- ∠CDE (2marks)(iv) ∠BED (2marks)
- Reflex ∠DAE (2marks)
MARKING SCHEME
- a = 11/3 ✓ B1
p = 720 ✓ B1
Phase Angle = 15° ✓ B1 - P = kQ
5√R
3/2 = 9k/2 ✓M1
k = 3/2 × 2/9
= 1/3 ✓M1
p = ¹/₃Q
5√R
P = Q ✓A1
3 5√R - 1836817 = 1,450,000 (1 + r/100 × ¼) ✓M1
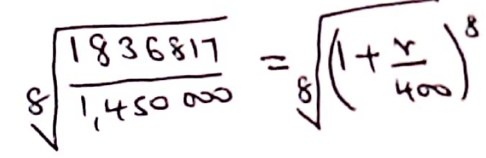
1.0300 = 1 + r/400 ✓M1
0.03 = r/400
r = 12% ✓A1 -
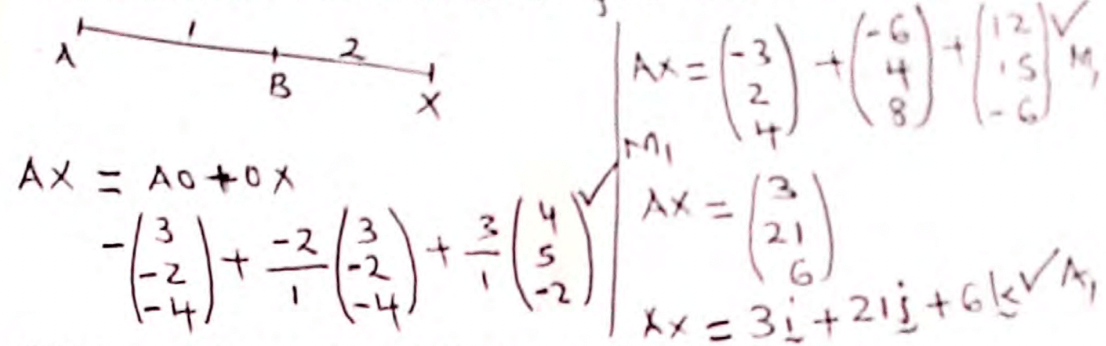
- √52 ✓B1
2 − √3/2
2√52 (4+√3)
(4−√3 (4+√3)
8√52 + 2√156 ✓M1
16 − 3
16√13 + 4√39 ✓A1
13 -
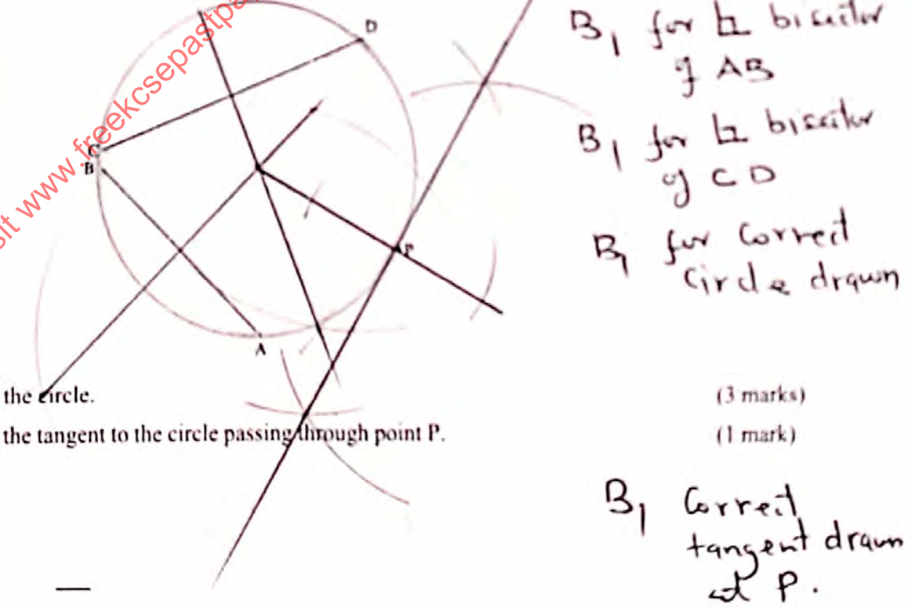
-
- (√3 + √5)4
1 4 6 4 1
(√3)4 (√3)3 (√3)2 (√3)1 (√3)0
(5)0 51 52 53 54
9 + 60√3 + 450 + 500√3 + 625
(9 + 60√3 + 450 + 500√3 + 625) − (9 − 600√3 + 450 − 500√3 + 625) ✓M1
(1084 + 560√3) − (1084 − 560√3) ✓M1
1120√3 ✓A1 -
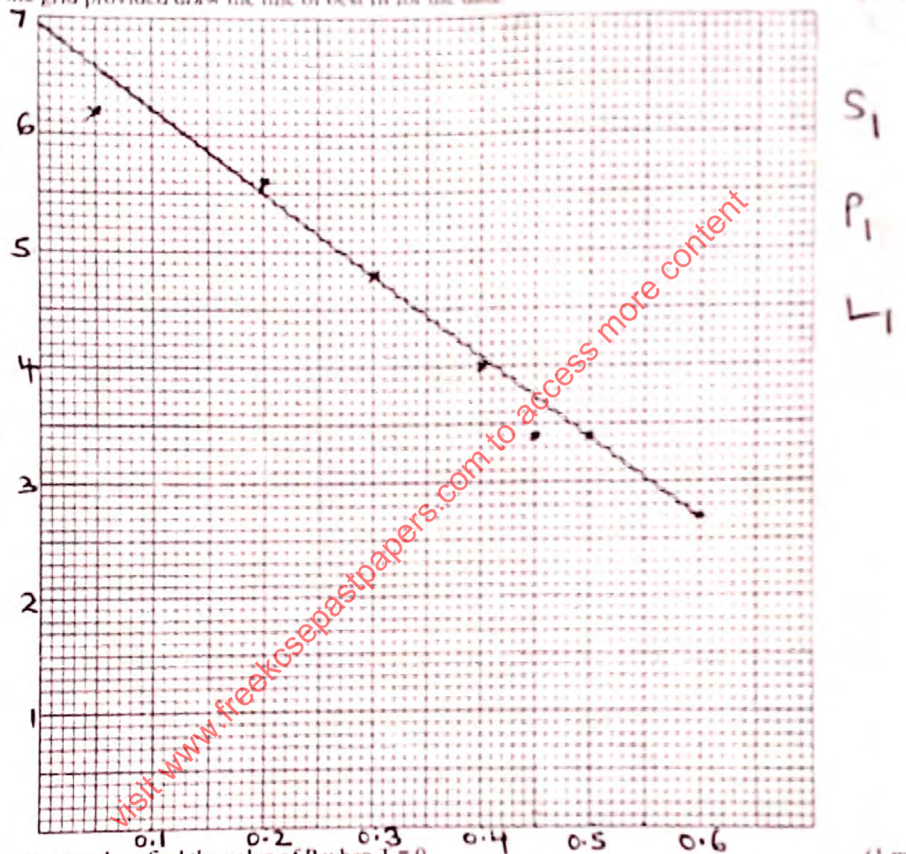
P = 6.9 B1 - Sin2(2x+10) = 3/4
Sin(2x+10) = ± √3/2 ✓M1
2x + 10 = 60, 120, 240, ,300 ✓M1
2x = 50, 110, 230, 290
x = 25°, 55°, 115°, 145°. ✓A1 - d = (x - X̄) : 5 − 2 + 2 + 1 + z −3 − 2 − 4 + 0 = 0
z = −3. ✓B1
x: 18, 11, 15, 14, 10, 10, 11, 9, 13 ✓ B1
Q1 = 10
Q3 = 14+15 = 14.5
2
Quartile deviat = 14.5 − 10 ✓ M1
2
= 2.25 ✓ A1 -
- x + y ≤ 144 ✓B1
- x ≥ 90 ✓B1
- y < 48. ✓B1
- B.P = 100/125 × 182.5
= 146. ✓M1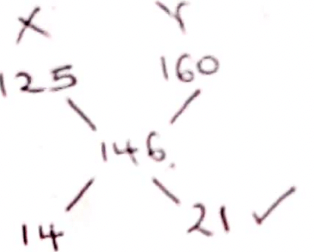 M1
M1
2 : 3 ✓A1 - Truncated value 3640000
% Error = (3645986 − 3640000) × 100%
3645986
5986 × 100%
3645986
= 0.164180553% -
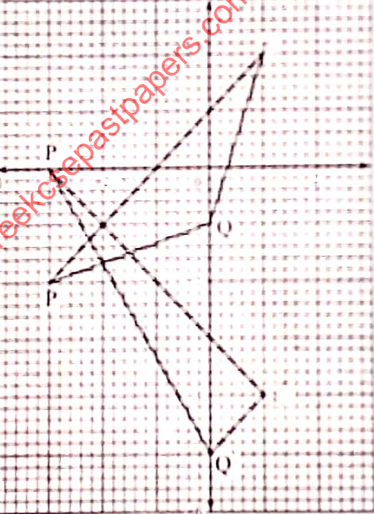
A shear ✓, with the line x= −2 invariant and point P(−3, −2) mapped onto P'(−3, 0) ✓
OR
A shear ✓, with line x = −2 invariant mand shear factor −2✓ - x2 + y2 = 6x − 10y − 18
Centre
2a = 6
a = 3
2b = −10
b = −5
Centre is (3, −5) ✓
Radius : r = √(32 + (−5)2 + 18
= 6.379 or 2√13 -
-
-
X/Y 1 2 3 4 5 6 1 0 −1 −2 −3 −4 −5 2 1 0 −1 −2 −3 −4 3 2 1 0 −1 −2 −3 4 3 2 1 0 −1 −2 - 7/24 B1
-
-
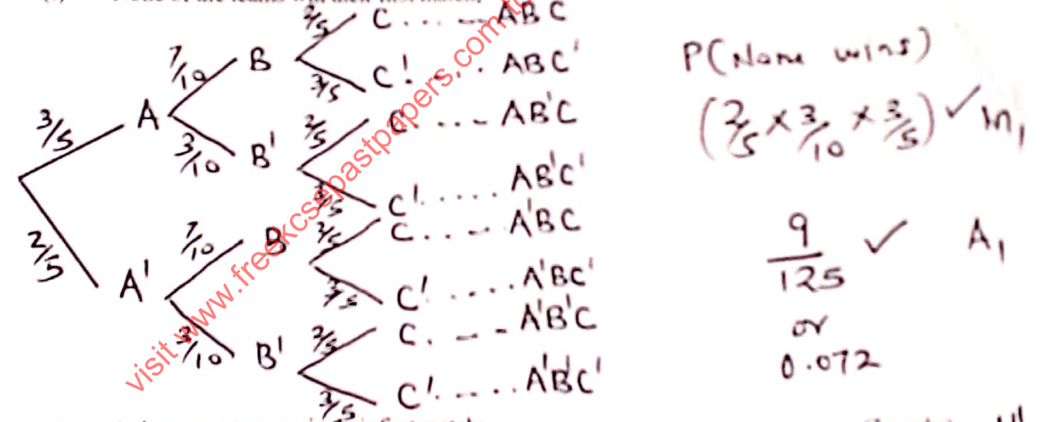
- P(ABC or ABC' or AB'C or A'BC)
(3/5×7/10×2/5) + (3/5×7/10×3/5) + (3/5×3/10×2/5) +(2/5×7/10×2/5) ✓✓M1 M1 All correct probability
151/250 or 0.604 ✓A1 - P(A'B'C' or A'B'C or A'BC' or AB'C')
(2/5×3/10×3/5) + (2/5×3/10×2/5) + (2/5×7/10×3/5) + (3/5×3/10×3/5) ✓
99/250 or 0.396 ✓
ALT
1 − 0.604 = 0.396
-
-
-
- 8234 + 1162✓ = Sh. 9396✓ M1A1
-
1st = 10164 × 0.1 = Sh. 1016.4
2nd = 9576 × 0.15 = Sh. 1436.4 ✓M1
3rd = 9576 × 0.2 = Sh. 1915.2
4th = 9576 × 0.25 = Sh. 2394 ✓M1
5th = x × 0.3 = Sh. 2634
x = 2634
0.3
= 8780/= ✓M1
Taxable income = 1016.4 + 3(9576) + 8780
= Sh. 47672 ✓A1 - 47672 − 10500✓ = Sh. 37172 ✓ M1A1
- 125/100 × 9576 = 11970
1016.4 + (11970 × 0.15) + 1915.2 + 2394 + (6386 × 0.3) ✓M1
= Sh. 9036.9 ✓A1
-
-
Σ = −150Marks 1-10 11-20 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 Frequency (f) 3 5 5 9 11 15 14 8 6 4 X 5.5 15.5 25.5 35.5 45.5 55.5 65.5 75.5 85.5 95.5 d −50 −40 −30 −20 −10 0 10 20 30 40 fd −150 −200 −150 −180 −110 0 140 160 180 160 d2 2500 1600 900 400 100 0 100 400 900 1600 fd2 7500 8000 4500 3600 1100 0 1400 3200 5400 6400 c.f 3 8 13 22 33 48 62 70 76 80
f = 41,100-
- x̄ = 55.5 + (−150/80) ✓B1 for all f.d M1
= 53.625 ✓A1 - S.D =
 B1 for all fd2 M1
B1 for all fd2 M1
= 19.15 ✓A1
- x̄ = 55.5 + (−150/80) ✓B1 for all f.d M1
- 73 = 70.5 + l(n − 62)10✓
8
20 = 10n − 620
n = 63
18 students ✓ - New mean = 58.625 ✓B1
S.D = 19.15 ✓B1
-
-
-
xc 0c 1πc
61πc
31πc
22πc
35πc
6πc
7πc
68πc
6y = sin x 0.00 0.50 0.87 1.00 0.87 0.50 0.00 −0.50 −0.87 y = cos x − sin x 1.00 0.37 −0.37 −1 −1.37 −1.37 −1.00 −0.37 0.37 -
-
- X1 = 3π/20 ± 0.026. B1
or
0.47 ± 0.026
X2 = 69π/60 ± 0.026
or
3.61 ± 0.026 B1 for 90° & 180° - y = −1
πc ≤ x ≤ πc B1 for th range
2
- X1 = 3π/20 ± 0.026. B1
-
-
- D = 60 ∝ cos θ B1 for 180°
= 60 × 180 cos 40 ✓M1
= 8273.28nm ✓A1 -
-
 θ = 115 B1 for 115°
θ = 115 B1 for 115°
60 × 115 ✓ M1
6900nm✓ A1 - 8.30
12.00+
20.30
8.30p.m same day - 6900/200 = 24.5hr
34hrs 30min
2400 10.30
2030 3.30
3.30 7.00
Tuesday 7.00am✓ Tied
-
- D = 60 ∝ cos θ B1 for 180°
-
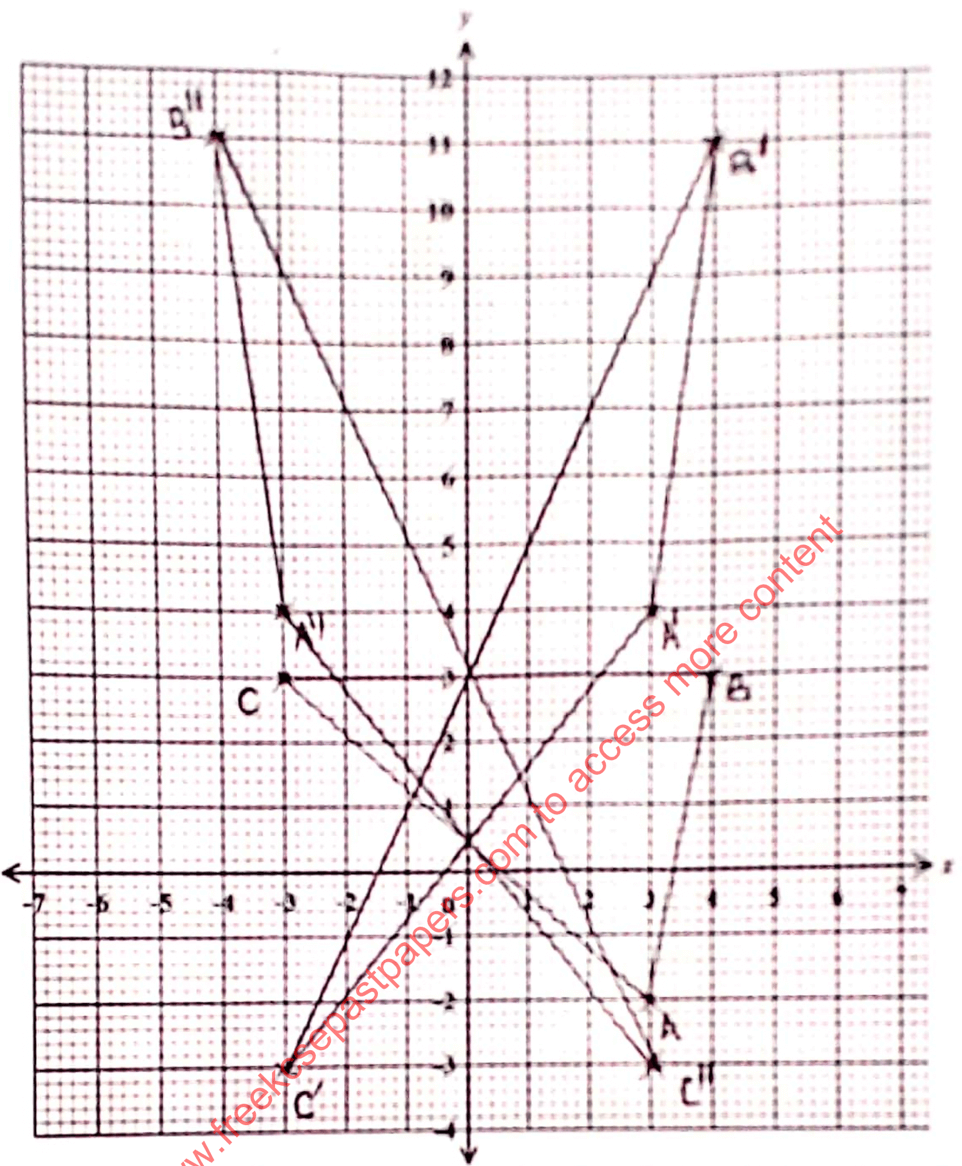
- B1 for correct pts. B and C plortted
B1 complete triangle A'B' - Shear factor = 6/3
= 2 ✓
Matrix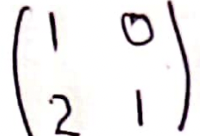 ✓ Follow through
✓ Follow through -
-
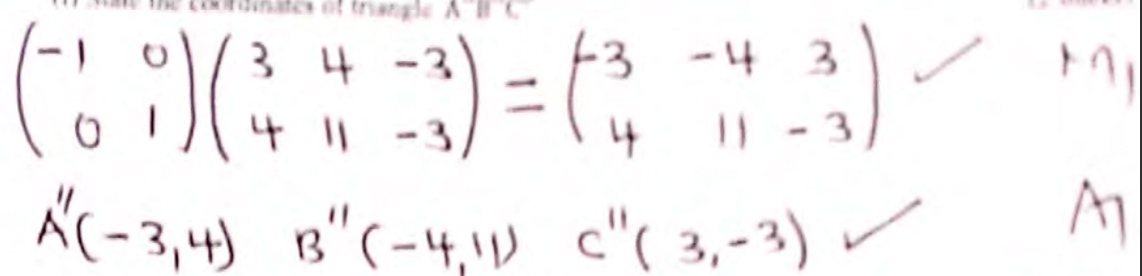
- Draw triangle A''B''C''
-
-
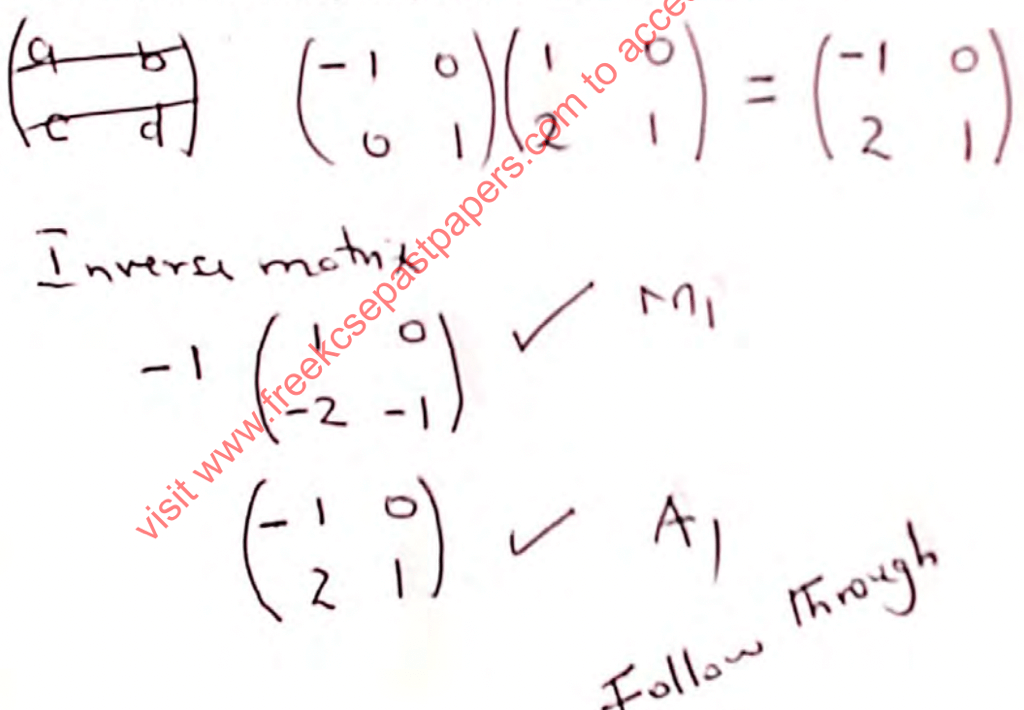
- B1 for correct pts. B and C plortted
-
-
-
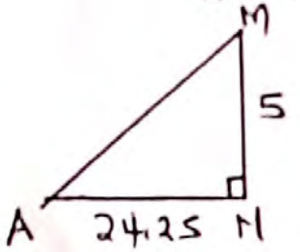
√)(242 + 3.52)
24.24
AM = √(52 + 24.25) ✓M1
= 25.00cm ✓A1 -
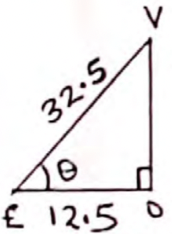
AC = √(72 + 242) = EG
= 25
θ = Cos−1 (12.5/32.5) ✓M1
θ = 67.38° ✓A1 -
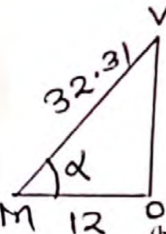
VM = √(32.52 − 3.52)
= 32.31cm ✓B1
∝ = Cos−1 (12/32.31) ✓M1
∝ = 68.20° ✓A1
-
- VO = √(32.312 − 122)
= 29.999 ✓B1
Volume = (24×7×5) + (1/3 ×24×7×29.999) ✓M1
= 2519.94cm3 ✓A1
-
-
- ∠BOC
180 − (90+25) or (90−25)°
65°✓B1 Angle sum of interiror angles in a triangle ✓B1 - ∠OED
∠EDC = (65/2)
= 32.5
∠OED = 180 − (25+32.5)
=122.5° ✓B1 Chord OE subtend 32.5° at circum. equals ∠EDC = 32.5° ✓ B1 - ∠CDE
∠CDE = 65/2
= 32.5° ✓B1 Angle btw a chord and Tangent equal angle subtended by chord on alternate segment. ✓B1 - ∠BED
360 − (2×122.5)
=115° ✓B1 Angles at a point add up to 360° ✓B1 - Reflex ∠DAE
360 − (65/2)
= 327.5. ✓B1 Angle subtended by chord OE at circum. is half angle at centre ✓B1
- ∠BOC
Download Mathematics Paper 2 Questions and Answers - Maranda High Pre Mock Exams 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students