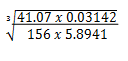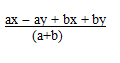MATHEMATICS - Form 2 End of Term 1 2019 Examinations

1. Use logarithm tables to evaluate.                                                                (4mks)
   

2. A straight line passes through points (-2,1) and (6,3) . Find the equation of the line in the from y=mx + c where m and c are constants.                           (3mks)

3. Simplify                              (2mks)
   1.  
      
   2.  
                (2mks)
4. Find the value of x in   (3mks)
   2^x-3 x 8^x+2 =128
5. Two shirts and a pair of trousers cost Ksh240. By buying two pairs of trousers and one shirt Njoroge pays sh300. Find the cost of one shirt and pair of trousers. (4mks)   
                                                                            .   .
6. Convert the recurring decimal into a fraction.   0.321     (3mks)                                                        

7. Three bells ring at intervals of 9 minutes, 15 minutes and 21 minutes. The bells will next ring together at 11.00pm. Find the time the bells had last ring together.   (3 mks)

8. If 5 men can erect 2 cottages in 21 days how many men working at the same rate will be needed to erect 6 cottages in seven days.                                           (2mks)

9. The difference between the exterior angle and interior angle of a regular polygon is 100^0. Determine the number of sides of the polygon.                               (3mks)

10. Find correct to 4 s.f the value of
    ¹/₁₆₃+³/_7.92−²/_2.84 using reciprocal tables.                                       (4mks)

11. Solve for x in    
                                                                                                 (3mks)

12. In a manufacturing firm a radio costs Ksh500 to produce. The cost of materials labour and overheads are in the ratio 7:5:n. If the difference between the cost of materials and labour cost is ksh50 find the cost of overheads. (4mks)

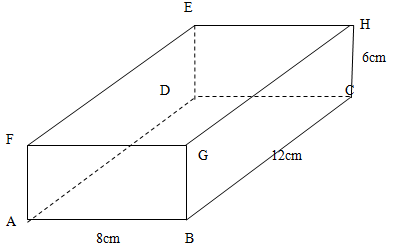
13. The figure below shows a cuboid of length 12cm, width 8cm and height 6cm.
    

       Draw the net of the cuboid and use it to calculate area of the solid.         (4mks)                                  

14. Given that a = -2 and b = 2. What is the value of a^b – b^a.                           (2mks)

15. Find, using tables the value of (0.05317)² (2mks)

16. Simplify without using a calculator.   (2mks)

         2¹/₃ - 1²/₃ ÷⁵/₉ 

SECTION 2 (ANSWER ALL THE QUESTIONS (50 MARKS)

17. A trader sold an item at sh7 500 after allowing his customer15% discount on the marked price of the item. In so doing he made a profit of 35%
    1. Calculate
       1. The marked price of the item.                                                   (3mks)
       2. The price at which the trader had bought the item.                     (2mks)
    2. If the trader had sold the item without giving a discount, calculate the percentage profit he would have made.         (3mks) 
    3. To clear his stock the trader decided to sell the remaining items at a loss of 10%. Calculate the price at which he sold each item.    (2mks)

18. Using a pair of compasses and ruler only
    1. Construct triangle ABC such that AB=7cm, BC=6cm and CA=4cm. (4mks)
    2. Measure and state the size of angle ABC .                                    (1mk)
    3. Drop a perpendicular from point C to line AB. Measure and state the length of this line.     (3mks)
    4. Hence or otherwise, find the area of triangle ABC.                             (2mks)

19.  
    1. On the graph paper draw A(1,2) B(1,5) C(4,6)                                     (1mk)
    2. Draw A¹B¹C¹ the image of ABC after a rotation of 90⁰ anti-clockwise about (0,0).State the coordinates of A¹B¹and C¹.                                         (3mks)
    3. A₁₁B₁₁C₁₁ is the image of A₁B₁C₁ after a reflection on the x-axis. Draw A₁₁B₁₁C₁₁ and state its coordinates.                                                   (3mks)
    4. A¹¹¹B¹¹¹C¹¹¹ is the image of A¹¹B¹¹C¹¹ after a reflection in the line y=x. Draw A¹¹¹B¹¹¹C¹¹¹ and state the coordinates of the vertices. (3mks)
        

20. Measurement of a maize field using a base line XY were recorded in metres as shown below
    
    
    1. Sketch the map of the maize field     (4mks)
    2. Find the area of the field in hectares. (6mks)

21. A line L passes through points (-2, 3) and (-1, 6) and perpendicular to a line P at (-1, 6) .
    1. Find the gradient of line L.   (2mks)
    2. Find the equation of line P in the form ax + by=c where a, b and c are constants.      (3mks)
    3. Given that another line Q is parallel to L and passes through (1,2). Find x and y intercept of Q. (3mks)
    4. Find the point of intersection of line P and Q.                                (2mks)