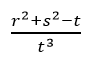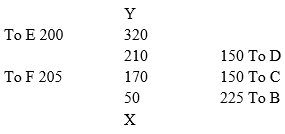Mathematics Questions and Answers - Form 2 Term 3 Opener Exams 2021

Instructions to Candidates

1. This paper has two sections; section A and section B
2. Attempt all the questions in this paper
3. Use of calculators and KNEC mathematical tables may be used except where stated otherwise.

SECTION A

Answer all questions

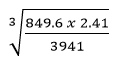
1. Using logarithms tables only, evaluate. (4 Marks)
   
2. Solve the equation (3 Mks)
   x − 2 − 3 − x = x − 2
     3           4           2
3. A tourist arrived in Kenya with sterling pound (€) 4680 all of which he exchanged into Kenyan shillings. He spent ksh. 52,352 while in Kenya and converted the rest of the money into US dollars. Calculate the amount he received in US dollars. The exchange rates were as follows. (3mks
   
   Currency                Buying           Selling
   USṨ                       65.20             69.10
   Sterling pound €     123.40           131.80
4. Solve for the value of x (3 Mks)
   2^3x−2 × 8^x = 4^(x+1)
5. A line passes through the point whose coordinates are A(1,3) and B (-2,-1) find the equation of the line (3 Mrks)
                   _{.    .}
6. Express 1.523 as a fraction. (3mks)
7. Use reciprocal and square tables to evaluate, to 4 significant figures, the expression. . (3Marks)
      1     – 4.151²
   0.3654 
8. The diagonal of a square measures 44cm.Calculate the perimeter of the square. 3mrks
9. Calculate; (3mks)
   2.61 x 21.83 x 0.073
       61.72 x 11.73
10. Patrick spent ²/₅ of his salary on food, ¹/₃ of the remainder on electricity and saved the rest.
    1. What fraction of his salary did he save? (2mrks).
    2. If he spent Sh. 1,200 on food, how much did he spend on electricity? (2Mks)
11. Solve the following simultaneous equation (3 Mks)
    5x+6y=28
    3x+4y=18
12. Two similar containers have base areas of 750 cm2 and 120cm2 respectively. Calculate the volume of the larger container in liters given that the volume of smaller container is 400 cm3 (3 Mrks).
13. If r=5, s=2, and t=3, find the value of; (3mks)
    
14. A farmer has three containers of capacity 12L, 15L and 21L, calculate the capacity of:
    1. The smallest container which can be filled by each one of them an exact number of times (2 Mrks).
    2. The largest container which can fill each one of them an exact number of time.(2 Mks)
15. Given that tan x = ¾, find Cos(90 − x) (2 Mks).
16. The two arms of a pair of compass of dividers are spread so that the angle between them is 450.Find the area of the sector formed if the length of the arm is 8.4cm.Take π = ²²/₇.(3marks)

SECTION II (50 MARKS)

Answer all questions

17. An amount of money was shared among five girls, Alice, Jane, Brenda, Mary and Ivy. Alice got ¹/₈ of the total amount while Jane got ²/₅ of the remainder. The remaining amount was shared equally among Brenda, Mary and Ivy each getting ksh.490.
    1. How much did Jane get? (3mks)
    2. How much was shared among the three girls. (3mks)
    3. Alice, Jane and Ivy invested their money and earned a profit of ksh.3640. a half of the profit was left to maintain the business and the rest shared according to their investments. Calculate how much each got. (4mks)
18. A surveyor recorded the measurements of a field book using xy=400m as the base line as shown below
    
    
    1. Use a scale of 1 cm to represent 50 m to draw the map of the field. (5 Mks)
    2. Find the area of the field in hectares (5 Mks)
19.  
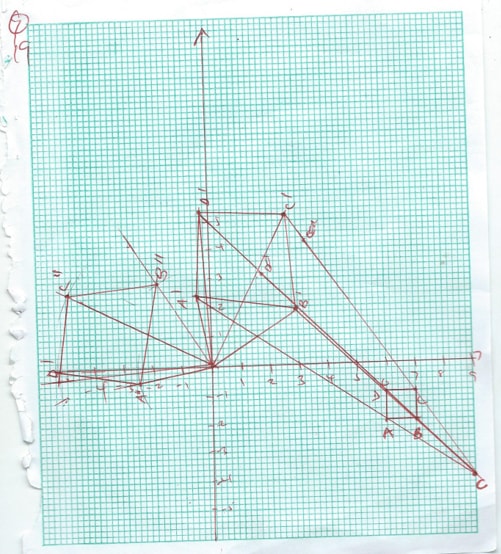
    1. On the grid provided, draw the square whose vertices are A(6,-2) B(7,-2) C(7,-1) and D(6,-1). (2mrks)
    2. 0n the same grid draw;
       1. A’B’C’D’, the image of ABCD under an enlargement scale factor 3centre (9,-4). (4mrks)
       2. A”B”C”D”, the image of A’B’C’D’ under a rotation of +900 about (0,0). (4 mrks)
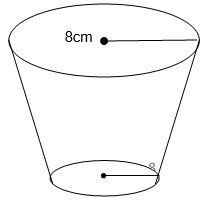
20. A pail is in the shape of a container frustrum with base radius 6cm and top radius 8cm. The slant height of the pail is 30cm as shown below. The pail is full of water.
    
    
    1. Calculate the volume of water in the pail. (6mks)
    2. All the water is poured into a cylindrical container of circular radius 7cm, if the cylinder has the height of 35cm, calculate the height of the cylinder above the water level, which is not in contact with water. (4mks)
21. The sides of a triangular plot of land are 170m, 190m and 210m, but the altitudes of the plot as well as the angles are not known. Find
    1. The area of the plot in Hectares 5mks
    2. The angles of the plot 5mks

Marking Scheme

1.  
2. Multiply by lcm of 3, 4 and 2
   (x − 2) (12)⁴ − (3 − x) (12)³ = (x − 2) (12)⁶
     3                       4                     2
   4x − 8 − 9 + 3x = 6x − 12
   7x − 17 = 6x − 2
   x = 5
3. £ 4650 × 123.40 Ksh = 577512
   spent                        =  52352
   Balance                     = 525, 160
   = 525160 = Us $ 7600
        69.10
   Us dollars = 7600
4. 2^{3x − 2} × 2^3x = 2^(2x+1)
   2^{3x − 2} × 2^3x = 2^2x+2
   2^{3x − 2 + 3x} = 2^2x+2
   6x − 2 = 2x + 2
   4x = 4 
   4      4
   x = 1
5. G = Δy = −1−3 = −4 = 4
          Δx    −2−1    −3    3
   Taking a point A (1,3)
   and point (x,y)
   4 = y − 3 = 4 (x − 1)
   3    x − 1
6. let 1.523523 = r
   1523.523     = 1000r
   
   1000r = 1523.523523
   999r   = 1.523523
   r = 1522 or 1 ⁵²³/₉₉₉
         999
7.     1     − 4.151²
   0.3654
       1     ⇒ 2.737
   0.3654
   4.151² ⇒ 17.23
   2.737 − 17.23
   = −14.494
8. 44² = x²+x²
   44² = 2x²
   1936 = 2x²
     2        2
   x² = 968
   x = 31.11
   P = L+L+L+L
      = 31.11 × 4
      = 124.45 cm
9. 2.61 × 21.83 × 0.073 × 10⁷
        61.72 × 11.73       × 10⁷ 
   = 0.00575 
10. Food = ²/₅
    Electricity = 1 − ²/₅ = ³/₅ × ¹/₃ = ¹/₅
    Saving = 1 − [²/₅ + ¹/₅] = ²/₅
    ²/₅ → 1200
    ¹/₃ → ?
    ¹/₅ × 1200
         ²/₅
11. [5x +6y = 28]3
    [3x + 4y = 18]5
    
    15x + 18y = 84
    15x + 20y = 90
           − 2y = −6
    y = 3
    5x + 18 = 28
    5x = 10
    x = 2 
    y = 3 
    x = 2
12. A.S.F = ⁷⁵⁰/₁₂₀ = ²⁵/₄
    L.S.F = ²⁵/₁₄
    V.S.F = ¹²⁵/₈
     V_{1  = 125}
    400    8
    V₁ = 400 × 125 = 6250
                  8           1000
    = 6.25 litres
13. 5² + 2² − 3 = 25 + 4 − 3
         3³                   27
    = 26
       27
14.  
    1. L.C.M of 12, 15 and 21
       = 420
    2. G.C.D = 12, 15 and 21
       = 3
15. 2 ≥ 3 − x > 5
    2 ≥ 3 − x
    x ≥ 3 − 2 → x ≥ 1
    3 − x > 5
    − x < 5 − 3 → x < 1
    x < 2
    1 ≤ x < 2
16.  
17.  
    1. Alice = ¹/₈
       Jane = ²/₅ of {1 − ¹/₈} = ⁷/₂₀
       {Brenda, Mary, Ivy} → @490 × 3 = 1470 
       = ²¹/₄₀
       ²¹/₄₀ → 1470
       ⁷/₂₀  →
       = 1470 ×⁷/₂₀
               ²¹/₄₀
       
    2. Amount shared
       = 490 × 3
       = 1470
    3. Alice amount = ¹/₈ × 2800 = 350
       Ivy                                   = 490
       Jane                                 = 980
                                                1820
       Profit shared = ³⁶⁴⁰/₂ = 1820
       Alice =  350 × 1820 = 350
                  1820
       Jane = 980 × 1820 = 980
                 1820
       Ivy =  490   × 1820 = 490
                1820
18.  
    1.   
       
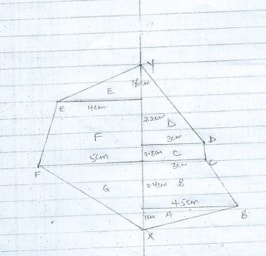
    2. A - Right angled Δ A = ¹/₂bh = ¹/₂ × 1 × 4.5 = 2.25 cm²
       B - Trapezium = ¹/₂(a+b)h = ¹/₂(3 + 4.5)2.4 = 9cm²
       C - Rectangle = L × W = 0.8 × 3 = 2.4 cm²
       D - Right angled Δ A = ¹/₂bh = ¹/₂ × 3 × 3.8 = 5.7 cm²
       E - Right angled Δ A = ¹/₂bh = ¹/₂ × 1.6 × 4 = 3.2 cm²
       F - Trapezium = ¹/₂(a+b)h = ¹/₂(5 + 4)3 = 13.5cm²
       G - Right angled Δ = ¹/₂ × 3.4 × 5 = 8 cm²
       total area = 44.55 cm²
       1 cm rep 50 m
       1 cm² rep 2500 m² 
       11135 m² = 11.1375 ha
       10,000
19.  
     
20.  
    1. 8 = 30 + x
       6         x
       8x = 180 + 6x
       2x = 180
       x = 90 cm
       h² = 90² − 6²
       h = 89.80 cm
       H² = 120² − 8²
       H = √(400 − 64)
       H = 119.75cm
       V₁ = ¹/₃ × ²²/₇ × 8 × 8 × 119.75 = 8027.61
       V₂ = ¹/₃ × ²²/₇ × 6 × 6 × 89.80 = 3386.74
       Volume of the frustrum = V₁ − V₂
       = 8027.61 − 3386.74
       = 4640.87 cm³
    2. V = 4640.87
       V of the cylinder = πr²h
       ²²/₇ × 7 × 7 × h = 4640.87 cm²
       h = 4640.87 = 30.14cm
                154
       height above the water level
       = 35cm − 30.14 cm
       = 4.86 cm
21.  
    1. A = √(S(s−a)(s−b)(s−c))
       s = ¹/₂ [170 + 190 + 210]
        = 285
       A = √(285(285−210)(285−190)(285−170)
       A = √(285 (75)(95)(115)
       A = √233521875
       = 15,281.4225 m²
              10000
       = 1.528 ha
    2. A = ¹/₂ab sin C
       sin C = Area = 15281.42
                  ¹/₂ab     ¹/₂×210×190
       sin C = 0.76598
       ∠ C = 49.99^o
       sin B = Area
                 ¹/₂ac
       15281.42
       ¹/₂ × 210 × 170
       = ∠ 58.88^o
       ∠ A = (180 − (49.99+58.88))
       = 71.13^o