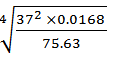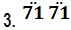Mathematics Questions and Answers - Form 2 Term 1 Mid Term Exams

MATHEMATICS
FORM 2
MID TERM
TERM 1

INSTRUCTIONS

• Answer all the questions

SECTION A

1. Evaluate -8÷2+12x9-4x6  [3 Marks]
                   56÷7x2           
2. A matatu travelling at 56 Km/h take 2 ½ hours to move from town A to town B.
   Find the distance between towns A and B. [2 Marks]
3. Determine the gradient and the co-ordinates of the (x) and (y) intercepts of the line whose equation is [3 Marks]
   2y+3x=1
4. Find the correct 3s.f the value of [2 Marks]
   ¹/_6.43 + ²/_3.56 + ¹/_8.51
5. Without using mathematical tables, evaluate [3 Marks]
   27^2/₃ x (⁸¹/₁₆)^-1/₄
6. The diagonals of a rhombus measure 9.2 cm and 7.5 cm respectively. Calculate the area of the rhombus [2 Marks]
7. A man is three times as old as his daughter. In twelve years time he will be twice as old as his daughter. Find their present age. [3 Marks]
8. Use logarithm tables to evaluate [4 Marks]
   
9. An artisan has 63Kg of metal of density 7000Kg/m³. He intends to use it to make a rectangular pipe with external dimension 12 cm by 15 cm and internal dimension 10 cm by 12 cm. calculate the length of the pipe in metres. [4 Marks]
10. Determine the equation of a line that passes through (-2,5) and is parallel to the line whose equation is [4 Marks] 5y+2x=10
11. Use the elimination method to solve the simultaneous equations[4 Marks]
    2x+3y=1
    3x=2y+8
12. A trader sold a wrist watch for sh. 3,150 after giving a 10% discount. Find the marked price of the watch. [2 Marks]
13. Express as a fraction in its lowest form [3 Marks]
    
14. Seven people can build five huts in 30 days. Find the number of people working at the same rate that will build nine similar huts in 27 days. [3 Marks]
15. The size of each interior angle of a regular polygon is five times the size of the exterior angle. Find the number of sides of the polygon. [3 Marks]
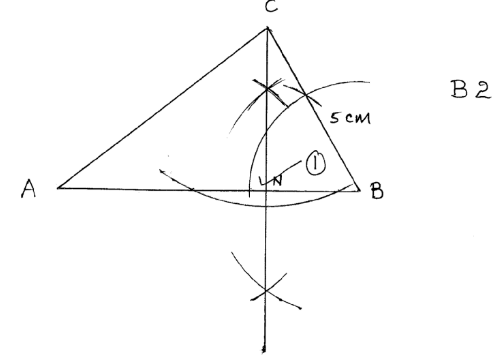
16. Line AB below shows a side of triangle ABC. BC= 5cm and angle ABC = 60º
    
    
    1. Using a ruler and compass only, complete the triangle ABC. [2 Marks]
    2. From C construct a perpendicular to meet line AB at point N. Measure length CN in centimetres [2 Marks]
    3. Determine the area of triangle ABC [1 Mark]

SECTION B [50 MARKS]

17.           
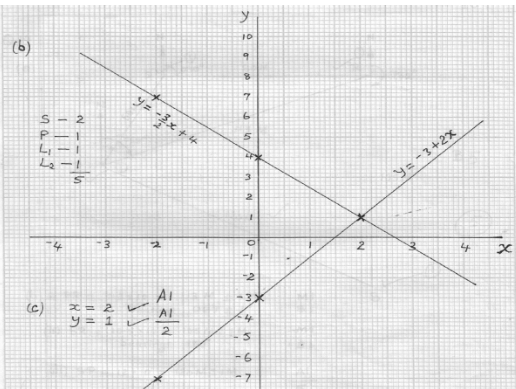
    1. Complete the tables below for the equations of the lines y-³/_4x+4 and y=-3+2x
       

       x	-2	0	2
       y		4

       
       

       x	-2	0	2
       y		-3

       
       
       
    2. using one big square to represent 1 unit on y – axis and 2 big squares to represent 1 unit on – axis, draw the lines + 4 and [5 Marks]
    3. use your graphs to solve the simultaneous equations[1 Mark]
       3x+2y=8
       2x-y=3
18. a school hall measure 10m long, 7m wide and 4m high. All its inside walls and ceiling are painted.
    Calculate,
    1. the total surface area painted
    2. the cost of painting at 200/= per square metre. [10 Marks]
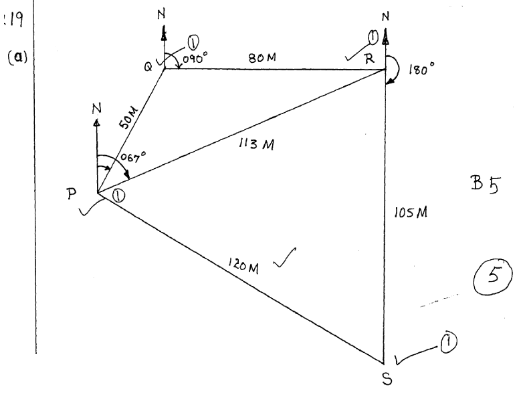
19. a bird flies from tree P to another tree Q which is 50m on a bearing of 030º from P. from Q the bird flies 80m due west to another tree R and finally flies due south to another tree S which is on a bearing of 120º from P.
    1. using the scale 1cm = 10m, construct an accurate scale drawing showing the positions of P,Q,R, and S [5 Marks]
    2. by measurement from your scale drawing determine;
       1. the distance and bearing of R from Q [2 Marks]
       2. the distance and bearing of S from R [2 Marks]
       3. the distance of S from P [1 Mark]
20.    
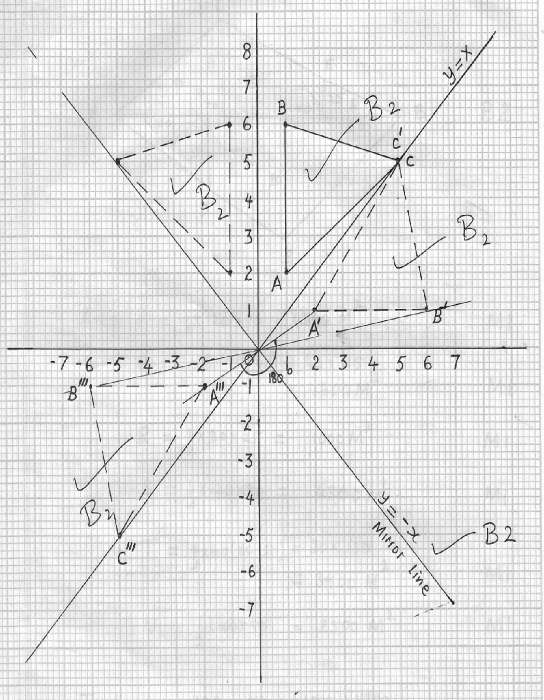
    1. On a Cartesian plane plot and draw the triangle ABC, A(1,2), B (1,6), C (5,5) [2 Marks ]
    2. Draw the image of triangle ABC after reflection on the line y=x
    3. Draw A"B"C" the image of ABC after reflection along y – axis [2 Marks]
    4. Draw A"B"C" the image of A'B'C' after rotation through -180 about the origin [2 Marks]
    5. Determine the mirror line that makes A'''B"'C"' the image of triangle ABC [2 Marks]
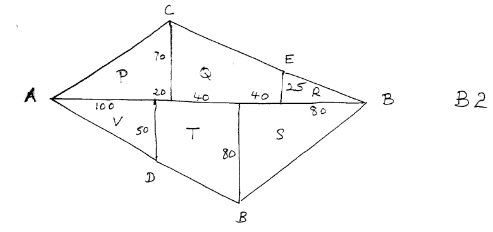
21. The table shows recordings from surveyors’ field book.
    
    1. Draw a sketch diagram from the data in the field book [2 Marks]
    2. Given that the recordings are in metres, determine the area of the land in hectares.[8 Marks]

MARKING SCHEME

SECTION A

1. Evaluate -8÷2+12x9-4x6 [3 Marks]
                      56÷7x2   
   -8÷2+12X9-4x6 = -4+108-24=80
   56÷7x2= 8x2=16
   ⁸⁰/₁₆=5
          
2. A matatu travelling at 56 Km/h take 2 ½ hours to move from town A to town B.
   Find the distance between towns A and B. [2 Marks]
   Distance= Speed x time
   56 x ⁵/₂=140km/h
   
   
3. Determine the gradient and the co-ordinates of the (x) and (y) intercepts of the line whose equation is [3 Marks]
   2y+3x=1
   y=¹/₂ - ³/₂x
   Gradient= -³/₂
   when y=0, x=¹/₃ 
   (0, ¹/₃)
   when x=0, y=¹/₂
   (0,¹/₂)
   
   
4. Find the correct 3s.f the value of [2 Marks]
   ¹/_6.43 + ²/_3.56 + ¹/_8.51
   0.1555+(0.2809x2)+0.1175
   0.1555+0.5618+0.1175
   0.8348 
   0.835
   
   
5. Without using mathematical tables, evaluate [3 Marks]
   27^2/₃ x (⁸¹/₁₆)^-1/₄ 
   (3³)^2/₃ x (³⁴/2⁴)^-1/4
      3²x(²⁴/3⁴)^1/4
   =3²x²/₃ = 3x2
   =6
   
   
6. The diagonals of a rhombus measure 9.2 cm and 7.5 cm respectively. Calculate the area of the rhombus [2 Marks]
   ½ x 9.2 x 7.5=34.5cm²
   
7. A man is three times as old as his daughter. In twelve years time he will be twice as old as his daughter. Find their present age. [3 Marks]
   Daughter's age=x
   Man's age =3x
   3x+12=2(x+12)
   3x+12=2x+24
   3x-2x=24-12
   x=12
   12x3=36 years
   
   
8. Use logarithm tables to evaluate [4 Marks]
   
   
   
9. An artisan has 63Kg of metal of density 7000Kg/m³. He intends to use it to make a rectangular pipe with external dimension 12 cm by 15 cm and internal dimension 10 cm by 12 cm. calculate the length of the pipe in metres. [4 Marks]
   Density=m/v
   Volume=m/d = ⁶³/₇₀₀₀=0.009m³=9000cm³
   Volume = l x w x h= 12x15=180cm² 
   10x12=120cm²
   180cm²-120cm²=60cm^{2
   9000}/₆₀=150cm=1.5m
   
   
10. Determine the equation of a line that passes through (-2,5) and is parallel to the line whose equation is [4 Marks] 5y+2x=10
    5y=10-2x
    y=2 - ²/₅x
    m1=-2/5
    y=mx+c
    5=-2/5x-2 +c
    5=4/5+c
    41/5=c
    y-5  =-2
    x+2    5
    5y-25=-2x-4
    5y=-2x-21
    
    
11. Use the elimination method to solve the simultaneous equations[4 Marks]
    2x+3y=1
    3x=2y+8
    (3x -2y=8)x2
    (2x+3y=1)x3
    6x-4y=16
    6x+9y=3
    -13y=13
    y=-1
    3x-2(-1)=8
    3x+2=8
    3x=6
    x=2
    
12. A trader sold a wrist watch for sh. 3,150 after giving a 10% discount. Find the marked price of the watch. [2 Marks]
    3150=90%
       ?  =100%
    ¹⁰⁰/₉₀x3150=3500
    Marked Price= Ksh.3500
    
    
13. Express as a fraction in its lowest form [3 Marks]
    
    3.71717171...=r
    37.171717....=10r
    371.717171..=100r
    100r-r=99r
    99r=368
    =3 ⁷¹/₉₉
    
    
14. Seven people can build five huts in 30 days. Find the number of people working at the same rate that will build nine similar huts in 27 days. [3 Marks]
    7 people→ 5 huts →30 days
        ?      → 9 huts →27days
    Rater of work is same
    ³⁰/₂₇ x ⁹/₅ x7=
    2x7=14
    14 people
    
    
15. The size of each interior angle of a regular polygon is five times the size of the exterior angle. Find the number of sides of the polygon. [3 Marks]
    interior angle=5x
    exterior= x
    5x+x=180
    6x=180
    x=30
    360/30=12
    12 sides
    
    
16. Line AB below shows a side of triangle ABC. BC= 5cm and angle ABC = 60º
    
    
    1. Using a ruler and compass only, complete the triangle ABC. [2 Marks]
    2. From C construct a perpendicular to meet line AB at point N. Measure length CN in centimetres [2 Marks]
       
    3. Determine the area of triangle ABC [1 Mark]
       ¹/₂ x 8 x 5
       =20cm²

SECTION B [50 MARKS]

17.           
    1. Complete the tables below for the equations of the lines y-³/_4x+4 and y=-3+2x
       

       x	-2	0	2
       y	7	4	1

       
       

       x	-2	0	2
       y	-7	-3	1

    2. using one big square to represent 1 unit on y – axis and 2 big squares to represent 1 unit on – axis, draw the lines + 4 and [5 Marks]
    3. use your graphs to solve the simultaneous equations[1 Mark]
       3x+2y=8
       2x-y=3
       
18. a school hall measure 10m long, 7m wide and 4m high. All its inside walls and ceiling are painted.
    Calculate,
    1. the total surface area painted
       Area of  ceiling(10x7)=70cm²
       Area of walls(7x4)2=56cm²
       Area 0f walls(10x4)2=80cm²
       Total surface areas= 70+56+80=206cm²
       
       
    2. the cost of painting at 200/= per square metre. [10 Marks]
       cost of painting=206x200=41,200
       
       
19. a bird flies from tree P to another tree Q which is 50m on a bearing of 030º from P. from Q the bird flies 80m due west to another tree R and finally flies due south to another tree S which is on a bearing of 120º from P.
    1. using the scale 1cm = 10m, construct an accurate scale drawing showing the positions of P,Q,R, and S [5 Marks]
       
    2. by measurement from your scale drawing determine;
       1. the distance and bearing of R from Q [2 Marks]
          11.3 x 10=113m±1
          
          
       2. the distance and bearing of S from R [2 Marks]
          Bearing 067±1
          
          
       3. the distance of S from P [1 Mark]
          Bearing 180º
20.    
    1. On a Cartesian plane plot and draw the triangle ABC, A(1,2), B (1,6), C (5,5) [2 Marks ]
    2. Draw the image of triangle ABC after reflection on the line y=x
    3. Draw A"B"C" the image of ABC after reflection along y – axis [2 Marks]
    4. Draw A"B"C" the image of A'B'C' after rotation through -180 about the origin [2 Marks]
    5. Determine the mirror line that makes A'''B"'C"' the image of triangle ABC [2 Marks]
       
21. The table shows recordings from surveyors’ field book.
    
    
    1. Draw a sketch diagram from the data in the field book [2 Marks]
       
    2. Given that the recordings are in metres, determine the area of the land in hectares.[8 Marks]
       P=½x120x70=4200m²
       Q=½x80(75+40)=40x15=4600m²
       R=½x80x25=100m²
       S=½x120x80=4800m²
       T=½x60(80+50)=30x130=3900cm²
       V=½x100x50=2500m²
       Total area=4200+4600+1000+4800+3900+2500=21000m²
       =2.1ha