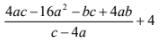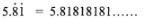Mathematics Questions and Answers - Form 2 Mid Term 2 Exams 2021

Instructions to candidates.

The paper contain two sections: Section I and section II.
Answer All the questions in section I and strictly any five questions from section II.
All answers and working must be written in the question paper in the spaces provided below each question.
Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except unless stated otherwise.

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided

Simplify: (3 marks)
A plot in the shape of a rectangle measures 608 m by 264 m. Equidistant fencing posts are placed along its length and breadth as far apart as possible. Find:
1. The distance between the posts (2 marks)
2. The number of posts used (2 marks)
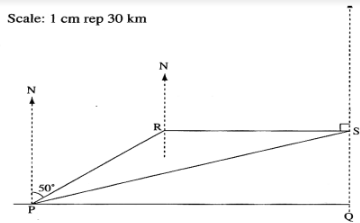
A ship P of 180 km West of a port Q. Another ship R is at a distance of 90 km and on a bearing of 050° from P. A third ship S is due East of R and due north of Q. By scale drawing determine the bearing of S from P. (Use a scale of 1 cm for 30 km) (4 marks)
Simplify the following by use of common factors: (3 marks)
A business woman bought 288 bananas at sh 10 for every 12. She sold all of them at sh 20 for every 18. What was her percentage profit? (4 marks)
Solve the simultaneous equations (3 marks)
3x − 2y = 7
5x + y = 3
When a piece of cloth was washed, it shrank. Its length decreased from 150 cm to 120 cm.
1. In what ratio did it decrease? (1 mark)
2. Suppose the width decreased in the same ratio. What is the new width if the original width was l.4 m? (2 marks)
Given the following currency exchange rate, calculate to 3 significant figures the number of dollars that can be exchanged for 25 Sterling pounds. (3 marks)
1 US dollar ($) = Ksh 76.85
1 Sterling pound (£) = Ksh 115.30 (3 marks)
A cylindrical tank whose diameter is 1.4 metres and height 80 cm is initially empty. Water whose volume is 492.8 litres is poured into the tank. Determine the fraction of the tank filled with water. (Take π = ²²/₇ (4 marks)
A man is now three times as old as his daughter. In twelve years time he will be twice as old as his daughter. Find their present ages. (3 marks)
The number .5 81..contains an integral part and a recurring decimal. Convert the number into an improper fraction and hence into a mixed number. (3 marks)
An article which is marked for sh 450 is sold to a customer for sh 393.75. What percentage discount is the customer allowed? (3 marks)
On a certain map a road 20 km long is represented by a line 4 cm long. Find the area in hectares of a ranch represented by a rectangle measuring 2.8 cm by 1.6 cm on this map. (3 marks)
Syengo spends one-third of his salary on food, one-quarter on rent, three-fifths of the remainder on transport and saves the rest. If he spends sh 1 800 on transport, find how much money he saves. (3 marks)
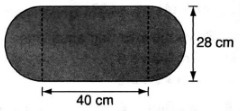
The base of an open vessel is as shown in the figure below. The curved ends are semicircular and the height of the vessel is 18 cm.

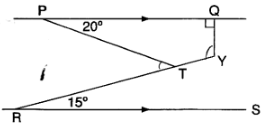
Calculate the area of metal sheeting required to construct the vessel, allowing 10% for wastage. (4 marks)
In the figure below PQ is parallel to RS. Angle QPT = 20º, angle TRS = 15°, angle PQY = 90°, RTY is a straight line.

Calculate:
1. acute angle PTR
2. Angle QYT

SECTION II (50 marks)
Answer any five questions in this section in the spaces provided.

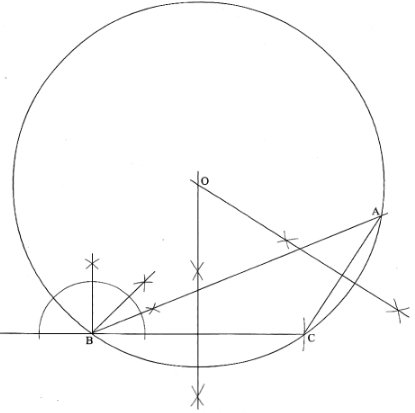
1. Using a ruler and a pair of compasses only, construct triangle ABC in which BC 6 cm, _AB = 8.8 cm and angle ABC 22 ½°. (4 marks)
2. Measure AC and angle ACB. (2 marks)
3. Construct a circle that passes through A, B and C. (3 marks)
4. What is the radius of this circle? (1 mark)
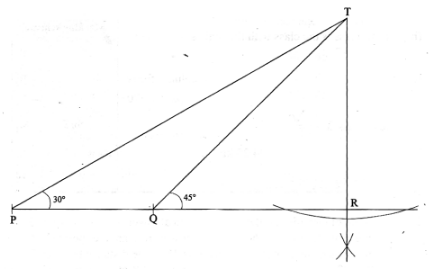
1. The angle of elevation of the top of a vertical tower from a point P is 30°. The angle of elevation of the top of the tower from another point Q which is nearer the foot R of the tower is 45°. The distance between P and Q is 20 metres and the points P, Q and R are on the same straight line on level ground. Using a scale of 1 cm to represent 5 m, draw an accurate scale drawing to represent the above information. (4 marks)
2. Use your scale drawing to determine
  1. the height of the tower (2 marks)
  2. the distance QR (2 marks)
  3. the distance PR (2 marks)
1. A Jua Kali artisan made an article and sold it to a wholesaler at a profit of 20%. The wholesaler sold the article to a retailer at a profit of 30%. The retailer finally sold the article to a customer at a profit of 50%.
  If it cost the artisan sh 500 to make the article, find how much the customer paid for it. (3 marks)
2. A customer paid sh 1 560 for another article. Determine how much the wholesaler had paid for it. (3 marks)
3. During a clearance sale the retailer reduced his prices by 10%. Find the percentage profit the retailer _made on an article which had cost the artisan sh 1 000 to make (4 marks)
1. A newly built classroom measuring 6.3 m long, 4.5 m wide and 3.2 in high is to be cemented on the floor and all inside walls. The classroom has one door measuring 1.85 m by 80 cm and four windows measuring 1.5 m by 70 cm each. Cementing materials cost sh 500 per square metre while labour costs 20% of the cost of cementing materials. Calculate to one decimal place, the total surface area to be cemented. (5 marks)
2. the cost of cementing materials. (2 marks)
3. the total cost of cementing the classroom. (3 marks)

A train left Mombasa on Monday evening and travelled to Kisumu according to the travel time table below. The train arrived in Kisumu on Wednesday morning of the same week.

Mombasa	dep.	1930h
Mtito Andei	arr.	0250h
Mtito Andei	dep.	0335h
Nairobi	arr.	1050h
Nairobi	dep.	1240h
Nakuru	arr.	1900h
Nakuru	dep.	2015h
Kisumu	arr.	0900h

Determine the time the train took to travel between
1. Mombasa and Mtito Andei
2. Mtito Andei and Nairobi
3. Nairobi and Nakuru
4. Nakuru and Kisumu (4 marks)
Calculate the total time for the whole journey. (4 marks)
Given that the railway road distance between Mombasa and Kisumu is 1 200 km, calculate the avenge speed for the whole journey. (2 marks)

A rectangular sheet measuring 80 cm by 50 cm is 2 mm thick and is made of metal whose density is 2.5 g/cm³. A square of side 5 cm is removed from each corner of the rectangle and the remaining part folded to form an open cuboid.
1. Calculate
  1. the area of metal which forms the cuboid. (2 marks)
  2. the mass of the empty cuboid in kilograms. (4 marks)
2. The cuboid is filled with water whose density is 1 g/cm³. Calculate the mass of the cuboid when full of water. (4 marks)
1. Copy and complete the tables (i) and (ii) below for the functions y = 7 − 3x and y= 2x − 8 respectively
  1. y = 7 – 3x
    
    x −2 −1 0 1 2 3 4 5
    
    y 13 7 −8
  2. y = 2x − 8
    
    x −4 −2 0 2 4 6 8 10
    
    y −16 −8 4
2. On squared paper and on the same grid draw the graph of y = 2x - 8 and y = 7 – 3x (4 marks)
3. What is the nature of the two graphs you have drawn? (1 mark)
4. Use your graphs to solve the simultaneous equations. (1 mark)
  3x + y = 7
  2x − y = 8
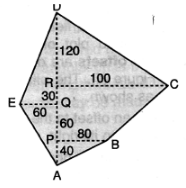
The table below represent a surveyor’s a field –book record for a piece of land.

Metres to D

250

130 90 to C

To E 60 100

40 80 to B

From A

Calculate the area of the field in hectares. (10 marks)

MARKING SCHEME

Numerator = ⁴/₅ (2 + ¼ − ³/₈) ÷ (⁵/₂ × ³/₁₆)
= ⁴/₅ × 1⁷/₈ ÷ ¹⁵/₃₂
= ⁴/₅ × ¹⁵/₈ × ³²/₁₅ = ¹⁶/₅
Denominator = ³/₅ × ¹⁶/₅ = ⁴⁸/₂₅
Expression = ¹⁶/₅ ÷ ⁴⁸/₂₅ = ¹⁶/₅ × ²⁵/₄₈ = ⁵/₃ = 1²/₃ (3 marks)
1. Distance between posts is the HCF of 608 and 264 (2 marks)
  608 = 2 × 2 × 2 × 2 × 2 × 19
  264 = 2 × 2 × 2 × 3 × 11
  HCF= 2³ = 8
  Distance between posts = 8m
2. Number of posts = 2(l + b)
  8
  =2(608 + 264)
  8
  = 1744 = 218
  8 (2 marks)
Bearing of S from P72° (4 marks)
= 4a(c−4a) − b(c−4a) +4
c−4a
=(4a−b)(c−4a) +4
c−4a
=4a−b+4 (3 marks)
Buying price (BP) = 288 × 10 =Sh 240
12
Selling price (SP) = 288 =Sh 320
18
Percentage profit = SP − BP × 100
BP
= 320 − 240 × 100
240
=33¹/₃% (4 marks)
3x − 2y = 7 ..........(i) ( mult.eqn (i) by 1
5x + y = 3 ..........(ii) and eqn. (ii) by 2
⇒3x − 2y = 7
10x + 2 = 6
13x = 13
x=1
Subst. for x in eqn. (ii)
5 × 1 + y = 3
y = 3 − 5
= −2
Hence x = 1, y= −2 (3 marks)
1. In what ratio did it decrease? (1 mark)
  120 :150 ⇒ 5:4
2. new width = ⁴/₅ × 140cm
  = 112cm or 1.12m (2 marks)
Given the following currency exchange rate, calculate to 3 significant figures the number of dollars that can be exchanged for 25 Sterling pounds.
1 US dollar ($) = Ksh 76.85
1 Sterling pound (£) = Ksh 115.30
Convert sterling pounds into Kenya shillings
25 Sterling pounds = Kshs 25 × 115.30
Now convert Ksh. into dollars = 25 × 115.30
76.85
=$ 37.5
Volume of tank = πr²h where r = 70cm, h = 80cm
= ²²/₇ × 70 ×70 × 80 litres
1000
= 1232litres
Fraction filled = 492.8
1232
= 4928
12320
= ²/₅ (4 marks)
Let daughters age be y years ⇒ man's age is 3y years.
In 12 years time: duaghter will be (y+ 12) yeras old
and man will be (3y+ 12 ) years old
∴ 3y + 12 = 2(y + 12)
3y + 12 = 2y + 24
3y − 2y = 24 − 12 ⇒ y = 12
Hence daughter's age is 12 years and man's age is 36years (3 marks)
Let r = 5.81818181.........(i)
then 100 r = 581.818181.........(ii)
Subtract eqn (i) from eqn. (ii)
99r = 576
r= 576
99
= ⁶⁴/₁₁ or 5⁹/₁₁ (3 marks)
Marked Price (MP) = sh. 450
Selling Price (SP) = sh. 393.75
% discount = MP − SP × 100
MP
=450 − 393.75 × 100
450
= 56.25 × 100
450
= 12.5%
4cm on map represents 20km
1cm on map represents 5km = 5000m
2.8cm on map rep 2.8 × 5000 = 14000m
1.6cm on map rep. 1.6 × 5000 = 8000m
∴ Area of ranch = 14000 × 8000m²
= 14000 × 8000
10⁴
=11200ha (3 marks)
Fraction spent on food and rent = ¹/₃ + ¼ = 4+3 = 7
12 12
Remainder = 1 − ⁷/₁₂ = ⁵/₁₂
Fraction spent on transport = ³/₅ of ⁵/₁₂ = ³/₅ × ⁵/₁₂ =¼
Fraction saved = ⁵/₁₂ − ¼ = 5 − 3 = ²/₁₂ or ¹/₆
∴ ¼ of salary = sh.1800
¹/₆ = ?
1800 × ¹/₆ × ⁴/₁= 1200
=Kshs. 1200 (3 marks)
base area = ²²/₇ × 14 × 14 × ½ × 2 +40 × 28 = 1736cm²
Curved surface area = (²²/₇ × 28 × ½ + 40 + ²²/₇ × 28 × ½ + 40) × 30 (4 marks)
=5040cm²
total area = 1736 + 5040 + 1736 = 8512cm²
Metal needed = 110 × 8512 = 9363.2cm²
100
1. Angle PTR = 15 + 20 = 35º
2. ∠20 + 90 + ∠QYT + (180 − 35) = 360
  ∠QYT = 105°
2. AC = 4.1cm ± 0.1cm
  ∠ACB = 122 ± 1°
4. radius = 5.2 ± 0.1cm
2. 1. Height TR = 5.5 × 5 = 27.5 ± 0.5m (2 marks)
  2. Distance OR = 5.5 × 5 = 27.5 ± 0.5m (2 marks)
  3. The distance PR = 11 × 5 = 55 ± 0.5m (2 marks)
1. Wholesaler paid 120 × 500 = sh 600
  100
  Retailer paid 130 × 600 = sh 780
  100
  Customer paid 150 × 780 = sh 1170
  100 (3 marks)
2. Let the amount paid by wholesaler be x
  Retailer paid ¹³⁰/₁₀₀x = 1.3x
  Cutomer paid ¹⁵⁰/₁₀₀ × 1.3x = 1.95x
  ∴ 1.95x = 1560
  x = 1560
  1.95
  = Sh. 800 (3 marks)
3. Without the slae customer would have paid (4 marks)
  1000 × 120 × 130 × 150 = Sh.2340
  100 100 100
  Less 10% reduction = ⁹⁰/₁₀₀ × 2340
  ⇒ Selling price (SP) = Sh 2106
  Buying Price (BP) for retailer
  = 1000 × ¹²⁰/₁₀₀ × ¹³⁰/₁₀₀
  = Sh. 1560
  ∴ %profit = 2106 − 1560 × 100
  1560
  =35%
1. Area of front & back walls = 6.3 × 3.2 × 2
  =40.32m²
  Area of side walls = 4.5 × 3.2 × 2
  =28.2m²
  Area of floor = 6.3 × 4.5
  = 28.35m²
  Total area of floor and walls = 40.32 + 28.8 + 28.35
  = 97.47m²
  Area of door = 1.85 × 0.8 = 1.48m²
  Area of windows = 1.5 × 0.7 × 4 = 4.2m²
  Total area not cemented = 1.48 + 4.2
  = 5.68m²
  ∴ Area to be cemented = 97.47 − 5.68
  = 91.79 = 91.8m² (5 marks)
2. Cost of cementing materials = 91.8 × 500
  = sh. 45,900 (2 marks)
3. Cost of labour = 20% of sh 45900
  =²⁰/₁₀₀ × 45900
  = sh 9180
  Total cost of cementing = 45900 + 9180
  = sh. 55,080 (3 marks)
1. 1. Mombasa to Mtito Andei time
    = (2400 − 1930) + 2:50 = 4:30+2:50
    =7h 20 min
  2. Mtito Andei to Nairobi time
    =1050 − 0335 = 7h 15min
  3. Nairobi to Nakuru time
    =1900 − 1240 = 6h 20min
  4. Nakuru to Kisumu time
    =(2400 − 2015) + 9:00 = 3:45 + 9
    = 12h 45min (4 marks)
2. Stoppage time at Mtiti Andei
  = 0335 − 0250 = 45min
  Stoppage time at Nairobi
  =1240 − 1050 = 1h 50min
  Stoppage time at Nakuru
  =2015 − 1900 = 1h 15min
  Total stoppage time
  =45min + 1h 50min + 1h 15min
  =3h 50min
  Travellinig time from Mommbasa to Kisumu
  =7h 20min + 7h 15min + 6h 20min + 12h 45min = 33h 40min
  Time for whole journey
  = 33h 40min + 3h 40min
  =37h 30min (4 marks)
3. Average speed = Distance covered = 1200
  Time taken 37.5
  =32km/h (2 marks)
1. 1. Area of whole sheet = 80 × 50 cm²
    Area of sheet removed = 5×5×4cm²
    ∴ area of remaining part
    =(80 × 50) − (5×5×4)
    =4000 − 100
    =3900cm² (2 marks)
  2. Volume of metal cuboid = 3900 × 0.2
    = 780cm³
    mass of empty cuboid = mass of metal
    = volume × density
    = 780 × 2.5g
    = 780 × 2.5 kg
    1000
    =1.95kg (4 marks)
2. Dimensions of the cuboid are l = 80 − 10 = 70cm
  w = 50 − 10 = 40cm, h=5cm
  Capacity of cuboid = 70 × 40 × 5cm³Mass of water = volume × density
  = 70 × 40 × 4 × 1g
  = 70 × 40 × 4 ×1 kg
  1000
  =14kg (4 marks)
1. 1. x −2 −1 0 1 2 3 4 5
    
    y 13 10 7 4 1 −2 −5 −8
  2. x −4 −2 0 2 4 6 8 10
    
    y −16 −12 −8 −4 0 4 8 12
2. Scale used:
  Horizontal axis; 1cm rep. 2 units
  Vertical axis: 2cm rep 5 units
  (4 marks)
3. Both graphs are straight lines 1 marks)
4. x=3, y = −2 (1 marks)
AP=40m
AQ = 100m
AR = 130m
AD = 250m
PB = 80m
QE = 60m
RC = 180m
Area of ∆ APB = ½ × 40 × 80 = 1600m²
Area of ∆ AQE = ½ × 100 × 60 = 3000m²
Area of trapezium BPRC = ½(80 + 4=100)90 = 8100m²
Area of ∆ DQE = ½ × 150 ×60 = 4500m²
Area of ∆ DRC = ½ × 120 × 100 = 6000m²
By addition, area of ABCDE =23200m²
∴ area of field = 2.32ha