Mathematics Questions and Answers - Form 2 Term 1 Opener Exams 2022

Share via Whatsapp

Next Topic »
English Questions and Answers - Form 2 Term 1 Opener Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS TO STUDENTS

All answers and workings must be written on the question paper in the spaces provided below each question
Show all step in your calculation , giving your answers at each stage in the spaces provided below each question
Marks may be given for correct working even if the answer is wrong
Electronic calculators and mathematical tables may be used except where stated otherwise
Take π =22/7

Questions

SECTION 1(50MKS)

Evaluate without using a calculator. (3mks)
4 of 20+10÷-5×6
6×9-4÷2+12
0.24+-0.3×-0.81 (3mks)
0.08÷0.4
1. Find the H.C.F of 36 and 54 (1mk)
2. If three numbers 36,54 and another number have a G.C.D of 6 and L.C.M of 216, find the other number (2mks)
1. Simplify the expression (3mks)
  3x+4 + x+1 - 2x+8
  4 2 3
2. Solve for x in the equation below.
  2(x+4) =14 (2mks)
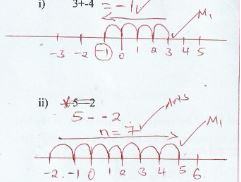
Use a number line to work out the following:
1. 3+-4 (1mk)
2. 5 - - 2 (1mk)
The length of an arc of a circle is 88cm. Find the radius of the circle if the arc subtends an angle 144° at the centre (Take =22/7) (3mks)
Four men can build a stone wall 32m long in 12 days . What length of wall can eight men, working at the same rate , build in eight days.Give your answer to 4 significant figures (3mks)
A shopkeeper made a loss of 20% by selling a trouser at Sh. 960 . What profit would he have made if he had sold it at sh.1500 (3mks)
A girl spent ²/₅ of her pocket money on bread and ¹/₆ of the remainder on stationery. If she had Ksh. 200 left at the end of the term, how much pocket money did she have at the beginning of the term. (3mks)
Small cubes of of edge 2cm are to be packed into a rectangular container measuring 6 cm by 5 m and 4 m.How many cubes are required ? (3 mks)
a: b =2: 3 and b: c=5:9 , find the ratio a:c (2mks)
. .
Express 0.407as a fraction. (3mks)
Three bells ring at intervals ring at intervals of 40 minutes,45 minutes and 60 minutes.If they ring simultaneously at 6.30 am,at what time will they ring next together? (3mks)
The area of 10 square plots is 160 ares .Find the length in metres of the side of each plot (3mks)
Find the perimeter of a circular protractor whose radius is 14 cm (3mks)
Convert the following decimals into percentage (3 mks)
1. 0.67
2. 1.25
3. 0.167

ANSWER ALL THE QUESTIONS IN THIS SECTION
SECTION II (50MKS)

1. A cylindrical can of diameter 20 cm and height 60cm is filled with water using a cylindrical jar of diameter 10 cm and height 8 cm. How many jarfuls will fill the can? (5 mks)
2. Find the the surface area of an isosceles triangular prism of length 25 cm ,height 4.5 cm and base 6 cm (5 mks)
1. Find the area of the sector of a circle of radius 3 cm if the angle subtended at the centre at the centre is 1400 .(Take pie=22/7) (4mks)
2. A minor arc of a circle subtends an angle of 1050 at the centre of the circle.If the radius of the circle is 8.4 cm,find the length of the major arc (3 mks)
3. Calculate the surface area of a rectangular tank measuring 5.4 cm long,3.6 cm width and 1.8 cm high. (3 mks)
1. All prime numbers less than ten are arranged in descending order to form a number
  1. Write down the number formed (2 mks)
  2. State the total value of the second digit in the number formed in a(i) above (2 mks)
2. The lengths of wires were 30 m,36 m and 84 m.Pieces of wire of equal length were cut from the three wires.Calculate the least number of pieces obtained. (6 mks)
1. When a certain number is divided by 30,45 or 54 there is always a remainder of 21.Find the number (4 mks)
2. A square toilet is covered by a number of whole rectangular tiles of sides 60 cm by 48 cm. Calculate the least possible area of the room in square metres (3 mks)
3. 1. Express 1050 in terms of its prime factors (1 mk)
  2. Determine the smallest positive number such that 1050P is a perfect square (2 mks)
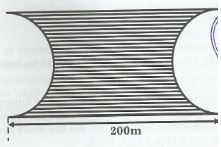
The following figure represents a piece of land . The two ends are semicircles of radius 70m each.
1. Calculate
  1. The perimeter of the land (2mks)
  2. The area of the land in hectares (3mks)
2. A private developer bought this piece of land at a price of Ksh 5,000,000 per hectare and later sold the all land at Kshs. 14,760,000. Determine
  1. The price at which he bought the whole piece of land (2mks)
  2. His percentage profit (3mks)

Marking Scheme

- Numerator:
  = 80 + 10
  =80-2(6)
  80-12
  =68
  Denominator:
  54 - 2 + 12
  52+12
  64
- 0.24 + 0.243= 0.483
  0.08 ÷ 0.4= 0.2
  0.483
  0.2
  = 2.415
1. 2 36 54
  
  3 18 27
  
  3 6 9
  
  2 3
  
  2 x 3 x 3= 18
2. Other number: gcd x lcm
  given number
  6 x 216 = 36
  36
  6 x 216 = 24
  54
1. 3(3x+4) + 6(x+1) - 4(2x+8)
  12
  9x+12 + 6X+6-8x-32
  12
  7x-14
  12
2. 2x+8=14
  2x=14-8
  2x=6
  x=3
Length of an arc = ^θ/₃₆₀2πr
88cm = 144/360 x 2 x 22/7 x r
88x10=88/7r
r=880 x 7
88
r=70cm
Men Length Days
4 32 12
8 ? 8
Ratio of men; 8:4 = 2:1
Ratio of days 8:12 = 2:3
Length of wall= ²/₁ x ²/₃ x 32 = ¹²⁸/₃ = 42.67
80% = 960
100%=?
100 x 960 = 1200
80
1500 - 1200 = 300
³⁰⁰/₁₂₀₀ x 100 = 25%
Bread = 2/5
5/5 - 2/5 = 3/5
Stationery = 1/6 of 3/5 = 1/10
2/5 + 1/10 = 1/2
1/2 → 200
2 x 200 = 400
1
1US dollar = 90.45
7500
7500 x 90.45 = 678, 375
1
678, 375 - 638, 676 = 39, 699
1 Sterling pound= 132.33
? = 39699
39699 = 300
132.33
a:b = a:b:c
5(2:3) = 10:15
b:c
3(5:9)= 15:27
a:c = 10:27
Let r = 0.4074
10r= 4.0740
100r = 40.7407
1000r= 407.4074
999r= 407
r= 407/999
r=¹¹/₂₇
2 40 45 60

2 20 45 30

2 10 45 15

3 5 45 15

3 5 15 5

5 5 5 5

1 1 1

2 x 2 x 2 x 3 x 3 x 5 = 360
360/60 = 6hrs
6:30 + 6= 12:30pm
1are= 100m²
16ares= ?
16 x 100= 1600m²
√1600 = 40m
1 side = 40m
½πD +D
d= 14 x 2= 28
²²/₇ x ¹/₂ x 28 + 28
11 x 4 + 28
44 + 28 = 72
1. 0.67
  ⁶⁷/₁₀₀x 100= 67%
2. ^1.25/₁₀₀ x 100 = 125%
3. ¹⁶⁷/₁₀₀₀ x 100 = 16.7%
1. V= πr²h
  1 ----- 22/7 x 10 x 10 x 60 = 132000/7
  2------ 22/7 x 10 x 10 x 8 = 17600/7
  132000 x 7
  7 17600
  =7.5
  jarfuls= 8
1. 140/360 x 22/7 x 3 x 3
  = 2/4 x 22= 11cm²
2. 360-105 = 255 - major arc
  length= circumference= 255/360 x 22/7 x 2(8.4)
  255/360 x 22/7 x 16.8
  255/360 x 22 x 2.4
  255/150 x 22 = 37.4cm
3. Sa= 2(5.4 x 3.6)+2(5.4 x 1.8)+2(3.6 x1.8)
  =2(19.44)+2(9.72)+2(6.48)
  =38.88+19.44+12.96
  =71.28
1. 1. 75321
  2. 20
2. 30, 36,84 -----GCD
  
  2 30 36 84
  
  3 15 18 42
  
  5 6 14
  
  2 x 3= 6m ---equal length
  30/6 = 5 pieces
  36/6 = 6 pieces
  84/6 = 14 pieces
  5 + 6 + 14 = 25 pieces
1. 30, 45, 54 -----LCM
  
  2 30 45 54
  
  3 5 45 27
  
  3 5 15 9
  
  3 5 5 3
  
  5 5 5 1
  
  1 1 1
  
  2 x 3 x 3 x 3 x 5 = 270
  
  270 + 21 = 291
2. 60,48 ----LCM
  
  2 60 48
  
  2 30 24
  
  2 15 12
  
  2 15 6
  
  3 15 3
  
  5 5 1
  
  1 1
  
  2 x 2 x 2 x 2 x 3 x 5 = 240
  240 cm = 2.4m
  2.4 x 2.4 = 5.76m²
3. 1. 1050 → 2 x 525
    2 x 3 x 175
    2 x 3 x 5 x 35
    2 x 3 x 5 x 5 x 7
  2. 1050 = 2 x 3 x 5 x 5 x 7
    1050P = 2 x 2 x 3 x 3 x 5 x 5 x 7 x 7
    P = 2 x 3 x 7= 42
    P= 42
1. 1. 1. Perimeter = 2 (1/2πD + 200)
      2( 1/2 x 22/7 x 140 + 200)
      2(220 + 200)
      = 2(420)
      = 840m
    2. area = (200 x 140) - 2(1/2 x 22/7 x 70 x 70)
      =28000 - 15400 =12600
      12600m²12600/10,000 = 1.26ha
2. 1. 1.26 x 5,000,000 = 6 300 000
  2. 6 300 000 = 100%
    14 760 000 =?
    14 760 000 x 100 = 234.2857
    6 300 000
    234.2857 - 100 = 134.2857%

Mathematics Questions and Answers - Form 2 Term 1 Opener Exams 2022

Questions

Marking Scheme

Download Mathematics Questions and Answers - Form 2 Term 1 Opener Exams 2022.

Why download?

Related items

What does our community say about us?

Join our community on:

2	30	45	54
3	5	45	27
3	5	15	9
3	5	5	3
5	5	5	1
	1	1	1
2 x 3 x 3 x 3 x 5 = 270