Mathematics Questions and Answers - Form 2 Mid-term Exams Term 1 2022

QUESTIONS

INSTRUCTIONS: Answer all questions in the spaces provided

1. Simplify 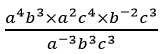  (3mks)
2. Using mathematical tables, find the value of (3mks)
   1. 456 × 397
          273
   2. 0.1468³+      1      (2mks)
                       27.38
3.                
   1. Determine the gradient and the y-intercept of the following equation (3mks)
      ¹/₃ x + ²/₅ y+¹/₆ = 0
   2. Find an equation perpendicular to the line 2y=3x+4 and passing through point (2, 6) (4mks)
4. The volume scale factor of two similar cylinders is 27. Find;
   1. The linear scale factor (2mks)
   2. The area scale factor (1mk)
5. By substitution method, solve the following simultaneous equations
   2x + 4y = 16
   3x - y = 2 (3mks)
6. A quadrilateral has vertices P(-3,7), Q(-5,3), R(-3,1), and S(-1,3).
   1. On the grid provided, draw the quadrilateral and name it (2mks)
      
   2. Find the equation of the line of symmetry of the quadrilateral formed in (a) above. (2mks)
   3. Draw the image of quadrilateral PQRS under a reflection in the line y=x and give the coordinates of the image. (3mks)
   4. Find the equation of the line of symmetry of the image (2mks)

MARKING SCHEME

INSTRUCTIONS: Answer all questions in the spaces provided

1. Simplify 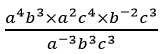  (3mks)
   (a × a × a × a)  × ( b × b × b) × (a × a) × (c × c × c  × c)  × (b^-1  × b^-1) × (c × c × c) 
                        (a^-1 × a^-1 × a^-1) × (b × b × b)  × (c × c × c)
   a³× a²× c⁴× b^-2
             a^-3
   
2. Using mathematical tables, find the value of (3mks)
   1. 456 × 397
          273
      

      No	Std form	Log
      456	4.56 × 102	2.6590
      397	3.97 × 102	+ 2.5988
      		- 5.2578
      273	2.73 × 102	2.4362
      		2.8216

      2.8216
      0.8216 × 10²
      Anilog of 0.8216
      = 6.63132 × 10²
      = 663.132
   2. 0.1468³+      1      (2mks)
                       27.38
      

      No	Std Form	Log
      0.14683	(1.468 × 10-1)3	3.1635 × 10-3
      1/27.38	1/2.738 × 101	1/10 × 0.3655

      = 0.03655
      + 0.003165
       0.039715
       = 0.039715
3.                
   1. Determine the gradient and the y-intercept of the following equation (3mks)
      ¹/₃ x + ²/₅ y+¹/₆ = 0
      5/2 × 2/5y = -1/6 ^{× 5/2} - 1/3x ^{× 5/2}
      y = (-1/6 × 5/8) - 1/3x × 5/2
      y = 5/48 - 5/6x
      Gradient = -5/6
   2. Find an equation perpendicular to the line 2y=3x+4 and passing through point (2, 6) (4mks)
      M₁M₂ = -1
      2y = 3x + 4
      2      2      2
      y = 3/2x + 2
      M₁ = 3/2
      2/3 × 3/2 × m₂ = -1 × 2/3
      m₂ = -2/3
      y - 6 = 2
      x - 2    3
      3y - 18 = -2x + 4
      3y = 2x + 22
      3      3      3
      y = -2/3x + 22/3
4. The volume scale factor of two similar cylinders is 27. Find;
   1. The linear scale factor (2mks)
      3√27 = 3
      L.S.F = 3
   2. The area scale factor (1mk)
      A.S.F = (L.S.F)²
      32 = 9
5. By substitution method, solve the following simultaneous equations
   2x + 4y = 16
   3x - y = 2 (3mks)
   2x(2x + 4(3x - 2)) = 16
   2x + 12x - 18 = 16
   14x = 24
   14     14
   x = 12/7
   y = 3x - 2
   y = (3 × 12/7) - 2
   y = 36/7 - 2/1
   y = 36 - 14
            7
   y = 22/7
6. A quadrilateral has vertices P(-3,7), Q(-5,3), R(-3,1), and S(-1,3).
   1. On the grid provided, draw the quadrilateral and name it (2mks)
      kite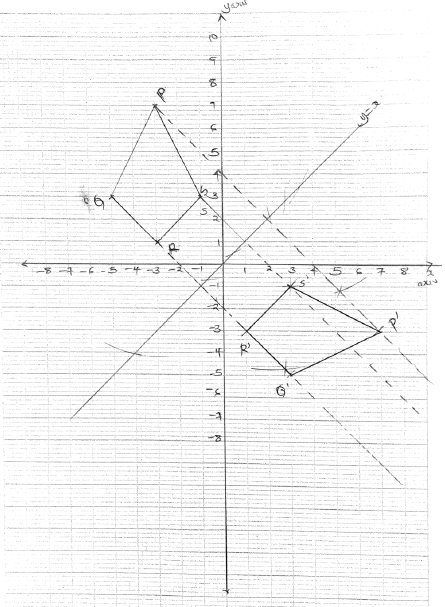
      
   2. Find the equation of the line of symmetry of the quadrilateral formed in (a) above. (2mks)
      P(-3,7) and R(-3,1)
      therefore gradient = -3
   3. Draw the image of quadrilateral PQRS under a reflection in the line y=x and give the coordinates of the image. (3mks)
      P₁ = (7, -3)
      Q₁ = (3, -5)
      R₁ = (1, -3)
      S₁ = (3, -1)
   4. Find the equation of the line of symmetry of the image (2mks)
      P(7, -3)
      R(1,-3)
      Gradient y = -3