QUESTIONS
SECTION I (40 Marks) - Answer all questions in this section.
-
- Use the table of cubes to evaluate 23.53 (2 mark)
- Find the cube root of 3.375 using prime factor method (2marks)
- Evaluate using the table of reciprocals: 2.5 + 2 (marks)
0.0842 64.5 - Simplify the expression ∛27x3y9 (2 marks)
x6y3 - Use logarithm tables to evaluate: 2√124.4 × 35.8(3 marks)
745 - Solve for x given that 2x × 8x ÷ 4 = 64 (3 marks)
- A bank in Kenya buys and sells foreign currencies as follows.
Currency Buying(Ksh) Selling(Kshs)
1Sterling 134.20 134.65
1US dollar 71.40 71.84
A tourist arrived in Kenya with 4500 US dollars. He converted all the dollars to Kenya shillings at the bank. While in Kenya he spent Kshs 215,000 and then converted the remaining amount to sterling pounds in the same bank. Calculate the amount he received in sterling pound. (3marks) - The length of an arc of a circle is 8.8cm. If the arc subtends an angle 144° at the centre, calculate;
- the radius of the circle (Take π=22/7) (2 marks)
- the area enclosed by the arc and the radii (2 marks)
- Determine the number of sides of a regular polygon whose sum of interior angles is 1440º. (2marks)
- A shopkeeper made a loss of 20% by selling a trouser at Sh. 960. What profit would he have made if he had sold it at sh.1500 (3marks)
- A student spent 2⁄7 of his pocket money on stationeries, a third on food-stuffs and 5⁄8 of the remainder on transport. If he had Ksh. 150 left, how much pocket money did he have at the beginning? (3marks)
- Two bells ring at intervals of 35 and 42 minutes respectively. The bells ring together at 8:48 a.m. Determine the time when the bells will ring together again. (3 marks)
- A two-digit number is 18 more than the number formed by reversing the digits. If the sum of the digits is 10. Find the number. (3 marks)
- Evaluate; (3 marks)
14÷1/3 of 5¼ - 3¾ × 11/3
SECTION II (30Marks)
Answer any THREE questions
- The figure below represents a piece of land consisting of a trapezoidal region and a semi-circular end of radius 87.5m
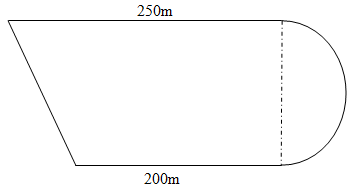
- Calculate
- The perimeter of the land (3marks)
- The area of the land in hectares (3marks)
- A private developer bought this piece of land at a price of Ksh 400,000 per hectare and later sold the all land at 2.25 million shillings. Determine;
- The price at which he bought the whole piece of land (2marks)
- His percentage profit (2marks)
- Calculate
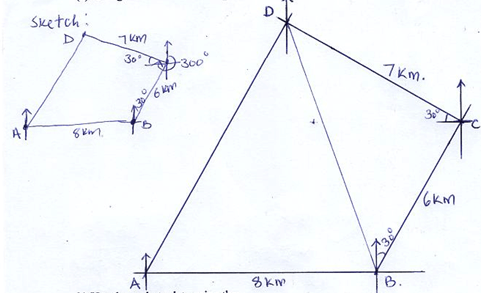
- The corner points A, B, C and D of a ranch are such that B is 8 km directly East of A and C is 6 km from B on a bearing of 30º. D is 7 km from C on a bearing of 300º.
- Using a scale of 1 cm to represent 1 km, draw a diagram to show the position of A, B, C and D. (4 marks)
- Use the scale to determine the;
- compass bearing of A from D. (1 mark)
- distance BD in kilometers. (2 marks)
- bearing of D from B (1 mark)
- perimeter of the ranch in kilometers. (2 marks)
-
- A straight line L1, whose equation is 3y - 2x = -2 meets the x-axis at R. Determine the coordinates of R. (2 marks)
- A second line L2 is perpendicular to L1 at R. Find the equation of L2 in the form y = mx +c, where m and c are constants. (3 marks)
- A third line L3 passes through (-4, 1) and is parallel to L2. Find:
- the equation of L3 in the form y = mx +c, where m and c are constants. (2 marks)
- The coordinates of a point S, at which L1 and L3 intersects (3 marks)
- A cylindrical tank of diameter 3.6m and height 2.5m internally is two-thirds full of juice.
- Calculate the volume of the juice in litres. (3 marks)
- The juice is packed in small packets measuring 8cm by 5cm by 12cm. A packet retails at Kes. 40. Calculate;
- the capacity of each packet in cm3 (2 marks)
- the number of full packets obtained (3 marks)
- the amount of money realized from the sale of the juice (2 marks)
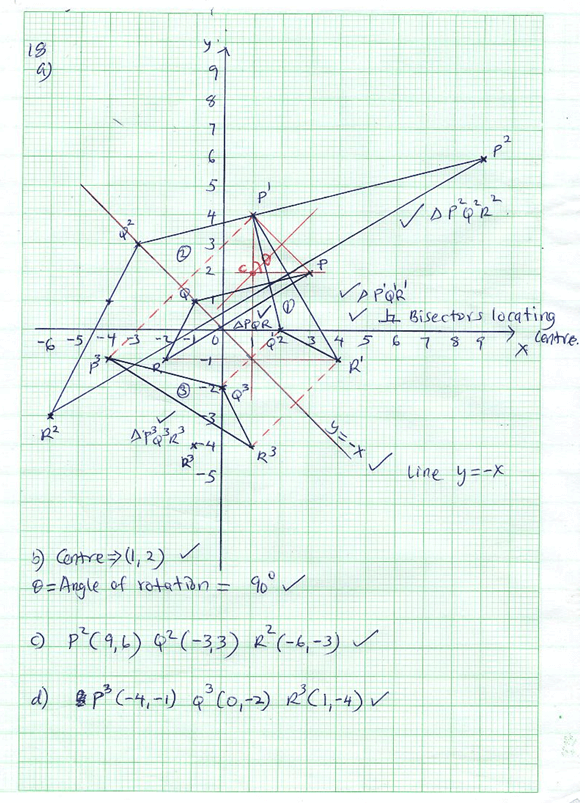
- Triangle PQR has vertices P(3,2), Q(-1,1) and R(-2,-1).
- Draw PQR on the grid provided. (1mark)
- Under a rotation the vertices of P1Q1R1 are P1(1,4), Q1(2,0) and R1(4,-1). Find the centre and angle of rotation using points P and Q. (4marks)
- Triangle PQR is enlarged with scale factor 3 centre O (0,0) to give triangle P2Q2R2. Draw triangle P2Q2R2 and state its co-ordinates. (2marks)
- Triangle P1Q1R1 undergoes reflection in line y = -x to give triangle P3Q3R3. Draw P3Q3R3 and state its coordinates. (3mks)


MARKING SCHEME
-
- 23.53 = (2.35 x 101)3
= 12.978 x 103
= 12,978 - 3√3.375 = 3√3375 = 3√3375
103 10
3375 = 3 x 3 x 3 x 5 x 5 x 5
3√3375 = 3 x 5 = 15
3√3.375 = 15/10
= 1.5
- 23.53 = (2.35 x 101)3
- 2.5(8.42-1 x 102) + 2(6.45-1 x 10-1)
8.42-1 = 0.1188
6.45-1 = 0.1550
= 2.5(0.1188 x 102) + 2(0.1550 x 10-1)
= 29.7 + 0.0310
= 29.731 - [33.x3.y9]
x6.y3
= 3.x.y3
x2.y
= 3y2 or 3xy
x
Anti log 10.3883 x 10ºNo Log 124.4
x 35.82.0948
+ 1.5339÷ 745 3.6487
- 2.8722√x 0.7765 x ½
0.3883
= 2.445- 2x x 23x ÷ 22 = 26
2(x + 3x - 2) = 26
2(4x - 2) = 26
4x - 2 = 6
4x/x = 8/4
x = 2 - $ to Ksh
=4500 x 71.40
= Ksh 321,300
Less expenditure:
321,300 - 215,000
=Ksh 106,300
Ksh to £
=106,300
134.65
= £789.45 -
- L = 8.8cm
θ = 144º
r = ?
8.8 = 144/360 x 2 x 22/7 x r
r = 8.8 x 360 x 7
144 x 2 x 22
r = 22,176
6,336
r = 3.5cm - A = θ/360 x πr2
= 144 x 22/7 x 3.5 x 3.5
A = 15.4cm2
- L = 8.8cm
- sum = 180(n-2)
1440 = 180(n-2)
180 180
8 = n-2
n = 8+2
n = 10sides - 80% of B.P = S.P
80/100 x B.P = 960
B.P = 960 x 100/80
= Ksh1,200
If S.P = Ksh1500
Profit = 1500 - 1200 = 300
= Ksh 300 - Let pocket money = x
Stat + food = 2/7x + 1/3x
= 13/21x
Trans = 5/8 (x - 13/21x)
= 5/8 x 8/21x
= 5/21x
Total = 13/21x + 5/21x = 18/21x
Rem = x - 18/21x = 3/21x
But 3/21x = 150
x = 150 x 21/3
x = Ksh1050 - LCM =
LCM = 2 x 3 x 5 x 72 35 42 3 35 21 5 35 7 7 7 7 1 1
= 210min
210/60 = 3hr 30min
Time = 8:48 am + 3:30 = 11:78
= 12:18P.M - Let No be XY
(10x + y) - (10y + x) = 18
10x + y - 10y - x = 18
9x - 9y = 18 ...(i)
Also, x + y = 10...(ii)
Solving simultaneously;
1/9(9x - 9y = 18)
x + y = 10
+
x - y = 2
2x + 0 = 12
6 + y = 10
x = 6
y = 4
XY is 64 - 14 ÷ 7/4 - 15/4 x 4/3
= 14 x 4/7 = 8
15/4 x 4/3 = 5
8 - 5 = 3
SECTION II
-
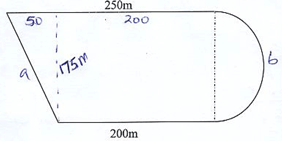
-
- a2 = 1752 + 502
a = 33125
a = 182.002m
b = ½ x 22/7 87.5m
b = 137.5m
Perimeter : 182.002 + 250 + 137.5 + 200
P = 769.502m - A1 = ½ x (250 + 200) x 175
½ x 450 x 175
= 39,375m2
A2 = ½ x 22/7 x 87.52
= 12.031.25m2
Total A = 39,375
+ 12,031.25m2
Total A = 51,406.25
10,000
= 5.140625ha
- a2 = 1752 + 502
-
- B.P = 5.140625 x 400,000
Ksh 2,056,250 - % profit = (2,250,000 - 2,056,250) x 100
2,056,250
= 9.422%
- B.P = 5.140625 x 400,000
-
-
-
-
- 530ºW
- B.D = 9.2cm x 1km/cm
= 9.2km ± 0.1km - 340º or N20ºW
- AD = 10Km ± 0.1km
Perimeter = 8 + 6 + 7 + 10
P = 31km ± 0.1km
-
-
- At x-axis y = 0
3y - 2x = -2
0 - 2x/-2 = -2/-2
x = 1
R is (1,0) - M1 = 2/3, m1m2 = -1
2/3.m2 = -1
m2 = -3/2
using (1,0) (x,y)
y-0 = -3/2
x-1
y = -3/2 (x - 1)
y = -3/2x + -3/2 -
- m2 = m3 = -3/2
Using(-4, 1)(x,y)
y -1 = -3/2
x + 4
y - 1 = -3/2 (x + 4)
y - 1= -3/2x - 6
y = -3/2x -5 - 2/3x -2/3 = y
-3/2x - 5 = y
At intersection
2/3x - 2/3 = -3/2x - 5
2/3x + 3/2x = -5 + 2/3
6/13 . 13/6x = -13/3.6/13
x = -2
y = 2/3(-2)-2/3
y = -4/3 - 2/3
y = -2
5(-2,-2)
- m2 = m3 = -3/2
- At x-axis y = 0
-
- V = 2/3 x 22/7 x 1.82 x 2.5
= 16.97143m3
1m3 = 1000l
V = 16.97143 x 1000
= 16,971.43l -
- V= 8 x 5 x 12cm3
=480cm3 - 1pct = 480cm3 = 480ml
1000
= 0.48l
No of pcts = 16,971.43
0.48
= 35,357.145
Full pets = 35,357 - Sales = 35,357 x 40
= Ksh 1,414,280
- V= 8 x 5 x 12cm3
- V = 2/3 x 22/7 x 1.82 x 2.5
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 2 Term 2 Opener Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

