QUESTIONS
SECTION A (50MKS)
Instructions.
Answer all questions in this section in the spaces provided.
- Use logarithms to evaluate. (4mks)
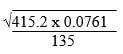
- Three similar bars of length 200 cm , 300cm and 360 cm are cut into equal pieces. Find the largest possible area of square which can be made from any of the three pieces.(3mks)
- A triangle has vertices A(2,5), B(1, -2) and C(-5,1). Determine:
- The equation of the line BC. (3mks)
- The equation of the perpendicular line from A to BC. (3mks)
- The ratio of the radii of two spheres is 2:3. Calculate the volume of the first sphere if the volume of the second is 20cm3. (3mks)
- Without using a mathematical table or calculator solve the following. (3mks)
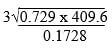
- Three boys shared some money, the youngest boy got ½ of it and the next got 1/9, and the eldest got the remainder. What fraction of money did the eldest receive? If the eldest got sh 330, what was the original sum of money? (4mks)
- Ten men working 6 hours a day take 12 days to complete a job. How long will it take 8 men working 12 hours a day to complete the same job? (3mks)
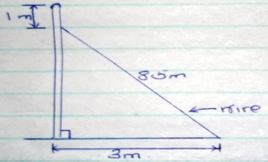
- An electric pole is supported to stand vertically by a tight wire as shown below. Find the height of the pole and leave to 2 decimal places. (3mks)
- From a window 25m above a street, the angle of elevation of the top of a wall on the opposite side is 15º. If the angle of depression of the base of the wall from the window is 35º find:
- The width of the street. (2mks)
- The height of the wall on the opposite side. (2mks)
- Simplify: (2mks)
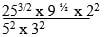
- Solve the in equality: (3mks)
2x – 1 ≤ 3x + 4 < 7 – x - Solve the following: (3mks)
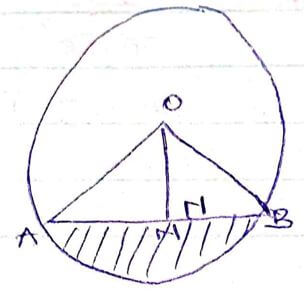
x2 + 3x – 54 = 0 - The figure below shows a circle with centre O and radius 5cm. if ON= 3cm, AB = 8cm and <AOB= 106.3º. Find the area of shaded region. (3mks)
- Expand and simplify: (2mks)
4(q + 6 ) + 7 (q – 3) -
- The length of a rectangle is three times its breadth. If its perimeter is 24cm what is the length of the rectangle. (2mks)
- Area of rectangle. (2mk)
SECTION B
Answer any two questions.
- A rectangular tank whose internal dimensions are 1.7m by 1.4m by 2.2m is filled with milk.
- Calculate the volume of milk in the tank in cubic metres. (2mks)
-
- The milk is to be packed in small packets. Each packet is in the shape of a right pyramid on an equilateral triangular base of side 16cm. The height of each packet is 13.6cm. Calculate the volume of milk contained in each packet. (3mks)
- If each packet was to be sold at sh 25 per packet, what is the sale realized from the sale of all exact packets of milk. (5mks)
- A triangle ABC with vertices A(-2,2), B (1, 4) and C(-1, 4) is mapped on to triangle A’B’C’ by a reflection in the line y=x+1.
- On the grid provided draw:

- Triangle ABC (1mk)
- The line y=x+1 (2mks)
- Triangle A’B’C’ (3mks)
- Triangle A’’B’’C’’ is the image of triangle A’B’C’ under a negative quater turn, with the centre of rotation as origin (0, 0). On the same grid draw triangle A”B”C” (4mks)
- On the grid provided draw:
- The following measurements were obtained while measuring a coffee field. The measurements were entered in a field book as follows:
Y 360 80 to Q 280 To R 80 200 To S 160 80 200 to P X - Taking the baseline XY = 400 m. draw the map of the coffee field using a scale of 1cm represents 40m.
- Calculate the area of the coffee field. (5mks)
- The figure below represents a right pyramid. On a square base of side 3cm. the slant edge of the pyramid is 4cm.
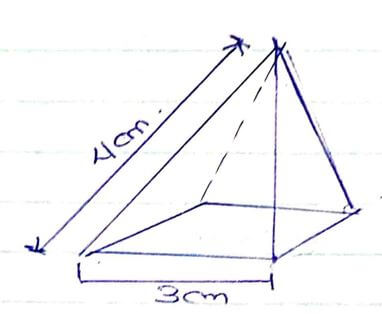
- Draw the net of the pyramid. (2mks)
- Calculate the surface area of the pyramid. (4mks)
- Calculate the volume of the pyramid to 2 decimal places. (4mks)
MARKING SCHEME
SECTION A (50MKS)
Instructions.
Answer all questions in this section in the spaces provided.
- Use logarithms to evaluate. (4mks)
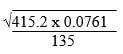
1 + 0.6847No Log 415.2 2.6182 0.0761 2.8814 1.4996 2.1303 135 3.3693
2= 4 + 1.3693
2 2
0.48378 <-- antilog
1.6847
Ans = 0.48378 - Three similar bars of length 200 cm , 300cm and 360 cm are cut into equal pieces. Find the largest possible area of square which can be made from any of the three pieces.(3mks)
GCD = 10 x 20 = 2010 200 300 360 2 20 30 36 10 15 18
area = 20 x 20 = 400 cm2 - A triangle has vertices A(2,5), B(1, -2) and C(-5,1). Determine:
- The equation of the line BC. (3mks)
y1 - y2 = 1 + 2 = -3 = -1
x1 - x2 -5 - 1 6 2
y + 2 = 1
x - 1 -2
-2 (y + 2) = 1(x - 1)
-2y - 4 = x - 1
-2y = x +3
-2y = x + 3 or y = -x/2 - 3/2 - The equation of the perpendicular line from A to BC. (3mks)
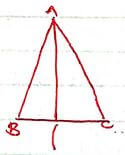
m1m2 = -1
-1/2 m2 = -1 m2 = 2
x1 + x2 y1 + y2
2 2
1 - 5 = -4 -2 + 1 = -1
2 2 2 2
(-2, -1/2)
y + 1/2 = 2
x + 2
y + 1/2 = 2(x + 2)
y = 2x + (4 - 1/2)
y = 2x + 31/2
y = 2x + 7/2 or 2y = 4x + 7
- The equation of the line BC. (3mks)
- The ratio of the radii of two spheres is 2:3. Calculate the volume of the first sphere if the volume of the second is 20cm3. (3mks)
LSF: 2:3
vsf:(lsf)3
vsf = (2:3)3 = 8:27
27 - 20cm3
20 x 8 = 5.926 cm3
27 - Without using a mathematical table or calculator solve the following. (3mks)
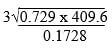
729 x 4096
1728
3 = √1728
= 12 - Three boys shared some money, the youngest boy got ½ of it and the next got 1/9, and the eldest got the remainder. What fraction of money did the eldest receive? If the eldest got sh 330, what was the original sum of money? (4mks)
x
youngest - 1/12x
middle - 1/9x
1/12x + 1/9x = 7/36
36/36 - 7/36 = 29/36 oldest
29/36 = 330
original = 330 x 36
29
= 409.65 - Ten men working 6 hours a day take 12 days to complete a job. How long will it take 8 men working 12 hours a day to complete the same job? (3mks)
No of men decreases 8:10
no of days increase 10:8
no of hours increase 12:6
no of days taken = 12 x 10/8 x 6/12
= 71/2 days - An electric pole is supported to stand vertically by a tight wire as shown below. Find the height of the pole and leave to 2 decimal places. (3mks)
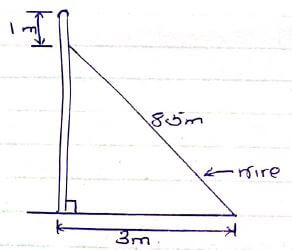
a2 + b2 = c2
852 - 32 = b2
b2 = 63.25
b = 7.95 + 1 = 8.59 m - From a window 25m above a street, the angle of elevation of the top of a wall on the opposite side is 15º. If the angle of depression of the base of the wall from the window is 35º find:
- The width of the street. (2mks)
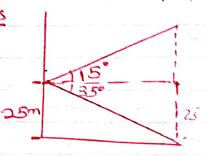
cos 35 = x/25
x = 25 cos 35
= 20.48m - The height of the wall on the opposite side. (2mks)
Tan 5 = x/20.48
x = 20.48 Tan 15
= 5.49 + 25
= 30.49m
- The width of the street. (2mks)
- Simplify: (2mks)
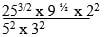
52 x 3 x 4 = 4
52 x 32 3 - Solve the in equality: (3mks)
2x – 1 ≤ 3x + 4 < 7 – x
2x - 1 = 3x + 4
2x - 3x = 4 + 1
-x = 5
4 -1
3x + 4 < 7 - x
3x + x = 7 - 4
4x = 3
4 3
x < 3 -5 ≤ x < 3/4 - Solve the following: (3mks)
x2 + 3x – 54 = 0
x(x - 6) + 9(x - 6) = 0
(x - 6)(x + 9) = 0
x = -9 or x = 6 - The figure below shows a circle with centre O and radius 5cm. if ON= 3cm, AB = 8cm and <AOB= 106.3º. Find the area of shaded region. (3mks)

area = area of sector - area of triangle
106.3 x 3.142 x 52
360
= 1/2 x 8 x 3
= 23.19 - 12
= 11.19 cm2 - Expand and simplify: (2mks)
4(q + 6 ) + 7 (q – 3)
4q + 24 + 7q - 21
11q + 3 -
- The length of a rectangle is three times its breadth. If its perimeter is 24cm what is the length of the rectangle. (2mks)

2(3x + x) = 24
8x = 24
x = 3
3x = 3 x 3 = 9 cm - Area of rectangle. (2mk)
l x w = A
9 x 3 = 27
= 27cm2
- The length of a rectangle is three times its breadth. If its perimeter is 24cm what is the length of the rectangle. (2mks)
SECTION B
Answer any two questions.
- A rectangular tank whose internal dimensions are 1.7m by 1.4m by 2.2m is filled with milk.
- Calculate the volume of milk in the tank in cubic metres. (2mks)
v = l x w x h
1.7 x 1.4 x 2.2
= 5.236m3 -
- The milk is to be packed in small packets. Each packet is in the shape of a right pyramid on an equilateral triangular base of side 16cm. The height of each packet is 13.6cm. Calculate the volume of milk contained in each packet. (3mks)

v = 1/3 bah
16 x 16 = 256 cm2 x 13.6 x 1/3
= 1160.5cm3 - If each packet was to be sold at sh 25 per packet, what is the sale realized from the sale of all exact packets of milk. (5mks)
1000000cm3 - 1m3
x 5.236m3
5236000
1160.5
= 4511.848
= 4511 packets
4511 x 25
= sh 112775
- The milk is to be packed in small packets. Each packet is in the shape of a right pyramid on an equilateral triangular base of side 16cm. The height of each packet is 13.6cm. Calculate the volume of milk contained in each packet. (3mks)
- Calculate the volume of milk in the tank in cubic metres. (2mks)
- A triangle ABC with vertices A(-2,2), B (1, 4) and C(-1, 4) is mapped on to triangle A’B’C’ by a reflection in the line y=x+1.
- On the grid provided draw:

- Triangle ABC (1mk)
- The line y=x+1 (2mks)
- Triangle A’B’C’ (3mks)
- Triangle A’’B’’C’’ is the image of triangle A’B’C’ under a negative quater turn, with the centre of rotation as origin (0, 0). On the same grid draw triangle A”B”C” (4mks)
- On the grid provided draw:
- The following measurements were obtained while measuring a coffee field. The measurements were entered in a field book as follows:
Y 360 80 to Q 280 To R 80 200 To S 160 80 200 to P X - Taking the baseline XY = 400 m. draw the map of the coffee field using a scale of 1cm represents 40m.
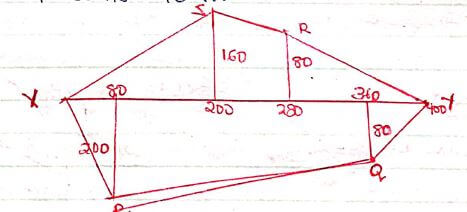
- Calculate the area of the coffee field. (5mks)
XP = 1/2 x 80 x 100 = 4000
PQ = 1/2 x (80 + 200)280 = 39200
PY = 1/2 x 40 x 80 = 1600
YR = 1/2 x 80 x 120 = 4800
RS = 1/2 x 80x (80 + 160) = 9600
SX = 1/2 x 200 x 160 = 16000
75200
10000
= 7.52 ha
- Taking the baseline XY = 400 m. draw the map of the coffee field using a scale of 1cm represents 40m.
- The figure below represents a right pyramid. On a square base of side 3cm. the slant edge of the pyramid is 4cm.

- Draw the net of the pyramid. (2mks)
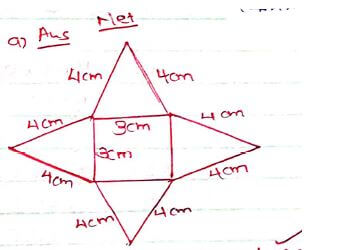
- Calculate the surface area of the pyramid. (4mks)
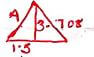
1/2 x 3 x 3.708 = 5.562
5.562 x 4 = 22.25
3 x = 9 9 +
31.25 cm2 - Calculate the volume of the pyramid to 2 decimal places. (4mks)
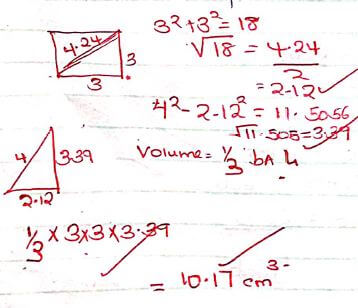
- Draw the net of the pyramid. (2mks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 2 End Term 2 Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

