INSTRUCTIONS TO CANDIDATES
- Write your name and index number in the spaces provided at the top of this page.
- This paper consists of two sections: Section l and Section II
- Answer all questions in section l and any five questions from Section II.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non- programmable silent electronic calculators and KNEC Mathematical tables may be used.

QUESTIONS
SECTION I(30 MARKS)
Answer ALL Questions from this section in the spaces provided
- Use logarithm tables ONLY, evaluate to 4 significant figures
 (4mks)
(4mks) - The sum of three consecutive odd integers is 219. Determine the first three such integers (3 mks)
- A Kenyan company received US Dollars 100,000.The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows:
Buying Selling
(in Kenya shillings) (in Kenya shillings)
1 US Dollar 77.24 77.44
1 Sterling Pound 121.93 122.27- Calculate the amount of money, in Kenya shillings, the company received. (2 mks)
- The company exchanged the Kenya shillings calculated in (a) above, into sterling pounds to buy a car from Britain. Calculate the cost of the car to the nearest sterling pound. (2 mks)
- A solid cone of height 12cm and radius 9 cm is recast into a solid sphere. Calculate the surface area of the sphere. ( 4 marks)
- The G.C.D of two numbers is 12 and their L.C.M is 240. If one of the numbers is 60, find the other number. (2mks)
- Solve for x in the equation: 6x2-13x+6=0 (3mks)
- Simplify without using tables 4 cos 450 sin 600 (2mks)
- Use mathematical tables only to evaluate 11.45 sin 38.3 (3mks)
- If the area of a regular nonagon is 185.1cm2. What is the length of each side? (3mks)
SECTION II (30 MARKS)
Answer ANY THREE Questions from this section in the spaces provided - A helicopter flies from Kaptiony due south for 300km. It then flies on a bearing of 2550 for 350km. From there it flies on a bearing for 0400 for 400km.
- Draw an accurate diagram showing the journey of the helicopter using a scale of 1:5000000. (5mks)
- From your diagram, find the distance and bearing of Kaptiony from the final position of the .helicopter. (2mks)
- Given that the helicopter flies at a steady speed of 200kmh-1, find how long the whole journey took. (3mks)
- The figure below shows two intersecting circles with centres P and Q and radius 5cm for the small one and 6cm for the big one. AB is a common chord of length 8cm. Calculate;
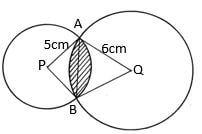
- the length of PQ (1 mark)
- the size of;
- angle APB (2marks)
- angle AQB (2 marks)
- the area of the shaded region(5 marks)
- Below are the measurements of a wheat field using a baseline XY recorded in metres.
Y
240
TO R 60
190
180
75 TO Q
150
50 TO P
TO S 100
120
100
100 TO N
TO T 30
50
20
20 TO M
X
- Using a scale of 1cm represents 20m. Sketch the map of the wheat field. (4mks)
- Find the area of the field in hectares. (4mks)
- If the cost of one hectare is sh65, 000 find the cost of the wheat field. (2mks)
- The figure below shows a glass in form of a frustum of a cone whose top and bottom diameter of 7cm and 3.5cm respectively. Its depth is 10cm. Taking π=22/7,
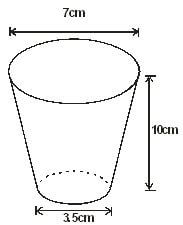
Calculate;- Its total surface area. (5 marks)
- Its capacity. (5 marks)

MARKING SCHEME
SECTION I(30 MARKS)
Answer ALL Questions from this section in the spaces provided
- Use logarithm tables ONLY, evaluate to 4 significant figures
 (4mks)
(4mks)
- The sum of three consecutive odd integers is 219. Determine the first three such integers (3 mks)
- let the numbers be a, b and c respectively such that:
a
b =a + 2
c = a + 2 + 2 = a + 4
a + (a+2) + (a+4) = 219
a + a + 2 + a + 4 = 219
3a + 6 = 219
3a = 213
a = 71
b = 73
c = 75
- let the numbers be a, b and c respectively such that:
- A Kenyan company received US Dollars 100,000.The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows:
Buying Selling
(in Kenya shillings) (in Kenya shillings)
1 US Dollar 77.24 77.44
1 Sterling Pound 121.93 122.27- Calculate the amount of money, in Kenya shillings, the company received. (2 mks)
- 7, 724, 000 (student should show working)
- 7, 724, 000 (student should show working)
- The company exchanged the Kenya shillings calculated in (a) above, into sterling pounds to buy a car from Britain. Calculate the cost of the car to the nearest sterling pound. (2 mks)
- 63, 171.669
to the nearest pound:
£ 63, 172
(student should show working.
NOte: € - is for Euro)
- 63, 171.669
- Calculate the amount of money, in Kenya shillings, the company received. (2 mks)
- A solid cone of height 12cm and radius 9 cm is recast into a solid sphere. Calculate the surface area of the sphere. ( 4 marks)
- S.A of cone = S.A of the sphere
S.A of cone = 2πr2 + πdh
= (2 x 22/7 x 9 x 9) + (22/7 x 18 x 12)
=3564/7 + 4572/7
=8136/7 = 1,162.2857cm2
- S.A of cone = S.A of the sphere
- The G.C.D of two numbers is 12 and their L.C.M is 240. If one of the numbers is 60, find the other number. (2mks)
- G.C.D = 12
let number be x
2 60 x 2 30 x/2 3 15 x/4 5 5 x/12 x/12 1
2 x 2 x 3 = 12 (The GCD),
hence x is not divisible by 5.x/12 1 1 2 x 2 x 3 x 5 x x/12 = 240
12 x 5 x x/12 = 240
5x = 240
x= 240/5
x= 48
- G.C.D = 12
- Solve for x in the equation: 6x2 -13x + 6 = 0 (3mks)
- 6x2 - 4x - 9x + 6 = 0
2x(3x - 2) -3(3x-2)= 0
(2x - 3)(3x -2)= 0
2x - 3= 0 hence 2x = 3, hence x = 2/3
3x - 2= 0 hence 3x = 2, hence x = 3/2
- 6x2 - 4x - 9x + 6 = 0
- Simplify without using tables 4 cos 450 sin 600 (2mks)
- 4 Cos (360 + 90) Sin (360 + 240)
- 4 Cos 90 Sin (240 - 180 - 3rd quadrant hence value is negative
- 4 Cos 90 - (Sin 60)
4 (0)- (0.86603)
= 0
- Use mathematical tables only to evaluate 11.45 sin 38.3 (3mks)
- 11.45 x 0.62251
7.1277395
- 11.45 x 0.62251
- If the area of a regular nonagon is 185.1cm2. What is the length of each side? (3mks)
- interior angle = 140
It forms iscosceles traing;les with angele of 70, 70 and 40.
S is the length of the equal sides ( lines from the edges of the nanogon to the center) ,
hence total area:
area = 9 x 1/2 x s2 x Sinθ
9 x 1/2 x s2 x sin 40 = 185.1
s2 = 185.1 x 2
9 x sin 40
370.1
9 x 0.64279
= 370.1/ 5.78511
s2= 63.9745 approx = 64
s2 = 64
s = 8cm
Each of the 9 triangles can be split in th middle by a perpendicular line, to give a triangle with angles of 20, 70 and 90.
to find length of the lower side:
x = 8 Sin 20
x =2.73616
2x = 5.47232 cm
Length of side = 5.47232 cm
SECTION II (30 MARKS)
Answer ANY THREE Questions from this section in the spaces provided
- interior angle = 140
- A helicopter flies from Kaptiony due south for 300km. It then flies on a bearing of 2550 for 350km. From there it flies on a bearing for 0400 for 400km.
- Draw an accurate diagram showing the journey of the helicopter using a scale of 1:5000000. (5mks)
- From your diagram, find the distance and bearing of Kaptiony from the final position of the .helicopter. (2mks)
- Given that the helicopter flies at a steady speed of 200kmh-1, find how long the whole journey took. (3mks)
- The figure below shows two intersecting circles with centres P and Q and radius 5cm for the small one and 6cm for the big one. AB is a common chord of length 8cm. Calculate;

- the length of PQ (1 mark)
7.472cm - the size of;
- angle APB (2marks)
- Sin θ = 4/5
Sin -1 0.8 = θ = 53.13 x 2
= 106.26 ± 1
- Sin θ = 4/5
- angle AQB (2 marks)
- Sin θ = 4/6
Sin -1 2/3 = θ = 41.8
41.8 x 2 = 83.6 ± 1
- Sin θ = 4/6
- angle APB (2marks)
- the area of the shaded region(5 marks)
- (83.6/360 x 22/7 x 6 x 6) - (2 x 1/2 x 4.472 x 4) = 26.27428 - 17.888 = 8.38628
- (106.26/360 x 22/7 x 5 x 5) - (2 x 1/2 x 3 x 4)
23.1916666667 - 12 = 11.1916666667
8.38628 + 11.1916666667 =
19.5779466667
(allow for erros of margin/ rounding off etc)
- the length of PQ (1 mark)
- Below are the measurements of a wheat field using a baseline XY recorded in metres.
Y
240
TO R 60
190
180
75 TO Q
150
50 TO P
TO S 100
120
100
100 TO N
TO T 30
50
20
20 TO M
X
- Using a scale of 1cm represents 20m. Sketch the map of the wheat field. (4mks)
- Find the area of the field in hectares. (4mks)
- If the cost of one hectare is sh65, 000 find the cost of the wheat field. (2mks)
- The figure below shows a glass in form of a frustum of a cone whose top and bottom diameter of 7cm and 3.5cm respectively. Its depth is 10cm. Taking π=22/7,

Calculate;- Its total surface area. (5 marks)
glass has open upper side, therefore:
TSA = area of bottom circle + area of middle part
bottom circle = 22/7 x 1.75 x 1.75= 9.625 cm2
middle part lengths:
22/7 x 3.5 = 11
22/7 x 7 = 22
Area = (2 x 1/2 x 5.5 x 10) + (11 x 10)
= 55 + 110 = 165
165 + 9.625 = 174.625cm2 - Its capacity. (5 marks)
Vol = 1/3 x 22/7 x 10 ( r12 + r22 + (r1 x r2))
Vol = 1/3 x 22/7 x 10 ( 3.52 + 72 + (3.5 x 7))
Vol = 1/3 x 22/7 x 10 ( 12.25 + 49 + 24.5)
Vol = 1/3 x 22/7 x 10 ( 85.75)
Vol = 1/3 x 22/7 x 857.5
898.333333333 cm3
- Its total surface area. (5 marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 2 Mid Term 2 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

