Mathematics Questions and Answers - Form 2 Mid Term 1 Exams 2023

• This paper consists of two sections: Section I and Section II.
• Answer all questions in section I and Section II.
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong.
• KNEC Mathematical tables may be used.

SECTION I (50 Marks)    
Answer all the questions in the spaces provided

1. One tablespoon of Sodium chloride is made by mixing 12 mg of sodium and 15g of chlorine. Determine the mass of the mixture in kilograms and express in standard form.      (3 marks)
2. The odd numbers less than 10 are multiplied to form a number
   1. Write down the number formed                                                                         (2 marks)
   2. State the total value of the second digit in the number formed                          (1 mark)
3. An arc of a circle subtends an angle of 60° at the centre .Find the length of the arc if the radius of the circle is  42cm (Take π = ²²/₇)     (3 marks)
4. Evaluate;                          (3 marks)
   −7×−1(3 of−¹/₃ − 4) ÷ 5+−2
           8÷4×-2+ -7
5. A square based copper plate is 14cm high and has a mass of 8.4kg. The density of the copper is 6.0 g/cm³ .Calculate the length of the plate         (3 marks)
6. Given  that x = −2, find the values of y and z for the simultaneous equations        (4 marks)
   x + y − z = −1
   x − 2y + z = −7
7. Without using a calculator, simplify                   (3 marks)
     2¹/₃ − 1²/₃ + 1¹/₃ 
      ³/₇ of 3²/₃ − 3⁴/₇
8. A prism of length 4cm has a cross section of an equilateral triangle of sides 3cm .Draw an accurate net of the prism below           (3 marks)
   
9. Find the greatest number which when divided by 247, 367 and 607 leaves a remainder of 7 in each case.                         (3 marks)
10. Given that 2x² + 3.824² = √358.3 , use the tables of squares and square roots to find the value of x .                     (4 marks)
11. A cube has a surface area of  216cm² calculate its volume                                     (3 marks)
12. A football match first half takes 45 minutes. In a given day the match started at 9.15 a.m. after 15 minutes the game was interrupted by rains and stopped for 30 minutes. At what time did the first half end?                            (2 marks)
13. Kenyan company received US Dollars 195 000. The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows; 
    

    Currencies	Buying Ksh	Selling Ksh
    1 US dollar	78.25	79.45
    1 sterling pound	122.94	123.28

    1. Calculate the amount of money in Kenya shillings the company received.           (1 mark)
    2. The company converted all the Kenya shillings calculated in (a) above into Sterling pounds to buy a car from Britain valued at the same amount. They allowed a discount of 5% on the value of the car. Calculate the buying price of the car to the nearest sterling pound. (2 marks)
14. Find the sum of the interior angles of a regular hexagon                                             (3 marks)
15. Without using a set square or a protractor construct:
    1. Triangle ABC such that AB = 8cm, BC = 6cm and ∠ABC=30°                (3 marks)
    2. Measure the length AC.                    (1 mark)
16. Given that a=3,b=5 and c = −½ , evaluate                                                         (3 marks)
      ¼(b² − 3a)     
    4a² + 2b − 4c

SECTION II (50 Marks)      
Answer all questions in this section

1.  
   1. A trader sold an article at Sh. 4800 after allowing his customer a 12 % discount on the marked price of the article .In so doing he made a profit of 45% calculate
      1. The marked price of the article                       (2 marks)
      2. The price at which the trader had bought the article                                        (2 marks)
   2. Calculate the percentage profit the trader would have made if he had sold the same article without giving a discount to 2 decimal places        (2 marks)
   3. Joan is a sales executive earning a salary of Ksh 20000 and a commission of 8% for the sales above Sh. 100 000. If in April 2018 she earned a total of Sh. 48 000 in salaries and commissions, determine the amount of sales she made in that month.          (4 marks)
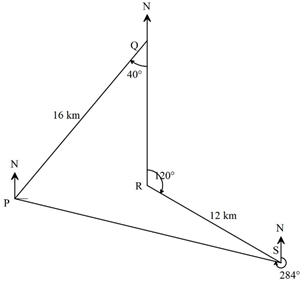
2. The boundaries PQ, QR, RS and SP of a ranch are straight such that: Q is 16 km on bearing of 040° from P; R is directly south of Q and east of P and S is 12 km on a bearing 120° from R.
   1. Using a scale 1 cm represent 2 km, show the above information in a scale drawing.              (3 marks)
   2. From the scale drawing determine
      1. The distance in kilometres of P from S.       (2 marks)
      2. The bearing of P from S.                   (2 marks)
      3. Calculate the area of the ranch PQRS in square kilometres.                          (3 marks)
3.  Two alloys A and B, are each made up of copper, zinc and tin. In alloy A the ratio of copper to zinc is 3:2 and the ratio of zinc to tin is 3:5.
   1. Determine the ratio, copper∶ zinc∶ tin in alloy A.             (2 marks)
   2. The mass of alloy A is 250??. Alloy B has the same mass as alloy A but the amount of copper is 30% less than that of alloy A , calculate
      1. The mass of tin in alloy A.                                                                         (2 marks)
      2. The total mass of zinc and tin in alloy B.                                                   (3 marks)
   3. Given that the ratio of zinc to tin in alloy B is 3:8. Determine the amount of tin in alloy B than in alloy A.                       (3 marks)
4.  
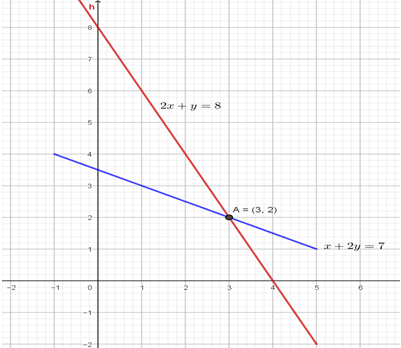
   1. Complete the tables below for the following equations                                      (4 marks)
      

      2x + y = 8
      x	0	1	2	3	4
      y			4		0

      
      

      x + 2y = 7
      x	0	1	2	3	4
      y	3.5			2

   2. Draw the graph of 2x+y =8 and x+2y=7 on the same axis                       (3 marks)
   3. Use your graph to solve the simultaneous equation 2x + y=8 ,x+2y =7   (1 mark)
   4. The line 2x + y = 8 meets the x-axis at a point R .Write down the coordinates of point R                           (1 mark)
   5. The line x+ 2y =7 meet the y – axis at point P .Write down the coordinates of Point P                (1 mark)
5.  
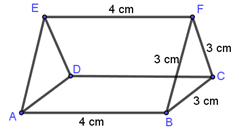
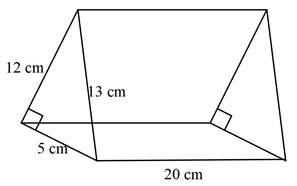
   1. Find the surface area of a triangular prism shown.                                                  (8 marks)
      
   2. If John was go round the prism calculate the total distance he would cover.          (2 marks)

MARKING SCHEME

No.	Working	Remarks
1	12 mg = 0.012g  Total mass = 15 + 0.012 = 15.012 g ⟹ 1.5012 × 10−2kg	M1  A1  B1
2	⟹1×3×5×7×9  = 945 4 × 10 = 40	M1  A1  B1
3	l = θ/360 × 2πr l = 60/360 × 2 × 22/7 × 42   = 44 cm	B1  M1  A1
4	N⟹ −7 × −1(3 × −1/3 − 4) ÷ 5 + −2     = 7(−5) ÷ 5 − 2     =4 D⟹ 8 ÷ 4 −2+ −7      = 2 × − 2 − 7      = −11 N/D ⟹ −4/11	M1  M1   A1
5	V = 8400 = 1400 cm3           6  V=l2 × h 1400 = l2 × 14  l2 = 1400  = 100          14 l = √100 = 10 cm	M1  M1  A1
6	y − z = 1 ......... (i) −2y + z = −5 ..(ii) −2(1+z) + z = −5 −2 − 2z + z = −5 −z = −3  z = 3 y = 1 + 3 = 4	M2- both eqns M1 A1 both values
7	N ⟹ 21/3 − 12/3 + 11/3     =  7 − 5 + 4               3      = 2 D ⟹ 3/7 × 11/3 − 25/7      =  11/7 − 25/7      = −2 N/D ⟹ 2 ÷ −2 = −1	M1  M1   A1
8		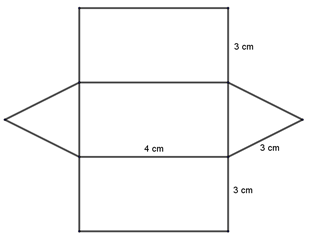B1 – correct lengths B1 – correct shape B1 – complete diagram
9	247 − 7 = 240 367 − 7 = 360  607 − 7 = 600 240 = 24 × 3 × 5 300 = 23 × 32 × 5 600 = 23 × 3 × 52 GCD of 240, 360 and 600 ⟹ 23 × 3 × 5 = 120	M1  M1  A1
10	3.8242 = 14.623 √(3.583 × 10−2) = 18.929 2x2 = 18.929 − 14.623  2x2 = 4.306  x2  = 2.153 x = √2.153 = 1.4673	B1 – both values from tables M1   A1
11	Area of 1 face = 216/6 = 36cm2 Length = √36=6 cm Volume = 36 × 6 =216 cm3	M1  M1  A1
12	Total time taken = 30 mins + 45 mins = 1 hr 15 mins 1st half ends at = 9.15 a.m + 1 hr 15 mins = 10.30 a.m	B1  B1
13	195 000 × 78.25 = Ksh.15 258 750 Amount in sterling pounds  = 15 258 750 = 123 773                                                   123.28            Buying price of the car = 95/100 × 123 773 = 117 584 pounds	M1    M1  A1
14	Hexagon = 6 sides Sum = (2n−4)90 = (12−4)90 = 720°	B1  M1  A1
15	AC = 4.1 ± 0.1 cm	B1 – lines AB, BC B1 - ∠ABC B1 – complete diagram B1
16	N⟹¼ (25 − 9) = ¼ × 16 = 4 D⟹4(32) + 2(5) −4 (−½) = 36 + 10 + 2 = 48 N/D ⟹ 4/48 = 1/12	M1  M1  A1
17	Marked price = 100 × 4800 = Sh.5 454.50                                  88 Buying price = 100 ×4800 = Sh.3310.30                               145 Profit = 5454.50 − 3310.30 = Sh.2144.20 Percentage profit = 2144.20  × 100 = Sh.64.7%                                3310.30 Commission  = 48 000 − 20 000 = Sh.28 000 Sales earning commission = 100 × 28 000 = Sh.350 000                                                 8 Total sales = 100 000 + 350 000 = Sh.450 000	M1 A1 M1 A1 M1 M1 A1 M1 M1  M1 A1
18	PS = 10.6 ± 0.1       = 21.2 km Bearing of P from S = 284 ± 2° Area of the ranch =	B1 – bearing at P   B1 – bearing of R from Q B1 – length PR   M1 A1 B1 B1
19	Copper  Zinc   Tin      3   2     x3    3  5   x2  9  6  10   The ratio of copper : Zinc : Tin = 9:6:10   Mass of tin = 10/25 × 250 = 100 kg Copper in B = 70/100 × 9/25 × 250 = 63 kg Mass of tin and zinc = 250 − 63 = 187 k Tin in B = 8/11 × 187 = 136 kg Tin in A = 100 kg Difference = 136 − 100 = 36 kg	B1 – for relating ratios   B1 M1 A1   M1  M1 A1 M1   M1 A1
20	2x + y = 8                   x + 2y = 7   x  0  1   2   3   4   0  1   2  3  4  y  8  6  4  2  0  3.5  3  2.5 2  1.5   Coordinates of point of intersection A (3, 2) Coordinates of R (4,0) Coordinates of P (0,3.5)	B2 – table 1 B2 – table 2 B1 – axis and scale B1 – plotting B1 – both lines             B1 B1 B1
21	Area of triangular faces = 2(½ × 5 × 12) = 2 × 30 = 60cm2 Area of rectangular faces 20 × 13 = 260cm2  20 × 5 = 100cm2 20 × 12 = 240cm2 Total area of triangular faces = 260 + 100 + 240 = 600cm2 Total surface area = 600 + 60 = 660cm2 Total distance covered = 2(20+13+13+12+12)                                      = 2 × 70 = 140 cm	M1 A1   M1 M1 M1 M1 M1 A1   M1 A1