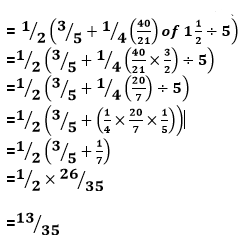SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.
- Evaluate: (3mks)
1/2(3/5 + 1/4 (7/3 − 3/7) of 11/2 ÷5) - A triangle has vertices A(2,5), B(1,-2) and C(-5,1). Determine;
- The equation of line BC. (2mks)
- The equation of perpendicular line from A to BC. (2mks)
- The shaded region in the figure below shows an area swept out on a flat windscreen by a wiper.
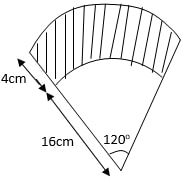
Calculate the area of the region. Take π= 3.142. (3mks) - A piece of metal has a volume of 20cm3 and a mass of 300g. Calculate the density of the metal in kg/m3. (3mks
- List the integral values of x which satisfy the inequalities below. (3mks)
2x + 21 > 15 − 2x ≥ x + 6 - Janet is a saleslady earning a basic salary of Kshs. 20,000 per month and a commission of 8% for the sales in excess of Kshs. 100,000. If in January 2010 she earned a total of Kshs. 48,000 in salaries and commissions. Determine the amount of sales. She made in that month. ` (3mks)
- The interior angle of a regular polygon is 108o larger than the exterior angle. Find the number of sides of the polygon. (3mks)
- Given that Cos A = 5/13 and angle A is acute. Find the value of 2tan A + 3sin A without calculators. (3mks
- Without using a calculator evaluate: (2mks)
(−9 + (−7) × (−8) − (−5)
(−2 + (−6) ÷ 3 × 6) - Solve for x in the equation below. (3mks)
(6x − 4) − (2x − 1) = (6 − 5x)
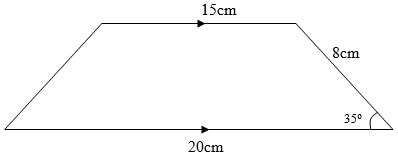
3 2 6 - Calculate the area of the trapezium show below. (3mks)
- Solve the simultaneous equation. (4mks)
x2 + y2 = 26
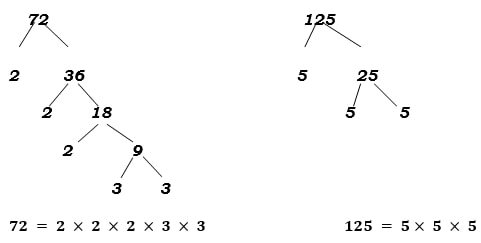
x + y = 4 - Express 72 and 125 as products of their prime factors. (2mks
- A service vehicle left town P for town Q at 1000 hrs had a puncture after travelling for 4 hrs 20 mins. Fixing a new tyre took 33 minutes. The vehicle then travelled for 1 hr 20mins to reach town Q. At what time did it arrive in 12 hour clock system? (3mks)
- A tourist visited Kenya with 2500 US dollars and changed the US dollars into Kenya shillings at a local bank in Kenya when the exchange rates at the time were as follows:
Buying Selling
1 US dollar shs.78.45 shs. 78.55
1 Sterling Pound shs.120.25 shs. 120.45- How much did he get in Kenya shillings? (2mks)
- While in Kenya he used shs. 80,000 and after his stay he converted the remaining amount into Sterling pounds. Calculate to 2 decimal places the Sterling pounds that he got. (2mks)
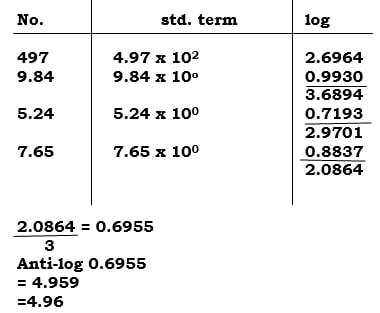
- Use logarithms tables to evaluate: (4mks)
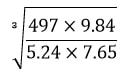
SECTION II (50 marks)
Answer any five questions in this section in the spaces provided.
- A motorist left Embu for Nairobi a distance of 240km at 8:00 a.m. and travelled at average speed of 90km/hr. Another motorist left Nairobi for Embu at 8:30a.m and travelled at 100km/hr. Find;
- The time they met. (3mks)
- How far they met from Nairobi. (3mks)
- The time of the day each motorist arrived at his destination. (4mks)
- A farmer has a rectangular farm which measures 100m by 80m. The farmer intends to fence the plot using post at intervals of 4m apart leaving a gate of 4m. Also he will use four strands of barbed wire. Each post cost shs. 125 and wire is sold at rolls of 60m costing shs. 1,500. Calculate;
- The number of post he will use. (2mks)
- The total length of the barbed wire. (2mks)
- The total cost of fencing the farm if the cost of the gate is 8,000/= and labour is shs. 1,500. (3mks)
- The farmer wishes to subdivide further the farm into square plot. Find the maximum area of each plot. (2mks
- The parents of a certain mixed school decided to buy a school van worth Kshs 900,000. Each student was to contribute the same amount of money. 50 students were transferred from the school as a result each of the remaining students had to pay kshs.600 more.
- Find the original number of the students in the school. (5mks)
- Find the percentage change in contributions per student. (3mks)
- If the ratio of boys to girls in the school was 11:7, find the amount of money contributed by boys alone. (2mks)
- The figure below shows two circles of radii 8cm and 6cm with centres O1 and O2 respectively. The circles intersect at points A and B. The lines O1O2 and AB are perpendicular to each other. If the common chord is 9cm; (Take π=3.142.
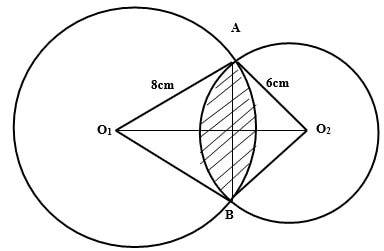
Calculate to 4.s.f.- Angle AO1B (2mks)
- Angle AO2B (2mks)
- Area of the shaded region. (6mks)
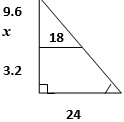
- A village water tank is in the form of a frustum of a cone of height 3.2m. The top and bottom radii of 18m and 24m respectively as shown below.
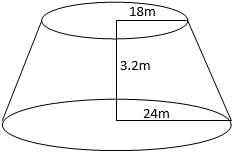
- Calculate;
- The surface area of the tank excluding the bottom. (4mks)
- The capacity of the tank in litres. (3mks)
- 15 families each having 15 members use the water tank and each person uses 65 litres daily. How long will it take for the full tank to be emptied? (3mks)
- Calculate;
- Measurements of a maize field using baseline XY were recorded as shown below in metres

- Show the map of the maize field by scale drawing. Take 1cm rep 20m. (4mks)
- Find the area of the field in hectares. (4mks)
- If the cost of one hectare is Kshs. 65,000, find the total cost of the maize field. (2mks)
- Using a ruler and pair of compass only construct the following.
- Triangle XYZ where XY is 6cm and angle XYZ is 135o and YZ = 7 cm. Measure XZ. (3mks)
- Drop a perpendicular from Z to meet line XY at K. measure YK. (3mks)
- Bisect line XY and let the bisector meet line XZ at Q. (2mks)
- Join Q to Y and measure angle XQY. (2mks)
- Complete the table for the function.
- y=1 – 2x – 3x2 in the range -3 ≤ x ≤ 3 (2mks)
x −3 −2 −1 0 1 2 3 −3x2 −27 −3 0 −12 −2x 0 −6 1 1 1 1 1 1 1 1 y −20 1 −15 - Use the table above to draw a graph of y=1 – 2x – 3x2 on the graph provided. (4mks)

- Use the graph in (b) above to solve;
- 1 – 2x – 3x2 = 0 (2mks)
- 2 – 5x – 3x2 = 0 (2mks)
- y=1 – 2x – 3x2 in the range -3 ≤ x ≤ 3 (2mks)







Marking Scheme
-
-
- B (1, −2) C(−5, 1)
Gradient = (1− −2)
(−5 −1)
=−3/6 =−1/2
B (1, −2) (x, y)
= (y+2) = −1
(x−1) 2
y + 2 = 1⁄2x+ 1⁄2
y = 1⁄2 x+ -3⁄ - A (2,5) G = 2
= (y − 5) =2
(x − 2)
y – 5 = 2x – 4
y = 2x + 1
- B (1, −2) C(−5, 1)
- 3.142 ×120/360×202 − 3.142 × 120/360 × 162
418.93 – 268.12
= 150.81cm2 - D = mass
volume
= 20/300 ×1000
= 66.67 kg/m3 - 2x + 21 > 15 – 2x 15 – 2x ≥ x + 6
4x > -6 9 ≥ 3x
x > -1.5 3 ≥ x
-1.5 < x ≤ 3
Integral values -1, 0, 1, 2, 3 - 48,000 – 20,000 = 28,000/=
28000 = 8/100 × x
x = 350,000 + 100,000 - x + (x + 108) = 180
2x + 108 = 180
x = 36
Interior = 36 + 108 = 144
Exterior = 36o
No. of sides = 360/36
= 10 sides. -
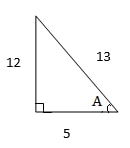
2(12/5) + 3(12/13)
24/5 + 36/13
= 492/65 - N = -9+56+5
= 52
D = -2 + (-2) ×6
= -14
= 52/-14 = -26/7
= -3 5/7 -
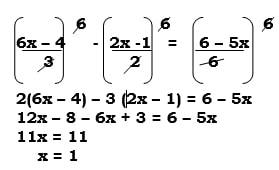
- A = ½ x (15+20) ×8 sin 35
= 80.3 cm2 - x = 4 – y
(4 - y)2 + y2 = 26
16 – 8y + y2 + y2 = 26
2y2 – 8y – 10 = 0
y2 – 4y – 5 = 0
y = -1 x = 5
y = 5 x = -1 -
- 10 00 hrs
+4 20
14 20 hrs
+33
14 53
1 20
16 13h
= 4:13p.m -
- 2500 x 78.45
= shs. 196125 - 196125
-80000
116125
116125
120.45
= 964.09 sterling pounds
- 2500 x 78.45
-
-
-
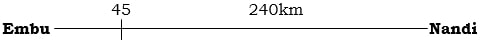
8: 00 am → 90km/h
T= 30mins
S= 90km/h
D= 45km
D.A = 195km
RS = 190km/hr
T = 39/38
8.30 am
+62
9.32 am - T= 39/38 hr
S = 100km/hr
D= 102.63 km - Embu → Nairobi Nairobi → Embu
D = 240km D = 240km
S = 90km/hr S = 100km/hr
T= 2hr 40mins T = 2h 24mins
8.00 8.30
2.40 2.24
10.40am 10.54 am
-
-
- P = 180 × 2
= (360-4) = 89+1
4
= 90 posts - (360 – 4) ×4
= 1424 m - (90 x 125) + (1424 x 1500) + 8000
60
11250 + 35600 + 8000 + 1500
= sh. 56350 -
G.C.D = 2010 100 80 2 10 8 5 4
Area= 20 × 20
= 400m2
- P = 180 × 2
- 900000 − 900000 = 600
(x – 50) x
900000x – 9000000x + 45000000 = 600
x (x -50)
45000000 = 600x2 – 30000 x
600x2 – 30000x – 45000000 = 0
x2 – 50x – 75000 = 0
50 ± √(2500- 4 x 75000)
2
50 + 550 50 - 550
2 2
x = 300 students - Original = 900000
300
= 3000
New = 900000
250 - = 3600
= 600 x 100
3000
= 20% - B G
11 7
= 11 x 900000
18
= sh. 55,000
- 900000 − 900000 = 600
-
- Angle AO1B (2mks)
Sin-1θ=(4.5/8)
θ=34.23
AO1B = 34.23 ×2
= 68.46o - Angle AO2B
Sin-1θ=4.5/6
θ=48.59
AO2B = 48.59 × 2
= 97.18o - Area of the shaded region. (6mks)
68.46/360 × 3.142×82 − 1⁄2×8×8 Sin 68.46
38.24 − 29.76
= 8.48cm2
97.18/360 × 3.142×62 − 1⁄2 × 6 × 6 Sin 97.18
30.53 − 17.86
= 12.67
Shaded Area = 8.48 + 12.67
= 21.15 cm2
- Angle AO1B (2mks)
-
-
- The surface area of the tank excluding the bottom. (4mks)
24 = 3.2 + x
18 x
24x = 57.6 + 18x
6x = 57.6
x = 9.6m
slant height of big cone = √(242 + (9.6+3.2)2)
= 27.2
S.A Big Cone = 22/7 × 24×27.2
= 2051.66cm2
S.A of small Cone = 22/7 × 18 × 20.4
= 1154.06
S.A of tank =2051.66 – 1154.06 + 22/7 × 182
= 897.6 + 1018.29
= 1915.89 m2 - The capacity of the tank in litres. (3mks)
Volume of big cone =1⁄3×22/7×24×24×12.8
= 7723.89 m3
Volume of small cone =1⁄3×22/7×18×18×9.6
= 3258.51m3
Volume of tank = 7723.89 − 3258.51
= 4465.3757
4465.3757 ×1000
= 4465375.7 litres
- The surface area of the tank excluding the bottom. (4mks)
- (4465375.7)
(15×15×65)
= 305.3 days.
-
-
- Show the map of the maize field by scale drawing. Take 1cm rep 20m. (4mks)
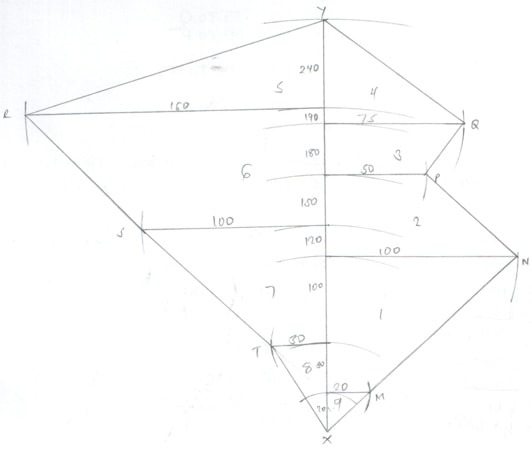
1. A = ½ (a + b)h
= ½ (20 +100)80
= 4800 m2
2. A = ½ (a + b ) h
= ½ (20 + 100)60
= 4500m2
3. A = ½ (a +b)h
= ½ (50 +75 ) 40
= 2500m2
4. A= ½ bh
= ½ x 75 x 60
= 2250m2
5. A = ½ bh
= ½ x 160 x 50
= 4000m2
6. A = ½ (a + b)h
= ½ ( 100 + 160) 70
= 4550 m2
7. A = ½ bh
= ½ x 30 x 50
= 750
8. A = ½ bh
= ½ x 20 x 20
= 200m2 - Find the area of the field in hectares. (4mks)
= 4800 + 4500 + 2500 + 2250 + 4000 + 5600 + 4550 + 750 + 200
= 29150m2
1 ha = 10, 000 m2
? = 29, 150 m2
= 29150 x 1
10000
= 2.9150ha - If the cost of one hectare is Kshs. 65,000, find the total cost of the maize field. (2mks)
1 ha = shs 5000
2.9150 ha = ?
= 2.9150 x 65000
1
= ksh. 189475
- Show the map of the maize field by scale drawing. Take 1cm rep 20m. (4mks)
-
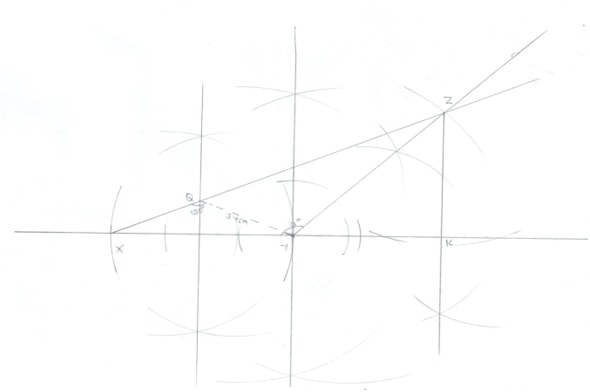
- measure YK. (3mks)
= 4.8 cm - Bisect line XY and let the bisector meet line XZ at Q. (2mks)
- Join Q to Y and measure angle XQY. (2mks)
XQY = 130o
- measure YK. (3mks)
- Complete the table for the function.
-
x −3 −2 −1 0 1 2 3 −3x2 −27 -12 −3 0 -3 −12 -27 −2x 6 4 2 0 -2 -4 −6 1 1 1 1 1 1 1 1 y −20 -7 0 1 -4 −15 -32 - Use the table above to draw a graph of y=1 – 2x – 3x2 on the graph provided. (4mks)
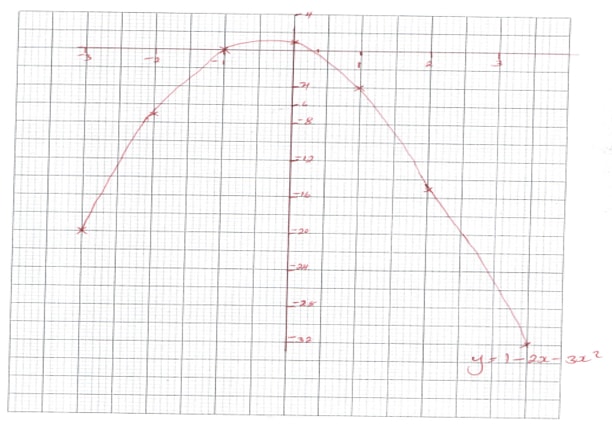
- Use the graph in (b) above to solve;
- y=1 – 2x – 3x2 = 0 (2mks)
1 – 2x – 3x2=0
= -1, 0.2 - 2 – 5x – 3x2 = 0 (2mks)
1 - 2x – 3x2 = 0
2 - 5x – 3x2 = 0
-1 + 3x = 0
3x = 1
x = 1/3
- y=1 – 2x – 3x2 = 0 (2mks)
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 - Form 3 End Term 2 Exams 2021 Questions and Answers.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students