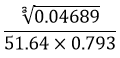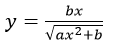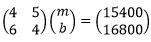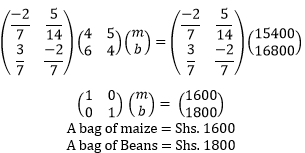Mathematics Paper 2 Form 3 End Term 2 Exams 2021 with Marking Schemes

SECTION I (50MARKS)

Answer all questions in this section

1. Evaluate using logarithms. [4 Marks]
   
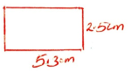
2. A rectangular card measures 5.3 cm by 2.5cm.Find 
   1. The absolute Error in the area of the card. [2 Marks]
   2. The Percentage Error in the area of the card [2 Marks]
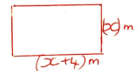
3. The length of a room is 4m longer than its width. Find the length of the room if its area is 32m². [3 Marks
4. If 20 Men can lay 36m of a pipe in 8 hours. How long would 25 Men take to lay the next 54m of the pipe? [2 Marks]
5. Expand (2 + x)⁵ in ascending powers of x up to the term in x³. Hence, approximate the value of (2.03)⁵ to 4s.f. (4 marks)
6. Simplify by rationalizing the denominator; [2 Marks]
           3       
   2√3 − √2
7. A scientific calculator is marked at sh. 1560. Under hire purchase it is available for a downpayment of sh. 200 and six monthly instalments of sh. 250 each. Calculate;
   1. The Hire purchase price. [2 Marks]
   2. The extra amount paid out over the cash price. [1 Mark]
8. Solve the equation; [3 Marks]
   log⁡ (2x − 10) − 2 log 8 = 2 + log⁡ (9 − 2x)
9. The Equation of a circle is given by x² + y² − 6x + 4y − 3 = 0 . Determine the center and the radius of the circle. [3 Marks]
10. Make x the subject of the formula in the equation. [3 marks]
    
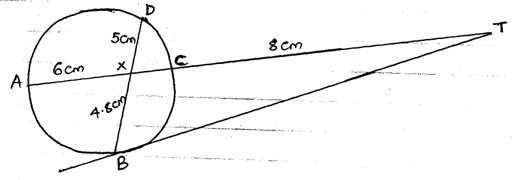
11. In the figure below, BT is a tangent to the circle to the circle at B. AXCT and BXD are straight lines. AX=6cm, CT=8cm, BX=4.8cm and XD=5cm.
    
    Find the length of;
    1. XC [2 Marks]
    2. BT [2 Marks]
12. Find the value of x if the matrix is a singular matrix. [3 Marks]
13. The first term of an arithmetic sequence is −7 and the common difference is 4.
    1. List the first 6 terms of the sequence [2 Marks]
    2. Determine the sum of the first 30 terms of the sequence [2 Marks]
14. The coordinates of points A and B are (2,5) and (8, −7) respectively. Find the
    1. Coordinates of M Which Divides AB in the Ratio 1:2 [2 Marks]
    2. Magnitude of AB [2 Marks]
15. Tap A Fills a tank in 6 hours, tap B fills it in 8 hours and tap C empties it in 10 hours.Starting with an empty tank and all the three taps are opened at the same time, how long will it take to fill the tank. [3 Marks]
16. Grade X of Tobacco Costs Sh.81.50 per Kg and grade Y cost sh 109 per Kilogram. In what ratio must the two grades be mixed in order to make a profit of 20% when the mixture sells at sh. 112.80 per kg. [3 Marks]

SECTION II: (50MARKS)

Answer any 5 questions from this section

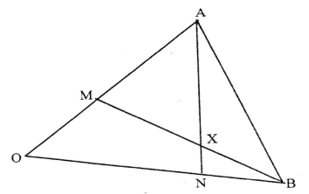
17. The figure below shows triangle OAB in which M divides OA in the ratio 2: 3 and N divides OB .in the ratio 4:1 AN and BM intersect at X.
    
    
    1. Given that OA = a and OB = b, express in terms of a and b: (4mks)
       1. AN
       2. BM
    2. If AX = sAN and BX = tBM, where s and t are constants, write two expressions for OX in terms of.a, b s and t. Find the value of s and t. Hence write OX in terms of a and b (6mks)
18. Kamau, Njoroge and Kariuki are practicing archery. The probability for Kamau hitting the target is ²/₅ , that of Njoroge hitting the target is ¹/₄ and that of Kariuki hitting the target is ³/₇. 
    Find the probability that in one attempt;
    1. Only one hits the target (2mks)
    2. All three hit the target (2mks)
    3. None of them hits the target (2mks)
    4. Two hit the target (2mks)
    5. At least one hits the target (2mks)
19.  
    1. A matrix T is given by . Find T^-1 [2 Marks]
    2. Wanjiku bought 20 bags of maize and 25 bags of beans at a total cost of sh. 77,000. If she had bought 30 bags of maize and 20 bags of beans, she would have spent sh. 7,000 more. 
       1. Form a matrix equation from this information. [1 Mark]
       2. Determine the cost of a bag of maize and a bag of beans. [3 Marks
    3. She sold all the maize and beans at a profit of 10% on a bag of maize and 12½ % on a bag of beans. Calculate the total percentage profit. [4 Marks]
20. At the beginning of the year 2000, Kanyora bought two houses, one in Thika and the other in Nakuru each at 1,240,000. The value of the house in Thika appreciated at a rate of 12% p.a.
    1. Calculate the value of the house in Thika after 9 years to the nearest shilling. [2 Marks
    2. After n years, the value of the house in Thika was 2,741,245 while the value of the house in Nakuru was 2,917,231. 
       1. Find n [4 Marks]
       2. Find the annual rate of appreciation of the house in Nakuru. [4 Marks]
21. The table below shows income tax rates. 
    

    Taxable income   K£ per month	Rate in shs. per K£
    1 - 325	2
    326 - 650	3
    651 - 975	4
    976 - 1300	5
    1301 - 1625	6
    over 1626	7

    Mr. Wafula earns a basic salary of 30,500. He has a house allowance of sh. 6,000 per month, medical allowance of sh. 4,000 per month and transport allowance of sh. 3,000 per month. He claims a tax relief of sh. 1,056 per month.
    1. Calculate
       1. Wafula’s taxable income in k£ per month. [2 Marks]
       2. Gross tax. [3 Marks]
       3. Net Tax [2 Marks]
    2. His net income per month has the following deductions
       
       Health insurance fund – sh. 150 
       Loan interest – sh. 200
       Service charge – sh. 200
       Sacco loan – sh. 2,500
       
       Calculate his net income per month. [3 Marks]
22.  
    1. P varies jointly as Q and the square of R. P = 18 when Q = 9 and R = 15. Find R when P=32 and Q=81. [5 Marks]
    2. A varies Directly as B and inversely as the square root of C. Find the percentage change in A When B is decreased by 10% and C increased by 21%. [5 Marks]
23.  
    1. The first term of an arithmetic progression is 2. The sum of the first 8 terms of the AP is 240.
       1. Find the common difference of the AP. [2 Marks]
       2. Given that the sum of the first n terms of the AP is 1,560. Find n [2 Marks]
    2. The 3rd, 5th and 8th terms of another AP from the first three terms of a G.P. If the common difference of the AP is 3. Find.
       1. The first term of G. P [4 Marks]
       2. The sum of the first 9 terms of the G.P to 4 s.f. [2 Marks]
          
          
24.  
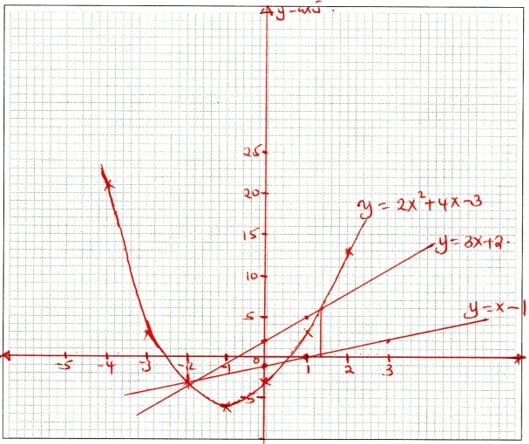
    1. Complete the table below for the function Y=2x² + 4x − 3 [2 Marks]
       

       x	−4	−3	−2	−1	0	1	2
       2x2	32			1	0		8
       4x	−8	−12	−8			4	8
       −3	−3	−3	−3	−3	−3	−3	−3
       y	21		−3

    2. On the grid provided, draw the graph of the function y=2x² + 4x − 3for −4 ≤ x ≤2 [3 Marks]
       
    3. Use your graph to solve the roots of the quadratic equations.
       1. 2x² + x − 5 = 0 [2 Marks]
       2. 2x²+3x − 2 = 0 [2 Marks]
       3. x² + 4x − 3 = 0 (1 mark)

 

 

 

Marking Scheme

1.   
   
2.  
   1.  
      
      

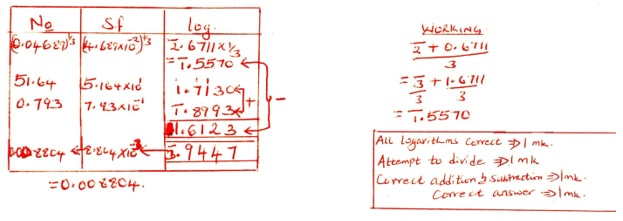
      Minimum	Actual	Maximum
      5.25	5.3	5.35
      2.45	2.5	2.55

      
      Max. Area = 5.35 × 2.55
                      = 13.46 cm²
      Min. Area = 5.25 × 2.45
                     = 12.8625 cm²
      Absolute Error = max − min
                                      2
                           = 13.6425 − 12.8025 = 0.78 ✓1
                                           2
      
      
   2. % error = Absolute error × 100 âœ“1
                      Actual area
                   =    0.78      × 100
                      5.3 × 2.5
                   = 5.8868 % âœ“1
3.  
   
   x(x+4) = 32
   x² + 4x − 32 = 0
   x² + 8x − 4x − 32 = 0
   x (x+4) − 4(x+8) = 0
   (x − 4)(x+8) = 0
   x = 4 or x = -8
   ∴ x =4 since length can't be negative
   length = x + 4 = 4+4 = 8m 
4. Men Length Hours
   20    36       8
   25    54       ?
   = ²⁵/₂₀ × ⁵⁴/₃₆ × 8 âœ“1
   = 15 hours âœ“1
5. (2+x)⁵
   

   Co-efficients	1	5	10	10	5	1
   Expansion	25x0	24x1	23x2	22x3	21x4	20x5
   Combined	32	80x	80x2	40x3	10x4	x5

   = 32 + 80x + 80x² + 40x³ 
   (2+x)⁵ = 2.03⁵
   2+x = 2.03
       x = 2.03 − 2
       x = 0.03
   ∴ 2.03⁵ = 32 + 80 (0.03) + 80 (0.03)² + 40 (0.03)³
               = 32 + 2.4 + 0.072 + 0.00108 
               = 34.47308 ≈ 34.47 âœ“1
6.  
   
7.  
   
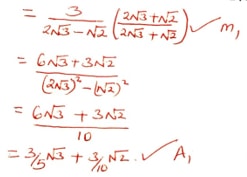
   1. = 200 + (2500 × 6)
      = sh. 1700
   2. 1700 − 1560
      = sh. 140 
8. log (2x − 10) = log (100 × (9 − 2x) )
   2x − 10 = 900 − 200x
      64                1
   2x − 10 = 57600 − 12800x
   12802x = 57610
   x = 57610
         12802
       = 4.5001
       ≈ 4.5
   
   
9. (x² − 6x + ___) + (y² + 4y + ___) = 3 + ___+ ___
   x² − 6x + ⁶/₂ + y² + 4y + ⁴/₂ = 3 + (⁶/₂) + (⁴/₂)²
   (x − 3)² + (y+2)² = 16
   = centre (3, −2)
   = Radius = √16
                 = 4 units
10.  
    
11.  
    1. 6 (XC) = 4.8 × 5
       XC = 4.8 × 5
                    6
             = 4 cm
    2. BT² = AT.CT
             = 18 × 8 
       BT = √144
           = 12 cm
12. For singular matrix det = 0 
    ∴ {x(x − 3)} − (4 × 1) = 0
    x² − 3x − 4 = 0
    x² + x − 4x − 4 = 0
    x(x+1) − 4(x+1) = 0
    (x−4) (x+1) = 0
    x = −1 or 4
13.  
    1. 1^st term = −7
       2^nd term = −7 + 4 = −3
       3^rd term = −3 + 4 = 1
       4^th term = 1 + 4 = 5
       5^th term = 5 + 4 = 9
       6^th term = 9 + 4 = 13
    2. S₃₀ = ³⁰/₂{2(−7) + (30 − 1)4}
             = 15 {−14+116}
             = 1530
       
       
14.  
    
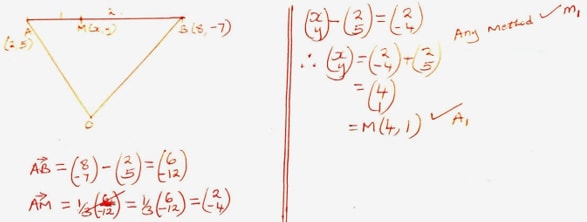
15. Tap A ⇒ 6 hours
    in 1hr = ¹/₆ of the tank
    Tap B ⇒ 8 hours
    in 1hr = ¹/₈ of the tank
    in 1hr both = ¹/₆ + ¹/₈
    Tap C ⇒ 10 hours to empty
    in 1hr = ¹/₁₀
    All three in hour = 7 − 1 = 35 − 12 =  23 
                              24   10      120        120
    ²³/₂₀ = 1 hr
    1       = ?
    1 × 1 × ¹²⁰/₂₃
    = 5.22 hours
    = 5 hrs 13 min
16.           Grade X    Grade Y    Mixture
    B.P     sh 81.50   sh. 109
    Ratio        x     :     y
    Total     81.50x      109y     81.50x + 109y
    ¹²⁰/₁₀₀(81.50x + 109y) = 112.80
                      x + y
    97.8x + 130.8y = 112.80x + 112.80y
    97.8x − 112.80x = 112.80y − 130.8y
    −15x = −18y
    x = 18 ⇒ x:y = 6:5
    y    15
17.  
    1.  
       1. AN = AO + ON
               = −a + ⁴/₅b
       2. BM = BO + OM
               = −b + ²/₅a
    2. OX = OA + AX
            =  a   + sAN
            = a + s (⁴/₅b − a) 
            = a − sa + ⁴/₅sb
            = a(1 − s) + ⁴/₅sb
       Also:
       OX = OB + BX
            = b + t BM
            = b + t(²/₅a − b)
            = b − tb +²/₅ta
            = b (1 − t) + ²/₅ta
       
       a(1 − s) + ⁴/₅sb  = b (1 − t) + ²/₅ta
       1 − s = ²/₅ta 
       t = ⁵/₂ − ⁵/₂s ------- (i)
       
       ⁴/₅s = (1 − t) --------(ii)
       ⁴/₅s = 1 − (⁵/₂  − ⁵/₂s)
       ⁴/₅s = 1 − ⁵/₂ + ⁵/₂s
       ⁴/₅s =  − ³/₂  + ⁵/₂s
       ³/₂ = ¹⁷/₁₀s
       s = ¹⁵/₁₇
       t = ⁵/₂ − ⁵/₂s
       t = ⁵/₂ − ⁵/₂ × ¹⁵/₁₇
       t = ⁵/₁₇
       ∴ OX = b(1 − ⁵/₁₇) + (²/₅ × ⁵/₁₇)a
       = ¹²/₁₇b + ²/₁₇a
18.  
    1. (²/₅ × ³/₄ × ⁴/₇) + (³/₅ × ¹/₄ × ⁴/₇) + (³/₅ × ³/₄ × ³/₇)
       = ⁶/₃₅ + ³/₃₅ + ²⁷/₁₄₀
       = ⁹/₂₀
    2. P(HHH) = ²/₅ × ¹/₄ × ³/₇
       = ³/₇₀
    3. P('H'H'H) = ³/₅ × ³/₄ × ⁴/₇
       = ⁹/₃₅
    4. (²/₅ × ¹/₄ × ⁴/₇) + (²/₅ × ³/₄ × ³/₇) + (³/₅ + ¹/₄ + ³/₇)
       = ²/₃₅ + ⁹/₇₀ + ⁹/₁₄₀ = ¹/₄
    5. P(1 or 2 or 3) = 1 − (P(none hits))
                            = 1 − ⁹/₃₅
                            = ²⁶/₃₅
19.  
    1.  
       
    2.  
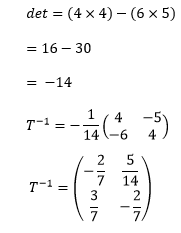
       1. 4         5       15400
          20m + 25b = 77000
          30m + 20b = 84000
          6          4       16800
          
       2.  
          
    3. B.P = sh. 77,000
       Maize
       S.P = 1600 × 110
                     100
             = sh. 1760
       Beans
       S.P = 1800 × 112.5
                      100
       S.P = (20 × 1760) + (25 × 2025)
            = sh. 85, 825
       Profit = sh. 85825 − 77,000
               = sh. 8,825
       % Profit = 8,825  × 100 %
                      77,000
                   = 0.115 × 100 %
                   = 11.5 %
20.  
    1. A = P (1 + ^r/₁₀₀)ⁿ
       = 1,240,000 (1 + ¹²/₁₀₀)⁹
       = 1,240,000 × 2.773
       = sh. 3,438,618
    2.  
       1. A = P (1 + ^r/₁₀₀)ⁿ
          2,741,245 = 1,240,000 (1 + ¹²/₁₀₀)ⁿ
             _{2.211                  1} 
          2,741,245 = 1,240,000
          1,240,00      1,240,000
          2.211 = (1.12)ⁿ
          log 2.211 = log 1.12 ⁿ
          
          log 2.211 = n log 1.12
           log 1.12        log 1.12
          = 0.3445 = n
             0.0492
          n= 7 years
       2. 2,917,231 = 1,2400,000 (1 + ^r/₁₀₀)⁷
           2,917,231 = 1,2400,000(1 + ^r/₁₀₀)⁷
          1,2400,000   1,2400,000
          2.3526 = (1 + ^r/₁₀₀)^{7
          7}√(2.3526) = 1 + ^r/₁₀₀
          1.13 − 1 = ^r/₁₀₀
          100 × 0.13 = ^r/₁₀₀ × 100
          r = 13 % p.a
21.  
    1.  
       1. T.I = B.S + T.A
              = 30,500 + 6000 + 4000 + 3000
                                       20
             = K£ 2175
       2. Gross tax
          325 × 2 = sh. 650
          325 × 3 = sh. 975
          325 × 4 = sh. 1300
          325 × 5 = sh. 1625
          325 × 6= sh. 1950
          550 × 7 = sh. 3850
          
          Gross tax = Ksh. 10,350
       3. net tax = Gross tax − relief
          = 10350 − 1056
          = Ksh. 9294
    2. Total dedcutions = 9294 + 150 + (200 × 2) + 2500
                               = Shs. 12,344
       Net Income = Sh. 43500 − 12,344
                        = Shs. 31,156
22.  
    1. P ∝ QR²
       P = kQR²
       18 = k × 9 × (15)²
       18 = 225 × 9 × k
         18   = 2025k
       2025    2025
       k = ²/₂₂₅
       ∴ P = ²/₂₂₅ QR²
       32 = ²/₂₂₅ × 81 × R²
       225 × 32 = 162R² × 225
           162         225       162
       44⁴/₉ = R²
       R = √44⁴/₉
          = 6²/₃
    2. A ∝  ^B/_√C
       A = k^B/_√C
       A = k × 0.9B
             √(1.21C)
       A = 0.9kB
             1.1√C
          = 0.818kB
                     √C
       B = 100%
          = 90%
       = 90 × 13 = 0.9B
             100 
       C = 100%
          = 121%
       121 × C = 1.21C
           100
       Δ in A: 0.818kB − kB
                         √C    √C
       = k  B(0.818 − 1)
            √C
       % Δ in A =  k ^B/_√C(0.818 − 1) × 100 %
                                     k^B/_√C
                    = − 0.1818 × 100%
       A decreases by 18.18%
23.  
    1.  
       1. S₈ = ⁿ/₂ (2a + (n−1)d)
          240 = ⁸/₂ ((2×2) + (8 −1)d)
          240 = 4 (4+7d)
          240 = 16 + 28d
          28d = 224 
          28       28 
          d = 8
       2. 2 × 1560 = ⁿ/₂ ((2×2) + (n − 1)8) × 2
          3120 = n (4+8n − 8)
          3120 = 4n + 8n² − 8n
             4       4      4        4
          780 = n + 2n² − 2n
          780 = 2n² − n
          2n² − n − 780 = 0
          n = −(−1) ± √(1+ 4×2×780)
                                  4
          = ⁸⁰/₂
          n = 40 times
    2.  
       1. a+2d, a+4d, a+2d ....G.P
          a+4d = a+7d
          a+2d    a+4d
          a² + 8ad + 16d² = a² + 9ad +14d²
          16d² − 14d² = 9ad − 8ad
          2d² = ad
            d       d
          a = 2d
          but d=3
          ∴ a = 6 (first term A.P)
       2. C.R = ¹⁸/₁₂ = ³/₂
          S_n = a (rⁿ − 1
                      r − 1
          S₉ = 12(1.5⁹ − 1)
                      1.5 − 1
          = 898.6
24.  
    1.  
       

       x	−4	−3	−2	−1	0	1	2
       2x2	32	18	8	1	0	2	8
       4x	−8	−12	−8	−4	0	4	8
       −3	−3	−3	−3	−3	−3	−3	−3
       y	21	3	−3	−6	−3	3	13

    2.  
       
    3.  
       1.   y = 2x² + 4x −3
          −0 = 2x² + x −5
          y = 3x + 2
          

          x	0	1
          y	2	5

          x = −2 or 1.4 ±0.1
       2.   y = 2x² + 4x −3
          −0 = 2x² + 3x −2
             y = x  − 1
          

          x	0	3
          y	−1	2

          x = 0.4 or −2 ± 0.1
       3. x = 0.6 or -2.6 ± 0.1

Please download this document as PDF to read all it's contents.

Why PDF Download?

• You will have the content in your phone/computer to read anytime.
• Study when offline.(No internet/data bundles needed.)
• Easily print the notes to hard copy.

Either

Click here to download the pdf version of "Mathematics Paper 2 Form 3 Questions and Answers - End Term 2 Exams 2021", and read the full contents of this page

OR

CLICK HERE to get "Mathematics Paper 2 Form 3 Questions and Answers - End Term 2 Exams 2021" on Whatsapp

OR