INSTRUCTIONS TO CANDIDATES
- This paper consist of two section A and B.
- Answer all questions in section A and B.
- All working must be clearly shown.
- Non- Programmable silent electronic calculators and KNEC mathematical tables may be used
SECTION A 25MARKS
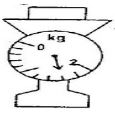
- The block of wood on the balance in the figure below is a cube of side 20cm Determine its density in kgm−3 (3mks)
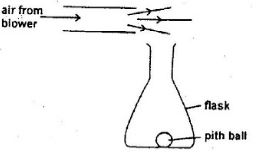
- The diagram below shows a pith ball in a flask. When a jet of air is blown over the mouth of the flask, the pith ball is found to rise from the bottom. Explain this observation (2mks)
- It is observed that a smelly gas released at the back of the laboratory spreads faster on a hot day than on a cold day. Explain (1mk)
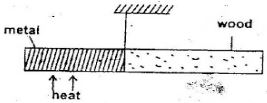
- The diagram below shows a rod made of wood on one end and metal on the other end suspended freely with a piece of thread so that it is in equilibrium
The side made of the metal is now heated with a Bunsen flame. State with reason the side to which the rod is likely to fit (2mks) - When a piece of metal is place in water it sinks. But when the same piece of metal is placed on a block of wood it floats explain the observation (2mks)
- A bullet traveling at a speed of 100ms−1 strikes a wall and penetrates 2cm. How long does the bullet take to stop after striking the wall? (3mks)
- A balloon of volume 1.5cm3 containing helium gas at a pressure of 3.0 x 106pa is released from the ground when the temperature is 20°C. What will be the pressure when it reaches a point where the volume becomes 3.0m and the temperature 5°C (3mks)
- Explain why mercury forms a convex meniscus and water a concave meniscus in a tube (2mks)
- A force of 3500N acts on a stationary body of mass 20kg for 0.02 seconds. Calculate the velocity attained by the body (2mks)
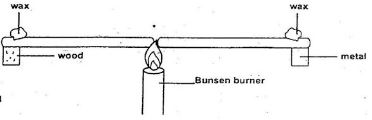
- The diagram below shows two identical iron rods, one is placed on a wooden block and the other on a metal block. The ends of the rods are heated as shown.
State with reason the piece of wax that melts first (2mks) - A stone is tied to a string and whirled in a horizontal circle at a constant speed. In which direction is the stone being accelerated at each point of its path? (1mk)
- A force of 2.0N compresses a spring by 1.0mm. Determine the energy stored in the spring
SECTION B 55MKS
-
- Define the term ‘velocity’. (1mk)
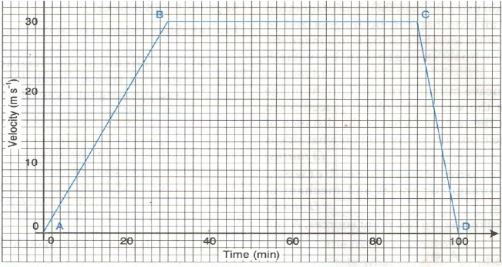
- The following figure shows velocity –time graph for the journey of a car in 100minutes.
- Determine the acceleration of the car between A and B and between C and D (4mks)
- Determine the distance covered by the car during the journey (3mks)
- Determine the average velocity of the car (2mks)
- A ball rolls off a platform of height 1.8m at a horizontal speed of 15 ms−1. How far off the edge of the platform does it land? (4mks)
- A car of mass 2000kg travelling at 5ms−1 collides with a minibus of mass 5000kg travelling in the opposite direction at 7ms−1. The vehicles stick and move together after collision. If the collision lasts for 0.1seconds;
- Determine the velocity of the system after collision of 3 decimal places. (3mks)
- Calculate the impulsive force on the minibus (3mks)
- Calculate the change in kinetic energy of the system (3mks)
- Explain the change in kinetic energy of the system (1mk)
-
- What is the difference between longitudinal and transverse waves? (2mks)
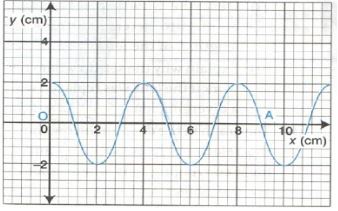
- The following figure shows a transverse wave travelling along the x-axis.
- Determine the wave length and the amplitude of the wave. (2mks)
- If the time taken by the wave to move from O to A is 0.04 seconds, determine the frequency and the speed of the wave (4mks)
- A person stands between two vertical cliffs 400m from the nearer cliff. The cliffs are x distance apart. Every time the person strikes the rock once, two echoes are heard, the first one after 2.5s and the second one 2.0 s later. Calculate
- the speed of the sound in air (3mks)
- the value of x (2mks)
-
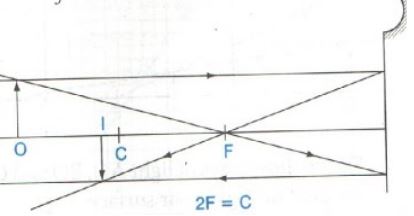
- The following figue shows an object, O, 3cm high placed in front of a concave mirror. C is the centre of curvature mirror. C is the centre of curvature of the mirror.
By constructing a ray diagram, determine the size and the position of the image formed. (3mks) - The table shows the object distance, u, and the corresponding image distance v, for an object placed in front of a concave mirror.
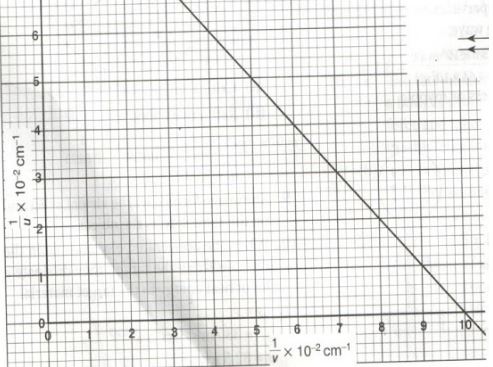
u (cm) 20 25 30 40 50 70 v(cm) 20 16.7 15 13.3 12.5 11.6 1/u (cm−1) 1/v (cm−1) - Complete the table by filling in the values of 1/u and 1/v (2mks)
- plot a graph of 1/u (y-axis) against 1/v (x-axis) (5mks)
- From the graph, determine the focal length of the mirror. (3mks)
- The following figue shows an object, O, 3cm high placed in front of a concave mirror. C is the centre of curvature mirror. C is the centre of curvature of the mirror.
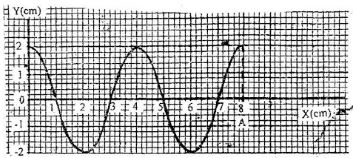
- The figure 6 shows a transverse wave travelling along the horizontal axis
determine- Wave length of the wave in metres (2mks)
- Amplitude of the wave (1mk)
- If the time take by the wave to move from O to A is 0.02seconds Determine frequency of the wave (3mks)

Marking Scheme
- The block of wood on the balance in the figure below is a cube of side 20cm Determine its density in kgm−3 (3mks)
Volume = 0.2m × 0.2m × 0.2m =0.008m3 √1
Mass = 1.6Kg √1
P= M = 1.6 =200kgm3 √1
V 0.008 - The diagram below shows a pith ball in a flask. When a jet of air is blown over the mouth of the flask, the pith ball is found to rise from the bottom. Explain this observation (2mks)
- The air velocity at the top of the flask is high hence low pressure.√1
- The high pressure inside the flask makes the ball to rise. √1
- It is observed that a smelly gas released at the back of the laboratory spreads faster on a hot day than on a cold day. Explain (1mk)
- Rate of diffusion increases with increase in temperature.√1
- The diagram below shows a rod made of wood on one end and metal on the other end suspended freely with a piece of thread so that it is in equilibrium
The side mad of the metal is now heated with a Bunsen flame. State with reason the side to which the rod is likely to fit (2mks)- Tilts to the left. √1
- The metal expands hence the centre of gravity (COG) shifts to the left. √1
- When a piece of metal is place in water it sinks. But when the same piece of metal is placed on a block of wood it floats explain the observation (2mks)
- The metal alone has a higher density than the liquid while the average density of the metal and the wood is less than that of the liquid.
- A bullet traveling at a speed of 100ms−1 strikes a wall and penetrates 2cm. How long does the bullet take to stop after striking the wall? (3mks)
V2 =u2 +2as
O2 =(100 × 100) +2 × 9 × 0.02m
a= −10000 =−2.5 × 105m/s √1
2 × 0.02
v= u + at √1
O = 100 + − 2.5 × 105 × t
t = 100 = 4 × 10−4s √1
2.5 × 105 - A balloon of volume 1.5cm3 containing helium gas at a pressure of 3.0 x 106pa is released from the ground when the temperature is 20°C. What will be the pressure when it reaches a point where the volume becomes 3.0m and the temperature 5°C (3mks)
V1 =1.5m3 V2 = 3.0m3
P1 = 3.0 × 106 Pa P2 = ?
T1 = 293K T2 = 278K√1
3.0 × 1.5 × 106 = 3.0 × P2 √1
293 278
P2 = 3.0 × 1.5 × 106 × 278
3.0
P2 = 4.17 × 108Pa √1 - Explain why mercury forms a convex meniscus and water a concave meniscus in a tube (2mks)
- The cohesive force between mercury particles exceeds the adhesive force between mercury and glass √1 while the cohesive force between water particles is lower than the adhesive force between water and glass particles.√1
- A force of 3500N acts on a stationary body of mass 20kg for 0.02 seconds. Calculate the velocity attained by the body (2mks)
Mv − Mu = Ft √1
20V − (20 × 0) = 3500 × 0.02
20V = 70
V = 70/20
=3.5m/s √1 - The diagram below shows two identical iron rods, one is placed on a wooden block and the other on a metal block. The ends of the rods are heated as shown.
State with reason the piece of wax that melts first (2mks)- The wax on the rod placed on wood melts first √1 wood does not conduct heat away as fast as metal hence the temperature of the rod on wood rises faster. √1
- A stone is tied to a string and whirled in a horizontal circle at a constant speed. In which direction is the stone being accelerated at each point of its path? (1mk)
- Towards the centre of the circular path. √1
- A force of 2.0N compresses a spring by 1.0mm. Determine the energy stored in the spring
E = ½FX
= ½ × 2 × 1.0
1000
=0.001J √1
SECTION B 55MKS
-
- Define the term ‘velocity’. (1mk)
- Velocity is the rate of change of motion in a specified direction. √1
- The following figure shows velocity –time graph for the journey of a car in 100minutes.
- Determine the acceleration of the car between A and B and between C and D (4mks)
a = slope of graph
= 30m s−1 √1
30 x 60s
= 0.016m s−2 √1
between C and D
a=−30m s−1 √1
10 x 60s
= 0.05m s−2 √1 - Determine the distance covered by the car during the journey (3mks)
Distance = area under graph
=30ms−1 x ( 100 + 60) x 60s
2
= 144 000m. - Determine the average velocity of the car (2mks)
Vav = total distance
total time
= 144 000m √1
100 x 60s
= 24ms−1 √1
- Determine the acceleration of the car between A and B and between C and D (4mks)
- A ball rolls off a platform of height 1.8m at a horizontal speed of 15 ms−1. How far off the edge of the platform does it land? (4mks)
S = ½ gt2 √1
1.8m = ½ x 10m s−1 x t2
t2 = 0.36s2
t = 0.6s √1
s = vt √1
= 15m s−1 x 0.6s =9m √1
- Define the term ‘velocity’. (1mk)
- A car of mass 2000kg travelling at 5ms−1 collides with a minibus of mass 5000kg travelling in the opposite direction at 7ms−1. The vehicles stick and move together after collision. If the collision lasts for 0.1seconds;
- Determine the velocity of the system after collision of 3 decimal places. (3mks)
Momentum before collision = momentum after collision
M1U1 +M2 (−U2) = (M1 + M2) V
(2000 x 5)2 +5000 x (−7) = 7000V √1
V = −25000
7000
= −3.571 ms−1 √1 - Calculate the impulsive force on the minibus (3mks)
Ft = M(V−U)
f = m(V−U) √1
t
F = 5000 ( −3.571 − (−7) √1
0.1
F = 171,450 N √1 - Calculate the change in kinetic energy of the system (3mks)
initial K.E = ½ M1U12 + ½ M2 (−U2)2
= ½ x 2000 X 52 + ½ x 5000 x (−7)2
= 25,000 + 122, 500
= 147,500J √1
final K.E + ½ (M1 +M2) V2
= ½ (2000 + 5000) (−3.571)2
= 44,632 J √1
Change in K.E = K.E lost − final K.E − Initial K.E
= (44,632 − 147,500) J
= −102,868J √1 - Explain the change in kinetic energy of the system (1mk)
- The change /lost K.E is converted into heat, sound, light and spent in deformation
- Determine the velocity of the system after collision of 3 decimal places. (3mks)
-
- What is the difference between longitudinal and transverse waves? (2mks)
- Particles of the transmitting medium vibrate in the direction of the wave for a longitudinal wave, but at right angles for a transverse wave.
- The following figure shows a transverse wave travelling along the x-axis.
- Determine the wave length and the amplitude of the wave. (2mks)
- Wavelength = 4cm √1
- Amplitude = 2cm √1
- If the time taken by the wave to move from O to A is 0.04 seconds, determine the frequency and the speed of the wave (4mks)
O to A = 9cm containing 2 ¼ waves
Time = 0.045 √1
2 ¼
f = 1/T
= 1
0.04s/2 ¼
f = 56.25Hz. √1
v = f^ √1
= 56.25 x 0.04
=2.25ms−1 √1
- Determine the wave length and the amplitude of the wave. (2mks)
- A person stands between two vertical cliffs 400m from the nearer cliff. The cliffs are x distance apart. Every time the person strikes the rock once, two echoes are heard, the first one after 2.5s and the second one 2.0 s later. Calculate
- the speed of the sound in air (3mks)
s = 2d
t
= 2 x 400
2.5
= 320ms−1 - the value of x (2mks)
2(x − 400) = (2.5 +2)s √1
x = 1120m √1
- the speed of the sound in air (3mks)
- What is the difference between longitudinal and transverse waves? (2mks)
-
- The following figue shows an object, O, 3cm high placed in front of a concave mirror. C is the centre of curvature mirror. C is the centre of curvature of the mirror.
By constructing a ray diagram, determine the size and the position of the image formed. (3mks)
image − real and inverted
f = 2.4 ± 0.1cm.
- 2rays with arrows √2
- inverted image √1
- The table shows the object distance, u, and the corresponding image distance v, for an object placed in front of a concave mirror.
u (cm) 20 25 30 40 50 70 v(cm) 20 16.7 15 13.3 12.5 11.6 1/u (cm−1) 0.05 0.04 0.033 0.025 0.020 0.014 1/v (cm−1) 0.05 0.06 0.067 0.075 0.08 0.086 - Complete the table by filling in the values of 1/u and 1/v (2mks)
- plot a graph of 1/u (y-axis) against 1/v (x-axis) (5mks)
A-√1
S-√1
P-√2
L-√1 - From the graph, determine the focal length of the mirror. (3mks)
1/f = 1/u + 1/v intercept = 1/f √1
0.1 = 1/f √1
f = 10cm √1
- The following figue shows an object, O, 3cm high placed in front of a concave mirror. C is the centre of curvature mirror. C is the centre of curvature of the mirror.
- The figure 6 shows a transverse wave travelling along the horizontal axis
determine- Wave length of the wave in metres (2mks)
0.04M √1 correct reading
√1 correct units - Amplitude of the wave (1mk)
2cm √1 - If the time take by the wave to move from O to A is 0.02seconds Determine frequency of the wave (3mks)
F = 1/T √1
1 √1
0.01
=100HZ √1
- Wave length of the wave in metres (2mks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Physics Paper 2 Questions and Answers - Form 3 Mid Term 1 Exams 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students