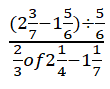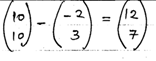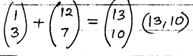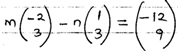Instructions
- Answer all the questions in section I and ONLY Five in section II.
- Show all the calculations in the spaces provided
- KNEC mathematical tables and non-programmable calculators may be used.
SECTION I
- Evaluate without using a calculator. [1 Mark]
- The equation of a straight line L1 is 3y+4x=12
- Find the gradient of L1 [1 Mark]
- The equation of another line L2 which is perpendicular to L1 and passes through (1,2) [2 Marks]
- Evaluate using mathematical tables only expressing your answer to 4 significant figures. [3 Marks]
3 + (0.7918)2
0.2311 - Given that:
sin (3x−35)= cos (x+20). Find x [2 Marks] - The size of an interior angle of a regular polygon is (3x)° while the exterior angle is (x−20)°. Find the number sides of the polygon [3 Marks]
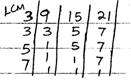
- Three bells ring at intervals of 9 minutes, 15 minutes and 21 minutes. The bells will next ring together at 11.00pm. Find the time the bells had last rung together. [3 Marks]
- Find all the integral values of x which satisfy the following inequalities [3 Marks]
2(2−x)<4x−9<x+11 - At a party, every two people shared a plate of Ugali between them. Every 3 people shared a plate of soup and every 4 people shared a plate of meat. If 65 plates were used in total. How many people were there? [3 Marks]
- Find the value of x which satisfies the equation; [3 Marks]
- Mary and John live 140km apart. Mary starts from her home at 7.00am and drives towards John’s home at 80km/hr. John starts at 7.30am and drives towards Mary’s home at 100km/hr. at what tome did they meet? [3 Marks]
- Two points P and Q have coordinates (−2, 3) and (1, 3) respectively. A translation maps point P to P1 (10,10).
- Find the translation vector [1 Mark]
- Find the coordinates of Q the image of Q under the translation. [1 Mark]
- Find the values of M and N if;
mP − nQ =[3 Marks]
- A Kenyan company received $100,000 US dollars. The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows;
Buying. Selling
1 US Dollar ($) 77.23 78.11
1 Sterling Pound (£) 121.04 122.93- Calculate the amount of money, in Kenya shillings the company received[2 Marks]
- The company exchanged the Kenya-shilling calculated in (a) above into sterling pounds to buy a car from Britain. Calculate the cost of the car to the nearest sterling pound. [2 Marks]
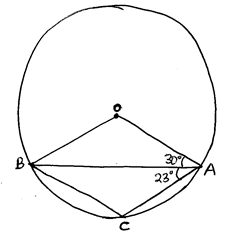
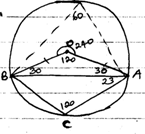
- In the figure below, O is the centre of the circle. Angle OAB=30° and angle BAC = 23°. Find angle ABC. [3 Marks]
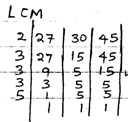
- A number n is such that when it is divided by 27, 30 or 45, the remainder is always 3. Find the smallest value of n. [2 Marks]
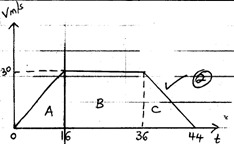
- A particle accelerates uniformly from rest and attains a maximum velocity of 30m/s. after 16 seconds. It travels at this constant velocity for 20 seconds before decelerating to rest after another 8 seconds.
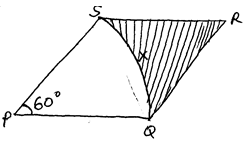
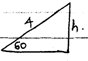
Calculate the total distance travelled by the particle. [4 Marks] - The figure below shows a rhombus PQRS with PQ=9cm and <SPQ=60°,S×Q is a circular arc center P.
Calculate the area of the shaded region correct to 2 decimal places. [3 Marks]
SECTION II
Answer any 5 Questions in this Section. (50 Marks)
- A salesman received a basic salary of sh. 50,000 a year together with a commission of 6% on the value of goods sold and a car allowance of sh. 2.50 per km.
- Find the total amount he received in a year in which he sells goods worth sh. 625,000 and travels 10,000km. [4 Marks]
- The next year he travels 12,000km and receives a total of sh. 134,000.
- Calculate the value of goods sold. [4 Marks]
- Calculate the percentage increases in the value goods sold. [2 Marks]
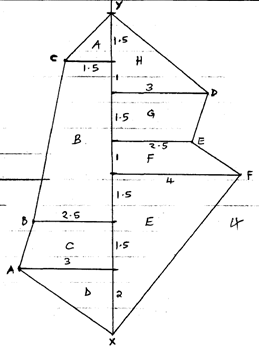
- The following measurements were recorded in a field book at a farm using XY=400m as the baseline.
C60
B100
A120Y
340
300
240
200
140
80
X120D
100E
160E- Using the scale of 1:4000 (1cm represents 40m) draw accurately the map of the farm. [4 Marks]
- Determine the actual area of the farm in hectares. [4 Marks]
- If the farm is on sale at Ksh. 80,000 per hectare, how much does the farm cost?
[2 Marks]
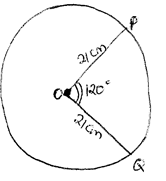
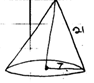
- The minor arc PQ of a circle radius 21cm subtends an angle of 120° at the centre of the circle as shown below.
- Find the area of the minor sector POQ [2 Marks]
- Find the perimeter of the minor sector POQ [3 Marks]
- The minor sector POQ is folded to form a right circular cone.
Calculate:- The radius of the cone. [3 Marks]
- The height of the cone. [2 Marks]
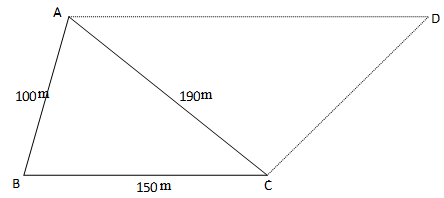
- A triangular piece of land ABC has sides AB=100m, BC=150m and AC=190m.
- Calculate the area of the triangular piece of land ABC [2 Marks]
- Calculate the value of angle ACB. [3 Marks]
- A new piece of land ABCD is a trapezium with AD//BC whose area is three times that of triangle ABC, calculate the perimeter of ABCD. [5 Marks]
- Three business partners, Bela, Joan and Trinity contributed Kshs. 112, 000, Kshs. 128, 000 and Kshs. 210, 000 respectively to start a business. They agreed to share their profits as follows:
30% to be shared equally
30% to be shared in the ratio of their contributions
40% to be retained for the running of the business.- If at the end of the year, the business realised a profit of Kshs. 1. 35million
Calculate: - The amount of money retained for running the business at the end of the year.
[1 Mark] - The difference between the amounts received by Trinity and Bela. [6 Marks]
- Express Joan’s share as percentage of the total amount of money shared between the three partners. [3 Marks]
- If at the end of the year, the business realised a profit of Kshs. 1. 35million
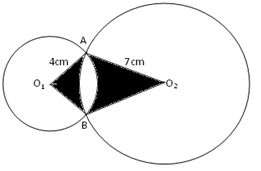
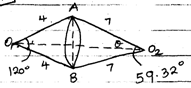
- In the figure below, O1 and O2 are the centres of the circles whose radii are 4 cm and 7 cm respectively. The circles intersect at A and B and angle AO1O2 = 60˚
Find by calculation; take π = 3.142- The angle AO2O1 [1 Mark]
- The area of the quadrilateral AO1BO2 [4 Marks]
- The shaded area [5 Marks]
- Members of a certain group decided to raise sh. 225,000 to buy a plot of land, with each contributing the same amount. Before the due date for collection of the contribution, ten of the members withdrew from the project.
- Letting n represent the original membership of the group, show that the increase in contribution per member was 2250000 [4 Marks]
n(n-10) - If the increase in contribution per person was sh. 1125, what was the original number of members in the group? [4 Marks]
- Calculate the percentage increase in the contribution per person caused by the withdrawal of the members. [2 Marks]
- Letting n represent the original membership of the group, show that the increase in contribution per member was 2250000 [4 Marks]
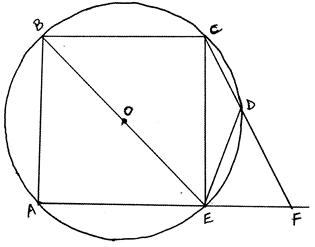
- In the figure below, O is the center of the circle. <AEB=50°, <EBC=80° and <ECD=30°
Giving reasons calculate- <CDE [2 Marks]
- <DFE [2 Marks]
- Obtuse <COE [2 Marks]
- <ADE [2 Marks]
- <CAE [2 Marks]

MARKING SCHEME
- 17/7 − 11/6 = 102 − 77 = 25/42
42
525 × 61 = 5
742 51 7
2/3 of 9/4 = 3/2 − 8/7 = 21 −16 = 5/14
14
5/7 × 14/5 = 2 -
- 3y/3 = −4/3x + 12/3
y = −4/3x + 4
G = −4/3 - −4/3x = −1
x = ¾
y − 2 = ¾
x − 1
4y − 8 = 3x− 3
4y = 3x + 5
y = ¾x + 5/4
- 3y/3 = −4/3x + 12/3
- 3 × 1
0.2311
2.311 × 10−1
0.4327 × 101
= 4.327
× 3
12.981
(7.918 × 10−1)2
62.70×10−2 = 0.6270
12.981 + 0.6270
= 13.608 - 3x − 35 + x + 20 = 90
47 − 15 = 9
4x = 105
x = 26¼° - 3x + x − 20 = 180
4x = 200
x = 50°
exterior = 50 − 20 = 30°
n = 360 = 360 = 12 sides
ext 30 -
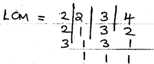
3 × 3 × 5 × 7 = 315 minutes
= 5hrs 15mins
11:00
−5:15
5:45
=5:45pm - 4 − 2x < 4x − 9
13/6 < 6x/6
21/6 < x
4x − 9 < x +11
3x/3 < 20/3
x < 62/3
21/6 < x < 62/3
integral values; ( 3, 4, 5, 6) -
2 x 2 x 3 = 12
12/2 = 6 plates of Ugali
12/3 = 4 plates of soup
12/4 = 3 Plates of Meat
12 people = 13 plates
65 plates
12 x 65 = 60 people
13 -
4x2 = 12x − 9
4x2 −12x + 9 =0
4x2 − 6x − 6x + 9 = 0
2x(2x−3) −3(2x−3) =0
(2x − 3)(2x−3) = 0
x= 1.5
½ × 80 = 40km
Relative speed = 80 + 100 = 180km/hr
T= D/S = 100/180 = 33mins
7.30
+ 33
8.03 am.-
-
-
3(−2m−n=−12)
2(3m − 3n = 9) -−
−6m − 3n = − 36
+ 6m − 6 = 18
− 9n = −18
n = 2
−2m =−10 m = 5
- 1 US Dollor Buying 77.23
- 100,000 = 7,723000
- 7,723,000 = 62824 pounds
122.93
120 +23 = 143°
180 − 143 = 37°
<ABC = 37°-
270 + 3 =273 -
D = Area under velocity time graph
A = ½ ×16 × 30 = 240m
B = 20 × 30 = 600m
C = ½ × 8 × 30 =120m
Total distance = 960m - Area of rhombus
½ x 9 x 9 Sin 60 × 2
= 81 sin 60
=70.148 cm
Area of sector
3.142 × 9 × 9 × 60 = 42.417
360
70.148 − 42.417
= 27.731 cm2 -
- 6/100 × 625000
= 37500/=
Shs 2.50 = 1km
10,000
= 25,000
Total = 50,000 + 37500 + 25000
= Shs 112,500 -
- 134000 − 50,000 = 84,000
12000 x 2.5 = 30,000
Commission = 84000 − 30,000
= 54000
100 × 6 x = 54000 × 100
6 100 6
Value of goods = 900,000/= - 900,000
−625,000
275,000
275000 × 100 = 44%
625000
- 134000 − 50,000 = 84,000
- 6/100 × 625000
-
- A = ½ × 1.5 × 1.5 = 1.125cm2
B = ½ × 4 × 5 = 10cm2
C = ½ × 5.5 × 1.5 = 4.125cm2
D = ½ × 2 × 3 = 3cm2
E = ½ × 4 × 5 = 10cm2
F = ½ × 6.5 × 1 = 3.25cm2
G = ½ × 5.5 × 1.5 = 4.125cm2
H = ½ × 2.5 × 3 =3.75cm2
39.375cm2
1cm rep 40m
1cm2 =1600m2
39.375
39.375 × 1600 = 63000m2
10000
= 6.3ha - 6.3 × 80000 = Shs 504,000
-
- πr2 θ/360
A = 22/7 × 21 × 21 × 120/360
= 462cm2 - πDθ/360
22/7 × 12 × 120/360 = 44cm
44+42=86cm -
- 44cm = 22/7D
D = 7/22 × 44 =14/2 = 7cm -
√(212 − 72)
√392
= 19.8cm
- 44cm = 22/7D
- πr2 θ/360
- Hero's formula
- S = ½(100+190+150)
A = √(280(220−150)(220−100)220−190))
A = √(55.44 × 106)
= 7. 446 × 103 = 7446m2 - <ACB
Cos C =
Cos C = 48600 = 0.8526
57000
C = Cos−1 0.8526
<ACB = 31.5° - 7446×3
ABCD = 22338m2
Area of ACD
22338 − 7446
= 14892m2
7446 = ½ × 160 × h
7446 = 75h
75 75
h =99.28m
ABCD
= ½ × (150+AD) × 99.28 = 22338
150 + AD = 450
AD = 300m
<CAD = 31.5°
(CD)2 = 1902 + 3002 −2 × 190 × 300 cos 31.5
(CD)2 = 36100 + 90000 − 97201
(CD)2 = 28899
CD = 170m
Perimeter = 100+150+170+300
=720m
- S = ½(100+190+150)
-
- 40/100 × 1350000
= 540,000 - 30/100 × 1350000
=405000
405000 = 135000each
3
B : J : T
112:128:210
56 : 64 :105
Bela = 56/225 × 405000 = 100,800
Total(Bela) = 135000+100800
=235,800
Trinity = 105/225 × 405000 = 189000
Total = 189000 + 135000
=324,000 - Difference = 324000 − 235800
= Shs 88,200 - (64/225 × 405000) + 135000
= 250,200
250,200 × 100
810,000
= 308/9%
- 40/100 × 1350000
-
-
sin 60° = h/4 h= 3.464
Sin θ = 3.464
7
θ = Sin−1 = 29.66° - ½ × 4 × 4 sin 120 = 6.93cm2
½ × 7 × sin 59.32 = 21.072
=28cm2 - Unshaded area
sector 1
πr2 θ/360
3.142 × 4 × 4 × 120/360 = 16.76cm2
∆O1AB = 6.93
16.76 − 6.93 = 9.83cm2
Sector 2
3.142 × 7 × 7 × 59.32 = 25.37cm2
360
25.37 − 21.07 = 4.3cm2
sum
9.83+4.3 = 14.13cm2
Shaded area
28 − 14.13 = 13.87cm2
-
-
- Original contribution = 225000
n
After 10 withdrew = 225000
n−10
225000 − 225000
n−10 n
n(n−10)
225000n −225000n+2250000
n(n−10)
= 2250000
n(n−10) - 2250000 = 1125
n(n−10)
n(n−10) = 2000
n2−10n−2000=0
n2 − 50n + 40n − 2000 =0
n(n−50) + 40(n−50)=0
(n+40)(n−50) = 0
n = 50 members - 225000 = 4500
50
225000 = 5625
40
1125 × 100
4500
=25%
- Original contribution = 225000
-
- <CDE = 100°
=Opposite angles in a cyclic quadrilateral BCDE - <DFE = 30°
= Angle sum of triangle DEF add up to 180° - <COE = 160°
= Radius subtends equal angles at the circumference. - <ADE = 40°
=Angle subtended by chord AE at the circumference. - <CAE = 80°
= Angle subtended by chord CE at the circumference.
- <CDE = 100°
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Form 3 Mid Term 2 Exams 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students