INSTRUCTION TO STUDENTS:
- Write your name, admission number and class in the spaces provided above.
- Write the date of examination in spaces provided.
- This paper consists of two Sections; Section I and Section II.
- Answer ALL the questions in Section I and only five questions from Section II.
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- KNEC Mathematical tables may be used, except where stated otherwise.
- Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.
- Candidates should answer the questions in English.

QUESTIONS
Ensure that all the pages are printed and no question(s) are missing
SECTION 1 (50 marks)
- Without using a calculator evaluate,
-2(5+3) - 9÷3+5 (3 marks)
-3 × -5+-2 × 4 - Three bells ring at intervals of 9 minutes, 15 minutes and 21 minutes. The bells will next ring together at 11.00 pm. Find the time the bells had last rang together. (3 marks)
- A construction company employs technicians and artisans. On a certain day 3 technicians and 2 artisans were hired and paid a total of Kshs 9000. On another day the firm hired 4 technicians and 1 artisan and paid a total of Kshs 9500. Calculate the cost of hiring 2 technicians and 5 artisans in a day. (3 Marks)
- A Kenyan company received US Dollars 100,000.The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows:
Buying (in Kenya shillings) Selling(in Kenya shillings)
1 US Dollar 77.24 77.44
1 Sterling Pound 121.93 122.27- Calculate the amount of money, in Kenya shillings, the company received. (2 marks)
- The company exchanged the Kenya shillings calculated in (a) above, into sterling pounds to buy a car from Britain. Calculate the cost of the car to the nearest sterling pound. (2 marks)
- The size of an interior angle of a regular polygon is 3xº while its exterior angle is ( x- 20)º. Find the number of sides of the polygon . (3 marks)
- Simplify
(3marks)
- In fourteen years time, a mother will be twice as old as her son. Four years ago, the sum of their ages was 30 years. Find how old the the mother was, when the son was born. (4mks)
- Given that Sin (x+ 60º) = Cos (2x)º, find Tan (x+60)º (3 marks)
- A cylindrical solid whose radius and height are equal has a surface area of 154 cm2.Calculate its diameter, correct to 2 decimal places.(Take π =3.142). (3marks)
- A square brass plate is 2 mm thick and has a mass of 1.05 kg. The density of the brass is 8.4 g/cm3. Calculate the length of the plate in centimeters. (3 marks)
- Simplify a + b (3 Marks)
2(a+b) 2(a- b) - Chelimo’s clock loses 15 seconds every hour. She sets the correct time on the clock at 0700h on a Monday. Determine the time shown on the clock when the correct time was 1900h on Wednesday the same week. (3 mks)
- The volume of a cube is 1728cm3. Calculate, correct to 2 decimal places, the length of the diagonal of a face of the cube. (3 Marks)
- Given the inequalities x – 5 ≤ 3 x – 8 < 2 x – 3.
- Solve the inequalities; (2 marks)
- Represent the solution on a number line. (1 mk)
- Given that OA = 2i + 3j and OB = 3i - 2j. Find the magnitude of AB to one decimal place. (3 marks)
- The production of milk, in litres, of 14 cows on a certain day was recorded as follows
22, 26, 15, 19, 20, 16, 27, 15, 19, 22, 21, 20, 22 and 28.- The mode; (1 mk)
- The median. (2 marks)
SECTION II(50 marks)
CHOOSE ANY FIVE QUESTIONS IN THIS SECTION
- A farmer had 540 bags of maize each having a mass of 112kg. After drying the maize, the mass decreased in the ratio 15:16.
- Calculate the total mass lost after the maize was dried. (3 marks)
- A trader bought and repacked the dried maize in 90 kg bags. He transported the maize in a lorry which could carry a maximum of 120 bags per trip.
- Determine the number of trips the lorry made. (3 marks)
- The buying price of a 90 kg bag of maize was Ksh 1,500. The trader paid Ksh 2,500 per trip to the market. He sold the maize and made a profit of 26 %. Calculate the selling price of each bag of the maize. (4 marks)
- The floor of a room is in the shape of a rectangle 10.5m long by 6m wide. Square tiles of length 30cm are to be fitted on to the floor.
- Calculate the number of tiles needed for the floor. (2mks)
- A dealer wishes to buy enough tiles for fifteen such rooms. The tiles are packed in cartons each containing 20 tiles. The cost of each carton is kshs. 800. Calculate:
- The total cost of the tiles (3mks)
- If in addition the dealer spends kshs. 2,000 and Kshs. 600 on transport and subsistence respectively, at what price should he sell each carton in order to make a profit of 12.5% (to the nearest Kshs) (5mks)
- The boundaries PQ,QR,RS and SP of a ranch are straight lines such that: Q is 16 km ona bearing of 040º from P;R is directly south of Q and east of P and S is 12 km on a bearing of 120º from R.
- Using a scale of 1 cm to represent 2 km. Show the above information in a scale drawing. ( 3mks)
- From the scale drawing determines:
- The distance in kilometers of P from S. (2Mrks)
- The bearing of P from S.(2Mrks)
- Calculate the area of a ranch PQRS in square kilometers. (3Mrks)
- A line L passes through (-2, 3) and (-1, 6) and is perpendicular to a line P at (-1, 6).
- Find the equation of L (2marks)
- Find the equation of P in the form ax + by = c,where a, b and c are constants. (2marks)
- Given that another line Q is parallel to L and passes through point (1, 2) find the x and y intercepts of Q (3marks)
- Find the point of the intersection of lines P and Q (3marks)
-
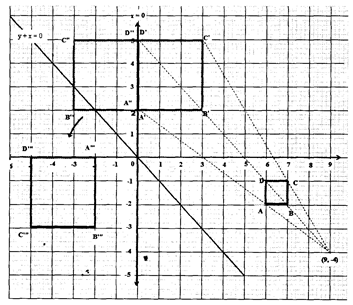
- On the grid provided, draw the square whose verticals are A (6, -2), B (7, -2), C (7, -1) and D (6, -1). (1 mk)

- On the same grid, draw:
- AʹBʹCʹDʹ, the image of ABCD, under an enlargement scale factor 3, centre (9, -4); (3 marks)
- AʹʹBʹʹCʹʹDʹʹ, the image of AʹBʹCʹDʹ, under a reflection in the line x = 0; (2 marks)
- AʹʹʹBʹʹʹCʹʹʹDʹʹʹ, the the image of AʹʹBʹʹCʹʹDʹʹ under a rotation of + 900 about (0,0) (2 marks)
- Describe a single transformation that maps AʹBʹCʹDʹ onto AʹʹʹBʹʹʹCʹʹʹDʹʹʹ (2 marks)
- On the grid provided, draw the square whose verticals are A (6, -2), B (7, -2), C (7, -1) and D (6, -1). (1 mk)
- The figure below represents a cone of height 12 cm and base radius of 9 cm from which a similar smaller cone is removed, leaving a conical hole of height 4 cm.
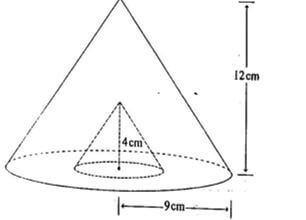
- Calculate:
- The base radius of the conical hole; (2 mks)
- The volume, in terms of π, of the smaller cone that was removed. (2 mks)
- Determine the slant height of the original cone. (1 mk)
- Calculate, in terms ofπ, the surface area of the remaining solid after the smaller cone is removed. (5mrk)
- Calculate:
- The figure below represents a speed time graph for a cheetah which covered 825min 40 seconds.
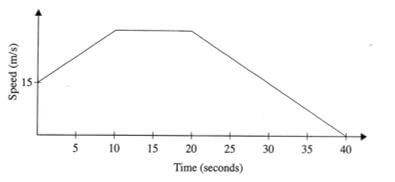
- State the speed of the cheetah when recording of its motion started (1 mark)
- Calculate the maximum speed attained by the cheetah (3marks)
- Calculate the acceleration of the cheetah in:
- The first 10 seconds (2marks)
- The last 20 seconds (1mark)
- Calculate the average speed of the cheetah in first 20 seconds (3marks)
- A saleswoman is paid a commission of 2% on goods sold worth over Ksh 100,000. She is also paid a monthly salary of Ksh 12,000.In a certain month, she sold 360 handbags at Ksh 500 each.
- Calculate the saleswoman’s earnings that month. (3 marks)
- The following month, the saleswoman’s monthly salary was increased by 10%.Her total earnings that month were Ksh 17,600.
Calculate:- The total amount of money received from the sales of handbags that month. ( 5marks)
- The number of handbags sold that month. (2 marks)

MARKING SCHEME
- -2(5 + 3) - 9 ÷3 + 5 = - 14√√
-3 x -5 + (-2) x 4 7
= -2 √ - LCM of 9, 15 and 21
32 x 5 x 7 = 315 minutes√
Last time ringing together
11.00 23.00
5.15 5.15
5.45 p.m.√ 1745hrs√ - let a technician be x and artisan be y
3x + 2y = 9000
4x + 1y = 9500
8x+2y = 19000
3x +2y = 9000
5x/5 = 10000/5 = 2000..........................√
Hiring a technician = 2000√
Hiring artisan
4(2000) + y = 9500
Y= 1500
2(2000) + 5(1500) = 11,500√ -
- sh 77.24 x 100,000√
= sh 7,724,00√ - Sh 77.24 x 100 000
= 63172√
122.27√
- sh 77.24 x 100,000√
- 3x + (x-20) = 180º
4x = 200º
X = 50º√
(x-20)n=360
30n=360√
n = 12 √ - 243 - 2/5 x 1252/3 = 3-2 x 52 √
9 - 3/2 3-3
= 27 × 25
9√
= 75 √ - let mother’s year be x and son’s be y now:
X+14=2(y+14) .................................(i)
X+14= 2y+ 28
x-2y = 14...........................................(ii) √
(x-4)+(y-4) =30
X+y=38 ............................................(iii) √
(iii)-(ii)
X+y=38
-x+2=-14
3y=24
Y=24 x=30√
At son’s birth: mother’s age
30-8=22 √ - Sin (x + 60º) = cos 2x
X + 60 + 2x = 90º
3x = 30√
x = 100
Tan (10 + 60)º = tan 70º√
2.748(4.S.F) from tables √ - 2πr2 + 2πrh = 154
r = h
2πr3 + 2πr2 = 154√
4πr2 = 154
r = √ 154
4 × 3.142√
= 3.500
diameter = 2r= 3.500 x 2
= 7.00 (s dp) √ - Volume of plate = 1.05 x 100√
8.4
= 125cm3
L2= 125 cm = 625 √
0.2
L = √625 = 25cm √ - a(a-b)(a+b)
(2(a+b)(a-b)
a2-ba+ba+b 2
2a+2b) (a-b)√
a2+ b2
2a2- 2ab+2ab-2b2 ) √
a2+ b2
2a2- 2b2
a2+ b2
2(a2- b2) √ - From 0700h Monday to 1900h Wednesday
= 24 x 2 + 12 h
=60h√
Time lost = 60 x 15 = 900 sec
=15 min√
Time shown on clock:
1900 h – 15 min = 1845 h√ 
∛1728 = 12√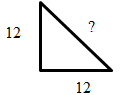
√122 + 122
=√288 =16.97 cm√-
- x-5≤3x - 8
-2x≤-3√
3x - 8 < 2x -3
x<5
∴ 1.5 ≤ x <5√ -
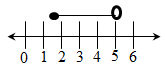
- x-5≤3x - 8
- (3/-2) - (2/3) √
= (1/-5)
Magnitude = √12+(-5)2 √
= √26 ≈ 5.1 √ -
- mode
=22√ - Median
15,15,16,19,19,20,20,21,22,22,22,26 ,27,28
Median = 20+21
2 √
= 20.5 √
- mode
-
- mass after decrease
112 x 15/16
= 105 kg√
Total decrease
(112-105) x 540√
=3780 kg√ -
- no. of 90kg bags
105 x 540
90 √
=630
Least number of trips
630
120√
= 5.25
6 trips√ - Expenses
Buying price = 1500 x 630 = 945000√
Transport = 1500 x 630 = 945000
Total 945000 + 15000√
Selling price per bag:
= 960000 x 1.26 = 1920√√
630
- no. of 90kg bags
- mass after decrease
-
- 10.5 x100x6x100=630,000cm3
Area of the tile = 30 x 30 = 900 cm2√
No of tiles = area of the floor
area of one tile
= 630000 =700 tiles√
900 -
- 1 carton = 20 tiles
? = 700 tiles
700 x 1 =35 cartons. √
20
1 carton = 800 sh.
35 Cartons = 35 x 800 = 28,000sh√
1
1 room =28,000 sh.
15 rooms = 28000 x 15 =420,000sh
1
= sh. 420,000√ - Transport = 2000
subsistence = 600
2000 + 600 = 2600sh√
Total cost = 420,000 +2600
=Ksh. 422,600√
12.5 x 422,600 = 52,825sh
100
Profit = 52,825sh
Cost price = 422,600sh
Selling price = 422,600sh + 52,825√
=475,425sh
35 cartons = 475,245
1 carton= 475425
1 carton = 475,425 x 1 13,584sh√√
35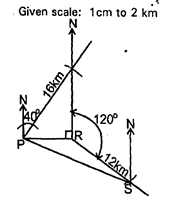
- 1 carton = 20 tiles
- 10.5 x100x6x100=630,000cm3
-
- a)
-
- Distance of P from s =10. 8 + 0.1cm
- < PSN = 74 + 10√
earing of P from S = 286 + 10
- area of PQR = ½ x 10.2 x 12.2
= 63.44km2
Area of PRS = ½ x 10.2 x 2 sin-600
= 30.6km2
Area of ranch PQRS
= 62.22 + 30.6
= 92.82km2
-
- Equation of L
Gradient = 6 - 3
-1- -2
=3
Equation =y - 6 =3
x+1
=y-3x=9√ - Equation of P√
=y - 6 =-1/3
x+1
= 3y + x =17√ - Equation of Q
= y - 2 =3
x - 1
= y=3x-1√
x intercept
When y = 0 ⇒ x = + 1/3
y intercept √
When x = 0 ⇒ y = -1√ - Intersection of lines P and Q
3y + x=17……(i)
y-3x= -1…….(ii)
3y+x=17√
3y-9x=-3
10x=20 ⇒x=2
Subset 3y+2=17⇒y=5
∴point of intersection (2,5) √
- Equation of L
-
-
-
- A'(0,2), B'(3,2), C'(3,5), D'(0,5)
- A''(0,2), B''(3,2), C''(-3,5), D''(0,5)
- A'''(-2,0), B'''(-2.-3), C'''(-5,-3), D'''(-5,0)
- Reflection in the line y + x = 0
-
-
-
- r/9 = 4/12
R = 9 x 4 = 3 cm
12 - Volume of material drilled out
= 1/3 π x 32 x 4 = 12π
- r/9 = 4/12
- Slant height of cone
=√92+ 122) = 15 cm - Surface area of solid after conical has been drilled
π x 9 x 9 x 15 + π x (92- 32) + π x 3 x 5
= π(135+72+15)
= 222π - [1/5 (15+30)×10+10×30]÷20
= (225+300)÷20
=26.25 m/s
-
-
- 15m/s
- Maximum speed
½ (15+h) × 10+½ (10+30)h=825
75+5h+20h=825
25h=750
h=30m/s -
- = 30-15
10
= 1.5m/s2 - =0 - 30= -1.5m/s2
20
- = 30-15
-
- total sales = sh 360 x 500
= sh.180,000√
Commission
= sh (180,000 – 100,000) x 2/3 √
= 13600√ -
- New salary
= sh.(12000 + 12000 x 10/100) √
= sh. 13200√
Commission paid
= Sh (17,600 -13,200)
= Sh.4400√
Commission is paid on sh.4400 x 100/2
= 220,000√
Total sales = sh.220,000 + 100,000 √
=320,000/=√ - No of handbags sold = 320,000/500 = 640 √
- New salary
- total sales = sh 360 x 500
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics P1 Questions and Answers - Form 3 Term 3 Opener Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

