Mathematics P2 Questions and Answers - Form 3 Term 3 Opener Exams 2022

INSTRUCTION TO STUDENTS:

• Write your name, admission number and class in the spaces provided above.
• Write the date of examination in spaces provided.
• This paper consists of two Sections; Section I and Section II.
• Answer ALL the questions in Section I and only five questions from Section II.
• All answers and working must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• KNEC Mathematical tables may be used, except where stated otherwise.
• Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.
• Candidates should answer the questions in English.

QUESTIONS

SECTION 1 (50 Marks)
Answer all the questions in the spaces provided.

1. Simplify completely (3mks)
   2x² + x – 3
   4x² – 9
2. Water flows from a pipe at the rate of 250 litres per minute. If the pipe used to drain a tank full of water measuring 3.2m by 2.5m by 2m,how many minutes would it take to drain the tank completely. (3mks)
3. Without using tables, solve for a in the equation. ( 3mks)
   Log₃ (2a+8)-log₃9=1+log₃²
4. The base and perpendicular heights of a triangle measured to the nearest centimetre are 6cm and 4cm respectively.
   Find ;
   1. The absolute error in calculating area of the triangle (2mks)
   2. The percentage error in the area giving the answer to 1 decimal place. (2mks )
5. Use logarithms to evaluate
       (0.0056)^1/2  (3 marks)
   (1.38×27.42)
6. Simplify by rationalizing the denominator (2mks)
          3          
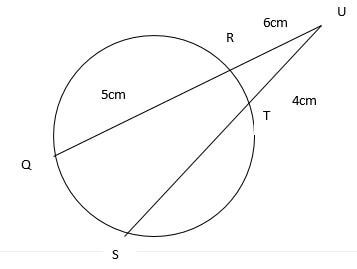
      2√3- √2
7. Chords QR and ST intersect at U.QR =5cm, RU=6cm and TU=4cm. Find the length SU. (3mks)
   
8. A scientific calculator is marked at sh 1560 .Under hire purchase a down payment of sh.200 was paid and six monthly installment of sh 250 each. Calculate;
   1. The Hire purchase price (2mks)
   2. The extra amount paid out over the cash price. (1mk)
9. Make x the subject of the formula. (3mks)
   
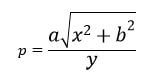
10. The first term of arithmetic is -7 and the common difference is 4.
    1. List the first 6 terms of the sequence. (2mks)
    2. Determine the sum of the first 30 terms of the sequence. (2mks)
11. A small cone of height 8cm is cut off from a bigger cone to leave frustum of height 16cm.If the volume of the smaller cone is 160cm³.Find the volume of the frustum. (3mks)
12. Find the angle Ѳ in degrees from the figure below. (3mks)
    
13. Jane deposited ksh.50,000 in a financial institution in which interest is compound quarterly. If at the end of the second year she received a total of ksh.79,692.40. Calculate the rate of interest per annum. (3mks)
14. ABCDE is a regular pentagon .Its sides AB and DC are produced to meet at T. Calculate the size of angle BTC. (3mks)
    
15. Use reciprocals, cubes and square root . (4mks)
    2 + ³√(20.7726 ) - √0.2643
    0.9272
16. Five men working six hours a day take eight days to fill a trench. How long does it take three men working eight hours a day to complete the same trench. (3mks) 

SECTION II (50 marks)
ANSWER ONLY FIVE QUESTIONS

17. The table below shows how income tax was charged on income earned in a certain year.
    

    Taxable income per year)(Kenya pounds)	Rate (shillings per Kenya pound
    1-3630 3631-7260 7261-10890 10891-14520	2 3 4 5

    Mr.Gideon is an employee of a certain company and earns a salary of ksh 15,200 per month.He is housed by the company and pays a nominal rent of Ksh.1050 per month.He is married and is entitled to a family relief of ksh.450 per month.
    1. Calculate his taxable income in k£ p.a. (2mks)
    2. Calculate his gross tax per month . (4mks)
    3. Calculate his net tax per month (2mks)
    4. Calculate his net salary per month. (2mks)
18.                          
    1. Find the inverse of the matrix (1mk)
       A= (4 3 3 2 )
    2. Rose bought 20bags of oranges and 15 bags of mangoes for a total of ksh.9,500.Chumo bought 30 bags of oranges and 20 bags of mangoes for ksh 13,500.If the price of a bag orange is x and that of mangoes is y.
       1. Form two equations to represent the information above. (2mks)
       2. Hence use the matrix A-1 above to find the price of one bag of each item. (3mks)
       3. The price of each bag of oranges was increased by 10% and that of oranges reduced by 10%.the businesswomen (Rose and Chumo) bought as many oranges and as many mangoes as they bought earlier. Find by matrix method the total cost of oranges and mangoes that the businesswomen bought after the percentage charges. (4mks)
19. A radio dealer planned to buy some radios from a wholesale for ksh.340,000 .Before he could buy them prices of each radio was increased by ksh.300.He now discovers that he can only afford to buy 30 radios less than he had planned to buy with some amount of money. Taking x as the intended number of radios.
    1. write an expression in terms of x for:
       1. original price per radio ( 1mk)
       2. price per radio after the increase (1mk)
    2. determine :
       1. number of radios he had originally planned to buy ( 5mks)
       2. percentage increase in the price per radio (3mks)
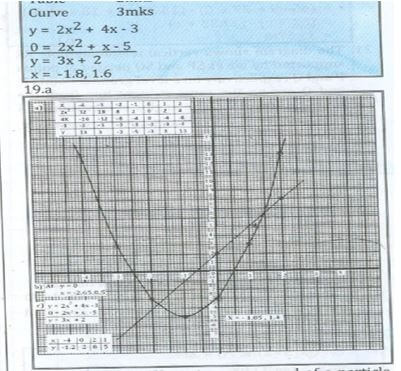
20. Draw the graph of the function y=2x2+4x-3 on the grid provided for -4≤x≤2(2mks)
    
    1.                          
       

       X	-4	-2	-1	0	1	2
       y

       
    2. Use the graph to solve the equation
       2x²+4x-3=0 to 1 decimal place. (2mks)
    3. Use graph y=2x² + 4-3 to solve 0=2x²+ x-5. (3mks)
21. Given that BC is a tangent to the circle and that angle ABC =110º and angle ABC=110º and angle CBD=50º .Calculate giving reasons ;
    1. Angle AED (2mks)
    2. Angle BAD (2mks)
    3. Angle DCB (2mks)
    4. Given that BD = 3cm and DC=5cm.Find the area of triangle BDC. (4mks)
22. The variances p,q and r are such that p varies directly as q and inversely as the square of r.
    1. When p=q,q=12 ,and r=12,find p when q=15 and r=5. (4mks)
    2. Express q in the terms of p and r. (1mk)
    3. If p is increased by 20% and r is reduced by 10%,find:
       1. A simplified expression for the change in q in terms of p and r. (3mks)
       2. Percentage change in q. (2mks)
23. The first ,third and sixth terms of an arithmetic progression (AP) corresponds to the first three consecutive terms of an increasing Geometric progression(G.P).The first term of each progression is 16,the common difference of AP is d and the common ratio of the GP is r.
    1.                              
       1. Write two equations involving d and r. (2mks)
       2. Find the value of d and r (4mks)
    2. Find the sum of the first 20 terms ;
       1. The arithmetic progression (AP). (2mks)
       2. The geometric progression(GP) (2mks)
24. The figure below shows a triangle ABC enclosed in a circle AC=10cm BC=7cm and AB=8cm.
    
    
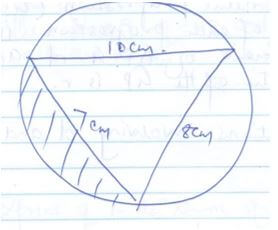
    1. Find the size of angle CAB (2mks)
    2. Find the radius of the circle (2mks)
    3. Hence calculate the area of the shaded region. (6mks)

MARKING SCHEME

1. 2x²+ x-3
   4x² -9
   2x² +3x – 2x – 3
   X(2x +3) -1(2x +3)
   (2x+3) (2x-1)
   4x² – 6x + 6x -9
   Thus (4x²-9) can be written as (2x+3) (2x+3)
   (x-1) (2x +30)
   (2x +3) (2x+3)
   = x - 1
     2x -3
2. Volume = L x w x h
   3.2m x 2.5m x 2m
   =1600m³
   1m³=10001
   1600m³=x
   M³1600 x 1000L = 1,600,000
         1m³                       250
   =6400 MINUTES
3.                           
   
4.                            
   1. 8.5 x 8.5 x 3.25 = 234.8125 cm³ (Greatest)
      7.5 x 7.5 x 3.15 = 177.1875cm³
      8x8x3.2=204.8cm³
      -234.8125cm                    204.8cm³
      
   2. 204.8 -177.1875cm = 27.6125cm³
      30.01cm³
      30.01cm greatest
5.                            
   
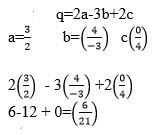
   X² x y²
   6² + 21²
   36 + 441
6. 3(2√(3 ) + 32)
   2√3 - √(2)) (2√3 + √(2))                     6 √3 + 3 √2
                                                                10
   6√(3 ) + 3 √26√3 + 3 √2
   12 + 2 √6 - 2√(6 ) - 2
              10       10
7. QU.RU=SU.TU
   (11x6)=(x+4)4                   m1
   66 = 4x +16
   50=4x
   X=⁵⁰/₄              m1
   =12.5
   SU=12.5 +4            A1
   =16.5
8. Hire purchase price .Down payment =200           m1
   Installment = 6x250= 1500
   1700        m1
   =1700
   - 1560
     140  
9. P=a√x² + b²
   (py)² = (√x²  + b²)²  m1
     a
   P²y²= x² + b²               m1
    a²
   x²=P²y²- b²     m1
          a²
   x= P²y² - √b²
          a
10. Q=-7
    d=4
    n^th term = a +(n-1)d
    = -7,-3,1,5,9,13,17 m1
    Sum = ⁿ/₂(2a + (n-1) d )
    ³⁰/₂ (2(-7) + (30 -1) 4)
    15(-14 +116)
    = 15x102
    =1530
11.                                          
    
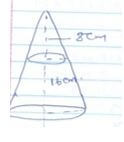
    Volume of cone=⅓πr²
    160cm³ =⅓ x²²/₇ x r² x 8
    r²=(160 x 21)
            (22x 8)
    r²=
12. 2x – 3y + 6=0
    3y=2x +6
    Y=²/₃x + 2
    Gradient, m =tan (180-θ) = ²/₃ B1
    180-θ = tan (²/₃)
    180-θ=33.7º B1
    θ=180-33.7
    =146.3º
13.                                   
    
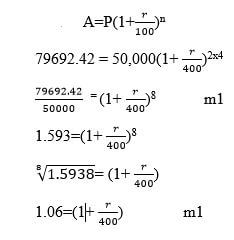
       r   = 0.06
    400
    R=0.06x 400
    =24% A1
14. <CBT = < BCT=360          B1
                               5
    =72º B1
    <BTC =180-(72x2)                m1
    =180-144
    =36º          A1
15.       2           + ∛20.7726 - (26.43 x 10^-2)^½              20.713
    9.072 x 10
        20.571
    =(0.1079 x 10 x 2) + (2.749) – (5.1410)  M1          0.202
                      0.1381
    1.079                           1.158                                    29        
    X 22.749                                                             0.1410
    1.158                          3.907-5.1410        m1
16. Men hours days
     5       6       8
    3        8       -        B1
    5/3 x 6/8 x 8              m1
    =10 days              A1
17.                        
    1. Taxable income =(115/100 x 15,200)= 1050
       = 17480-1050
       =16,630                   m1
       k£ (16,430 x 12) = 9858k£              m1
                     20
    2. 3630 x 2=7260 m
       3630 x 3=10980
       2598 x 4=10392
       Total tax per month =28,542
                                           12
       =ksh.2378.50 B1
    3. Net tax = 2378.50 – 450 m1
       =ksh.1928.50                      A1
    4. Net salary = 15,200-1928.50 -1050                m1
       =12,221.50                 A1
18.                            
    1. Det(4x2)-(3x3)=-1                  B1
       (-2 3 3 -4 )                              B1
    2. 20x + 15y =9500                    B1
       1. 30x + 20y = 13,500          B1
          Divide by 5
       2.  x =(-2 3 3 -4 )(1900)       m1
           y                     1350
       3. (x/y) = (250/200)             m1
    3. 110/100 x 250 = sh.275        m1
       90/100 x 200 = sh.180          m1
       (20 15 15 20 )(215/180)=(8200/11,850)
       =8200+11,850
       Sh.20.050
19. Original price=sh 340,000
    No of ratio=x
    Cost of each radio=sh.340,000
                                           X
    New no of radios = x-30
    New price of radio=340,000   B1
                                      x-30
    340,000 + 300 = 340,000  B1
       X            x-30
    340,000 + 300x = 340,000         m1
                                   x-30             m1
    340,000(x-30)+ 300x(x-30) = sh.340,000    m1
    3400x – 102,000 + 3x²- 90 x=3400 x
    3x²-9x – 102,000 = 0       m1
    X²- 30x-34000=0
    P=3400
    S=-30
    X²-200x+170x-34000=0         m1
    X(x-200) + 170(x-200)=0       B1
    (x+170) (x-200)=0                 A1
    X=200
    New price of radio=340,000    A1
                                     170
    = sh.2000            m1
20.                                
    
21. <AED=180-60
    =120º opposite angles of a cycle quadrilateral
    <BAD = 50º(Alternate segment theorem)
    < DCB =180-(110º+50º)
    =20º(internal angles of a triangle add up to 180º)
    Area of triangle =½ab sin 110º
    =½ x 3 x 5 x sin 110º
    = 21.14cm²
22.                            
    1. P=   kq   m1
              r²
       q=k(12)
           144
       k=144 x 9          m1
              12
       =108
       P=108q = (108)(15)     A1
              r²               5²   
       P=64.8
    2. P=kq 
           r²
       q=pr²    B1
          108
    3. q= 1.2 p x (0.9r²)          m1
                      k
       = 0.972pr²  m1
               k
       0.972pr²  - pr²
                         k
       =-0.028 pr²      A1
                     k
       % = 0.028 x 100
       =-2.8% or reduction by 2.8%
23.                            
    1. a,a+2d, a +5d
        a+2d  = (a+5d) = r    B2
          a         (a+2d )
       (a+2d)²=a(a+5a)
       a² + 4ad + 4d² = a² + 5ad
       4d²= 5ad-4ad
       4d² = ad
        d       d
       a=4d
       r=(a+2d)       m1
             (a )
       r=6d  m1
          4d
       r=1.5
    2.                            
       1. Sn = ⁿ/₂ (2a+(n-1)a)
          ²⁰/₂ (2(16) + (20-1) 4)    m1
          10(32+76)        A1
          10(108)
          =1080
       2. 16 (1.5²⁰- 1) = 106.376.2154 A1
               1.5-1
24.                                        
    1. a² = b² +c² - 2bc cos A
       Cos A=  b²c²a²
                     2bc
       = 10²+ 8²- 7² A1
              2x10x8
       =44.05º
    2.                 7                     2R                
               sin sin 44.05 
                       7                      A1                
               sin sin 44.05
       =5.034
    3. Area of sector 88.1x 3.142 x 5.034²
                              360
       = 19.49cm           A1
       =½ x 5.034² x sin 88.1 m
       =12.66cm² A1
       Shaded area=19.49-12.66 m
       = 6.83cm²            A1