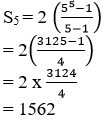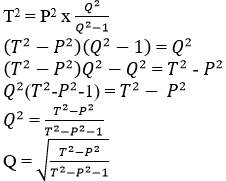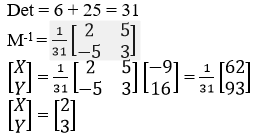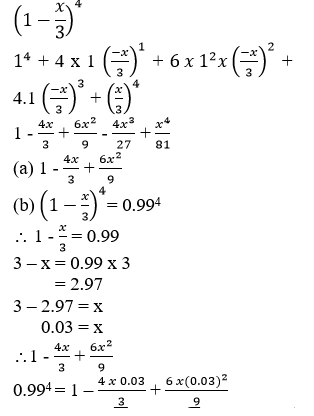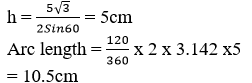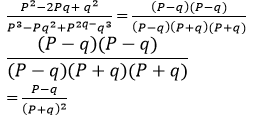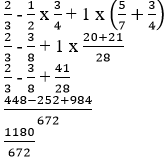QUESTIONS
SECTION 1
- Use logarithm tables to evaluate. (4 Marks)

- Find the sum of the following G.P. (3 Marks)
2 + 10 + 50 + …………… + 1250 - Make Q the subject of the formula. (4 Marks)
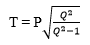
- Chords QR and ST intersect at U. QR = 5cm, RU = 6cm and TU = 4cm.
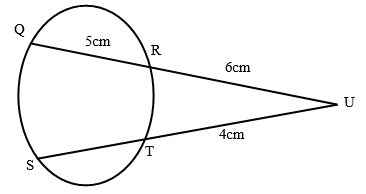
Find the length SU (3 Marks) - Given the matrix m =
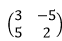 . Find the inverse of m and hence solve the simultaneous equations. (4 Marks)
. Find the inverse of m and hence solve the simultaneous equations. (4 Marks)
3x – 5y = -9
5x + 2y = 16 - Use tables of reciprocals only to work out (3 Marks)
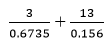
-
- Find the expansion in ascending powers of x of
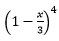 up to the term containing x2. (2 Marks)
up to the term containing x2. (2 Marks) - Use your expansion to find the value of (0.99)4 to four significant figures. (2 Marks)
- Find the expansion in ascending powers of x of
- The diagram below shows a part of a circle centre O with chord AB = 5√3cm and angle AOB = 1200. Find the length of the arc ACB. (Take π = 3.142) (3 Marks)
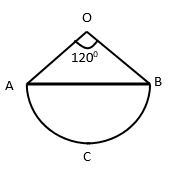
- Simplify (3 Marks)
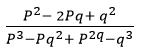
- In the figure below ABCD in a circle with centre O. AB and DC meet a point E outside the circle. DC = BC and ∠BCE = 48º.
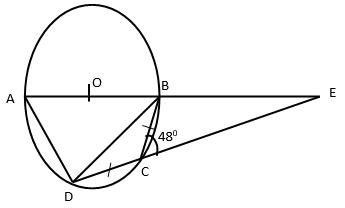
Find the angles:- BAD (1 Mark)
- BDC (1 Mark)
- BEC (1 Mark)
- A Kenyan bank buys and sells foreign currencies as shown.
Buying (KSh.) Selling (KSh.)
1 Euro 81.15 84.26
100 Japanese yen 65.37 65.45
A Japanese travelling from France to Kenya had 5000 Euros. He converted all the 5000 Euros to Kenya shillings at the bank. While in Kenya, he spent a total of KSh. 289850 and then converted the remaining KSh. to Japanese Yen at the bank. Calculate the amount in Japanese Yen that he received. (3 Marks) - The scale of a map is 1:50,000. On the map, the area of Kimalel sub-location is 96cm2. Calculate the actual area of the sub-location in square kilometres (km2) (3 Marks)
- Work out the following
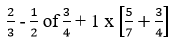 (2 Marks)
(2 Marks) - Given that 4x2 – 32x – 20 + k is a perfect square. Find K. (3 Marks)
- Given the triangle ABC below, AB = 9.2cm AC = 7.9cm and ∠ABC = 480.
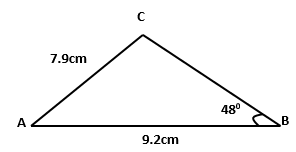
Calculate to 1dp the angle ACB. (2 Marks) - A straight line passes through A (-3, 8) and (3,-4). Find the equation of the straight line through (3, 4) and parallel to AB; giving the answer in the form of y = mx + C. (3 Marks)
- Income tax rate are as shown below.
Omari pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh. 10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine;Income (K£ p.a)
Rate (KSh. per £)
1 – 4200
2
4201-8000
3
8001-12600
5
12601-16800
6
16801 and above
7
- His gross tax p.a. in KSh. (2 Marks)
- His taxable income in K£ p.a. (4 Marks)
- His basic salary in KSh. p.m. (2 Marks)
- His net salary per month. (2 Marks)
- The figure below shows triangle OPQ in which OS = 1/3OP and OR = 1/3 OQ. T is a point on QS such that
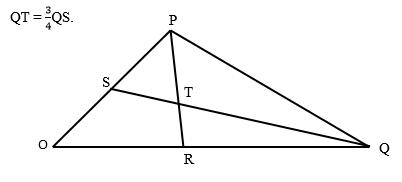
- Given that OP = p and OQ = q: express the following vectors in terms of P and Q.
- SR (1 Mark)
- QS (2 Marks)
- PT (2 Marks)
- TR (2marks)
- Hence or otherwise show that the points P, T and R are collinear. (3 Marks)
- Given that OP = p and OQ = q: express the following vectors in terms of P and Q.
- A slaughter house bought a number of goats at Sh. 2000 each and a number of bulls at Sh. 15000 each. They paid a total of Sh. 190,000. If they bought twice as many goats and three bulls less, they would have saved Sh. 5000.
- Find the number of each type of animals bought. (5 Marks)
- The slaughter house sold all the animals at a profit of 25% per goat and 30% per bull. Determine the total profit they made. (5 Marks)
- The probability that a pupil goes to school by a boda - boda is 2/3 and by a matatu is 1/4. If he uses a boda- boda the probability that he is late is 2/5 and if he uses matatu the probability of being late is 3/10. If he uses other means of transport the probability of being late is 3/20.
- Draw a tree diagram to represent this information. (3 Marks)
- Find the probability that he will be late for school. (3 Marks)
- Find the probability that he will be late for school if he does not use a matatu. (2 Marks)
- What is the probability that he will not be late for school? (2 Marks)
- A tank has two inlet taps X and Y and outlet tap Z. When empty the tank can be filled by tap X in 9 hours or by tap Y alone in 6 hours. When full, the tank can be emptied in 4 hours by tap Z.
- The tank is initially, empty, find how long it would take to fill up the tank;
- If tap Z is closed and taps X and Y open at the same time. (2 Marks)
- If all the three taps are opened at the same time. (2 Marks)
- The tank is initially empty and the three taps are opened as follows:
X at 10.00 a.m.
Y at 10.45 a.m
Z at 11.00 a.m- Find the fraction of the tank that would be filled by 11.00 a.m (3 Marks)
- Find how long it would take for the tank to be filled up (3 Marks)
- The tank is initially, empty, find how long it would take to fill up the tank;
- The distance between two towns A and B is 360km. A bus left town A and travelled towards town B at an average speed of 60km/h. After 11/2 hours, a car left town A and travelled along the same road at an average speed of 100km/h.
- Determine;
- The distance of the bus from town A when the car took off. (2 Marks)
- The distance the car travelled to catch up with the bus. (4 Marks)
- The distance from P to Q is 160km. If an express train was 16km/h slower, it would take 20 minutes longer on the journey. Find the average speed of the express train. (4 Marks)
- Determine;
-
- Find the inverse of matrix below. (3 Marks)
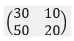
- Mutua bought 30 exercise books and 10 biro pens, while Rose bought 50 similar exercise books and 20 biro pens. Mutua spend 70 shillings while Rose spend 50 spend 50 shillings more than Mutua. Taking the cost of an exercise book to be x and the cost of a biro pen to be y.
- Form two equations connecting x and y to represent the above information. (2 Marks)
- Using matrix method find the cost of each item. (6 Marks)
- Find the inverse of matrix below. (3 Marks)
-
- Triangle ABC has vertices A(2,1) B(4,1) C(3,4). Plot triangle ABC in the grid provided. (2 Marks)
- A'B'C' is the image of ABC under reflection along x-axis. Draw the triangle A'B'C' in the same xes. (2Marks)
- Triangle A''B''C'' is the image of ABC under rotation of negative 90º(-90º) through the origin. Draw the triangle A''B''C'' in the same axes. (2 Marks)
- Triangle A'''B'''C''' is the image of ABC under a rotation of +90º about (0,0). Draw the triangle ABC in the same axes. (2 Marks)
- Describe the transformation that maps A'B'C' onto A'''B'''C''' (2 Marks)
MARKING SCHEME
|
No. |
|||||||
|
1. |
Log 3.846 = 0.5850
|
||||||
|
= 4.5022 |
|||||||
|
2. |
a = 2 |
||||||
|
3. |
Make Q the subject of the formula |
||||||
|
4. |
QU x RU = SU x TU |
||||||
|
5. |
|
||||||
|
6. |
3(0.6735)-1 + 13 (0.156)-1 |
||||||
|
7. |
|
||||||
|
8. |
|
||||||
|
9. |
|
||||||
|
10. |
|
||||||
|
11. |
5000 x 84.15 |
||||||
|
12. |
1cm rep 50,000cm |
||||||
|
13. |
|
||||||
| 14 |
4x2 – 32X – 20 + K = (2x – a)2 |
||||||
| 15 |
9.2 = 7.9 |
||||||
| 16 |
Gradient of AB = Δy |
||||||
| 17 |
|
||||||
| 18 | 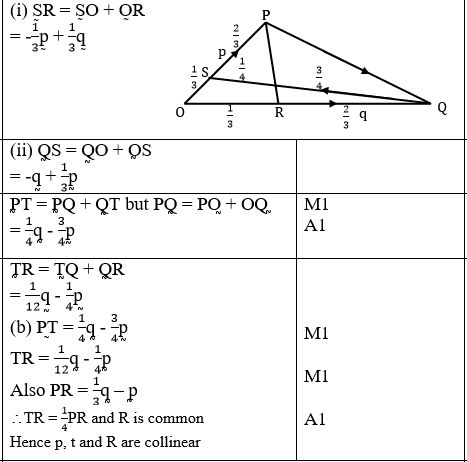 |
||||||
| 19 |
|
||||||
| 20 | 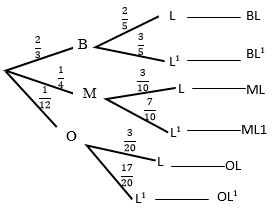 |
||||||
| 23 | 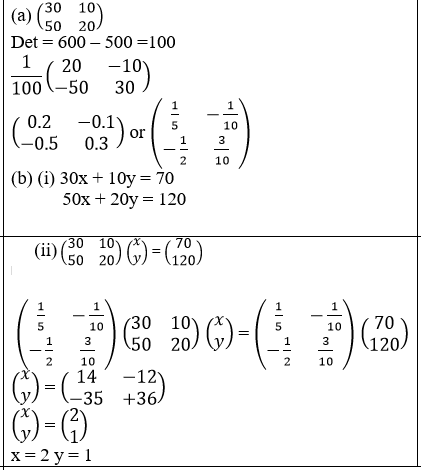 |
||||||
| 24 | 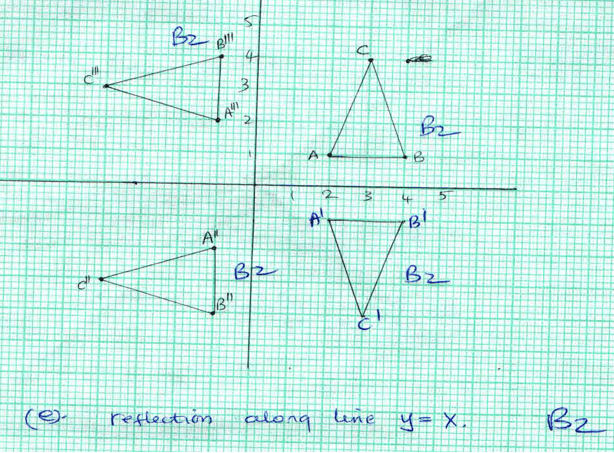 |
||||||
Download Mathematics Paper 2 Questions and Answers - Form 3 End Term 3 2022 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students