Mathematics Questions and Answers - Form 3 Opener Term 1 Exams 2022

MATHEMATICS 

Instructions

• This paper has two sections; section A and section B
• Attempt all the questions in this paper
• Use of calculators and KNEC mathematical tables may be used except where stated otherwise.

Questions

1. Using logarithms tables only, evaluate. (4 Marks)
   
2. Solve the equation (3 Mks)
   x-2 - 3-x = x-2
     3      4       2
3. A tourist arrived in Kenya with sterling pound (€) 4680 all of which he exchanged into Kenyan shillings. He spent ksh. 52,352 while in Kenya and converted the rest of the money into US dollars. Calculate the amount he received in US dollars. The exchange rates were as follows. (3mks)
   Currency                      Buying              Selling
   USṨ                              65.20               69.10
   Sterling pound €          123.40             131.80
4. Solve for the value of x (3Mks)
   2^3x-2 × 8^x = 4^(x+1)
5. A line passes through the point whose coordinates are A(1,3) and B (-2,-1) find the equation of the line (3 Mrks)
6. Express as a fraction. (3mks)
7. Use reciprocal and square tables to evaluate, to 4 significant figures, the expression. . (3Marks)
       1     – 4.151²
   0.3654
8. The diagonal of a square measures 44cm.Calculate the perimeter of the square. 3mrks
9. Calculate; [3mks]
   2.61 x 21.83 x 0.073
       61.72 x 11.73
10. Patrick spent 2/5 of his salary on food, 1/3 of the remainder on electricity and saved the rest.
    1. What fraction of his salary did he save? (2mrks).
    2. If he spent Sh. 1,200 on food, how much did he spend on electricity? (2Mks)
11. Solve the following simultaneous equation (3 Mks)
    5x+6y=28
    3x+4y=18
12. Two similar containers have base areas of 750 cm2 and 120cm2 respectively. Calculate the volume of the larger container in liters given that the volume of smaller container is 400 cm3 (3 Mrks).
13. If r=5, s=2, and t=3, find the value of; (3mks)
       r²+s²-t
         t³
14. A farmer has three containers of capacity 12L, 15L and 21L, calculate the capacity of:
    1. The smallest container which can be filled by each one of them an exact number of times (2 Mrks).
    2. The largest container which can fill each one of them an exact number of time.(2 Mks)
15. Given that tan x = ¾, find Cos(90-x) (2 Mks).
16. The two arms of a pair of compass of dividers are spread so that the angle between them is 45°.Find the area of the sector formed if the length of the arm is 8.4cm.Take π = ²²/₇.(3marks)

SECTION II (50 MARKS)
ANSWER ALL QUSTIONS

17. An amount of money was shared among five girls, Alice, Jane, Brenda, Mary and Ivy. Alice got ¹/₈ of the total amount while Jane got ²/₅ of the remainder. The remaining amount was shared equally among Brenda, Mary and Ivy each getting ksh.490.
    1. How much did Jane get? (3mks)
    2. How much was shared among the three girls. (3mks)
    3. Alice, Jane and Ivy invested their money and earned a profit of ksh.3640. a half of the profit was left to maintain the business and the rest shared according to their investments. Calculate how much each got. (4mks)
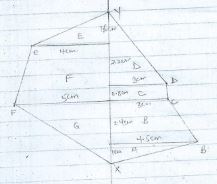
18. A surveyor recorded the measurements of a field book using xy=400m as the base line as shown below
                                    Y
       To E 200             320
                                  210               150 To D
       To F 205             170               150 To C
                                     50               225 To B
                                    X
    1. Use a scale of 1 cm to represent 50 m to draw the map of the field. (5 Mks)
    2. Find the area of the field in hectares (5 Mks)
19.     
    1. On the grid provided, draw the square whose vertices are A(6,-2) B(7,-2) C(7,-1) and D(6,-1). (2mrks)
    2. On the same grid draw;
       1. A’B’C’D’, the image of ABCD under an enlargement scale factor 3centre (9,-4). (4mrks)
       2. A”B”C”D”, the image of A’B’C’D’ under a rotation of +900 about (0,0). (4 mrks)
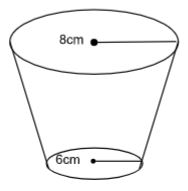
20. A pail is in the shape of a container frustrum with base radius 6cm and top radius 8cm. The slant height of the pail is 30cm as shown below. The pail is full of water.
    
    
    1. Calculate the volume of water in the pail. (6mks)
    2. All the water is poured into a cylindrical container of circular radius 7cm, if the cylinder has the height of 35cm, calculate the height of the cylinder above the water level, which is not in contact with water. (4mks)
21. The sides of a triangular plot of land are 170m, 190m and 210m, but the altitudes of the plot as well as the angles are not known. Find
    1. The area of the plot in Hectares 5mks
    2. The angles of the plot 5mks

Marking Scheme

1.     
   

   No	log
   849.6   2.41	2.9292 0.3820
   3941	3.3112 3.5956
   	1.7156 ÷       3
   	1.9052
   = 8.039 x 10-1 = 0.8039

2.   (^x-2/₃)¹² - (^3-x/₄)¹² = (^x-2/₂)¹²
   4x - 8 - 9 + 3x = 6x -12
   7x -17 = 6x 02
   7x -6x = 17-2
   x=5
   
   
3. £ 4680 x 123.40 = 577512
   spent  → 52352
   Balance = 525160
   525160 = 7600
     69.10
   US Dollar = 7600
   
   
4. 2^3x-2 x 2^3x = 2^2(x+1)
   2^3x-2 x 2^3x = 2^2x+2
   2^3x-2+2x = 2^x+2
   6^x-2= 2^x+2
   4x =  4
    2      4
   x=1
   
   
5. G= ΔY/ΔX 
   =    1-3    =  -4  =    4  
         -2-1        -3       3
   Taking a point A(1,3)
   and (x,y)
    4  =    y-3  
    3        x-1
   4(x-1) = 3(y-3)
   4x-4= 3y-9
   y= ^4x/₃ + ⁵/₃
   
   
6. Let 1.523523 be r
   1523.523...= 1000r
   1000r = 1523.523523...
       r    = 1.523523...
   999r = 1522
    r = 1522/999
   1 523/999
   
   
7. ¹/_0.3634 - 4.151^{2
   1}/_0.3654 → 2.737
   4.151² → 17251
   2.737 - 17.251
   = -14.494
   
   
8. 44² = x² + x²
   44² = x²
   1936 =  2x²
     2          2
   x= 968
   x= 31.11
   P = L+L+L+L
   = 31.11 x 4
   1245.45cm
   
   
9. 2.61 x 21.83 x 0.073 x 10⁷
         61.72 x 11.73  10⁷
   = 0.00575
   
   
10. Food=²/₅
    Electricity = 1 - ²/₅ = ³/₅ x ¹/₃ - ¹/₅
    Savings = 1 - {²/₅ + ¹/₅}= ²/₅
    ²/₅ → 1200
    ¹/₃ →
    ¹/₅ x 1200
     ²/₅
    = Sh. 600
    
    
11. ( 5x + 6y = 28) 3
    (3x + 4y = 18 )5
    15x + 18y = 84
    15x + 20y =90
     -2y = -6
         y=3
    5x + 18 =28
    5x + 10
    x=2
    y=3, x=2
    
    
12. A.S.F = 750/120 = 25/4
    L.S.F = √²⁵/₄ = 5/2
    V.S.F = 125/8
       V₁   = 125
     400       8
     V₁ = 400 x 125 =  6250
               8                1000
    6.25 Litres
    
    
13. 5² + 2² - 3 = 25 + 4 - 3
      3³                   27
    = ²⁶/₂₇
    
    
14.          
    1. L.C.M of 12,15 and 21
       = 420
    2. G.C.D = 12, 15 and 21= 3
15.  2 > 3-x > 5
    2> 3-x
    x>3-2  → x>1
    3-x > 5
    -x <5 -3 → +x<2
    x<2
    1< x < 2
    
    
16. ⁴⁵/₃₆₀ x ²²/₇ x 8.4 x 8.4
    1/8 x 22 x 1.2 x 8.4
    = 27.72
    
    
17.            
    1. Alice = 1/8
       Jane 2/5 of ( 1 -1/8) = 7/20
       Brenda, Mary , Ivy - @ 490 x 3 = 1470
       21/40
       21/40 → 1470
        7/20  → ?
       1470 x ⁷/₂₀
           ²¹/₄₀
       Jane = Ksh 980
       
       
    2. Amount shared
       = 490 x 3= 1470
       
       
    3. Alice amount = 1/8 x 2800 = 350   -- 1820
       Ivy                 →                    490 
       Jane              →                    980 
       Profit shared = 3640 = 1820
                                  2
       Alice =    350    x 1820 = 350
                    1820
       Jane   980   x 1820 = 980
                1820
       Ivy =    490   x 1820 = 490
                1820
18.               
    1.    
       
       
       
    2. A - Right angled Δ.A= 1/2bh = 1/2 x 184.5 = 2.25cm²
       B - TRapezeur = 1/2(A+B)h = 1/2 x (3+45)2.4 = 9cm²
       C - Rectangle = LxW = 0.8 x 3= 2.4cm²
       D - Right- angled Δ = 1/2 x 3 x 3.8 = 5.7 cm²
       E - ..... = 1/2 x 1.6 4 = 3.2cm²
       F Trapezium = 1/2(5+4)3 = 13.5cm²
       G Right Angled Δ = 1/2 x 3.4 x 1 = 8cm²
       Total area = 44/55cm²
       1cm rep 50m = 11135m² = 11.1375ha
                                 10000
19.                 
    1.   
       
       
       
20.                    
    1. 8/6 = 30 + x
                    x
       8x = 180 + 6x
       2x = 180
       x= 90cm
       h= 90² - c²
       h= 89.80cm
       H² = 120² - 8²
       H= √1400 - 64
       V₁ = ¹/₃ x ²²/₇ x 8 x 8 x 119.25 = 8027.61
       V₂ = ¹/₃ x ²²/₇ x 6 x 6 x 89.80 = 3386.74
       Volume of the frustrum = V₁ - V₂
       = 8027.61 - 3386.74
       = 4640.87cm³
       
    2. V= 4640.87
       V of the cylinder = πr2h
       ²²/₇ x 7 x 7 xh = 4640.87 cm²
       h= 4640.87 = 30.14cm
                154
       35cm - 30.14
       = 4.86cm 
               
21.                      
    1. A = √s(s-a)(s-b)(s-c)
       s= 1/2(120 + 190 + 210) = 285
       A=√285(285-210)(285-190)(285-190)
       A= √285(75)(95)(115)
       A = √233521875
       = 15281.42255m²
                  10,000
       1.528ha
       
       
    2. A= 1/2abSinC
       Sin C = Area =         15281.42      
                    ¹/₂ab    ¹/₂ x 210 x 190
       Sin C = 0.76598
       <C = 49.99°
       Sin B =    Area   
                    1/2 ac
       =         15281.42         = 0.8561
            1/2 x 210 x 170
       <B = 58.88°
       <A = (180) - (4999 + 58.88°)
       = 71.13°