Mathematics Questions and Answers - Form 3 Mid Term 1 Exams 2022

Questions

SECTION I (20MKS):
Answer all questions in this section in the spaces provided

1. Evaluate;
   1. Sin ²/₃π^c (2mks)
   2. Tan 1.2^c(2mks)
2. If log₂x + log_x2 = 2, find x. (3mks)
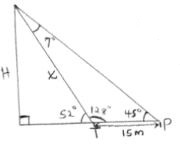
3. The angle of elevation of the top of a building from a point P is 45^o. From another point T, 15 meters nearer the foot of the building, the angle of elevation of the top of the building is 52^o. Calculate the height of the building (correct to 1 decimal place). (4mks)
4. Given that the dimensions of a rectangular book cover are 20.2 cm and 25.0 cm. Find the percentage error in calculating the area (correct to 2 decimal places). (3mks)
5. Simplify by rationalizing the denominator: (3mks)
      2   
   4-√5
6. Use the method of completing the square to solve for x
   4x² + 12x - 9=0 (3mks)

SECTION II (30 MKS): Answer any 3 questions in this section

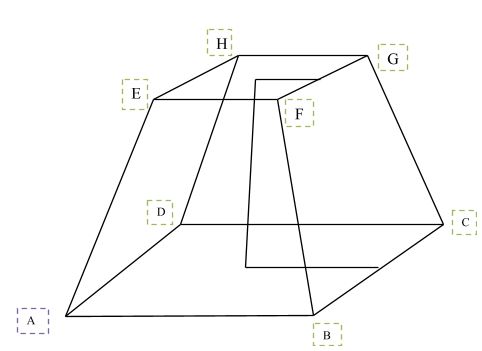
7. The figure below represents a frustum of a right pyramid on a square base. The vertical height of the frustum is 3 cm. Given that EF = FG = 6 cm and that AB = BC = 9 cm.
   
   Calculate correct to 2 decimal places;
   1. The vertical height of the pyramid. (2mks)
   2. The surface area of the frustum. (4mks)
   3. Volume of the frustum. (4mks)
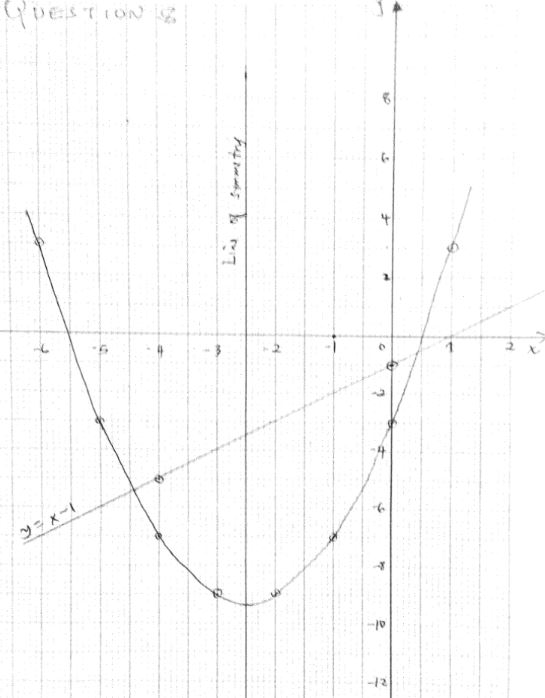
8. Complete the table below for the function y=x2+5x-3 (2mks)
   

   X	-6	-5	-4	-3	-2	-1	0	1
   X2	36			9		1		1
   5X	-30		-20				0
   -3	-3	-3			-3	-3
   Y	3	-3	-7		-9		-3	3

   
   
   1. On the grid provided, draw the graph of y=x² + 5x - 3 (3mks)
   2. State the equation of the line of symmetry for the graph (1mk)
   3. Use the graph to solve the equations;
      1. x²+5x-3=0 (1mk)
      2. x²+4x-2=0 (3mks)
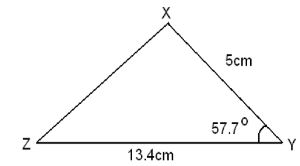
9. The figure below is a triangle XYZ. ZY = 13.4cm, XY = 5cm and angle xyz = 57.70
   
   Calculate
   1. Length XZ. (3mks)
   2. Angle XZY. (2mks)
   3. If a perpendicular is dropped from point X to cut ZY at M, Find the ratio MY:ZM (3mks
   4. Find the area of triangle XYZ. (2 mks)
10.        
    1. Complete the table below by filling in the blank spaces. (2mks)
       

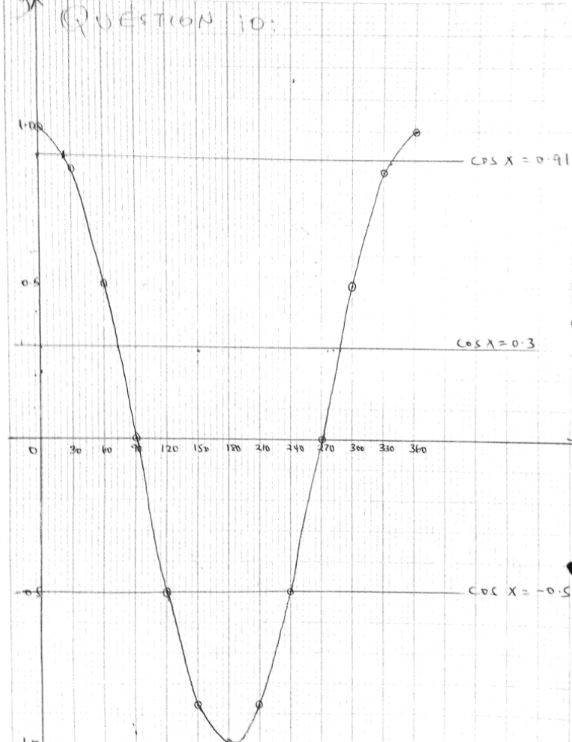
       x

       0°

       30°

       60°

       90°

       120°

       150°

       180°

       210°

       240°

       270°

       300°

       330°

       360°

       Cos x

       0.87

       -0.5

       1.0

       0.00

       0.87

    2. On the grid provided, draw the graph of y = Cos x for 00 ≤ x ≤3600 (5mks)
       (Take the scale: 1cm for 300 on the x-axis and 4 cm for 1 unit on the y-axis).
    3. Use the graph in (b) above to solve the following;
       1. Cos x = 0.91
       2. Cos x = -0.5
       3. Cos x = 0.3 (3mks)
11. A truck left town P at 8:00 a.m and traveled towards town Q at an average speed of 80km/h. At 8.30a.m, a van left town Q towards town P at an average speed of 120km/hr. Given that the distance between the two towns is 400km, Calculate:-
    1. The time the van arrived in town P (2mks)
    2. The time the two vehicles met (4mks)
    3. The distance from town P to the meeting point
    4. The distance of the truck from town Q when the van arrived in town P

Marking Scheme

1.        
   1. π^c = 180°
      2/3 x 180° =120°
      Sin 120° = Sin 60°
      = 0.8660
      
      
   2. 1c = 57.29°
      1.2c = 1.2 x 57.29
                        1
      = 68.748°
      tan 68.758° = 2.5712
      
      
2. Log _x 2 = 1 / Log₂x
   Log ₂ x + 1/ Log ₂ x = 2
   Let Log₂x be y
   y + ¹/_y=2
   y2 + 1 = 2y
   y2 - 2y + 1=0
   y2 -y-y+1=0
   y(y-1)-1(y-1)=0
   (y-1)(y-1)=0
   y=1
   by Log₂x = y
   :Log₂x = 1
   2¹ = x
   x=2
   
   
3.      
    
     15     =      x      
   Sin 7°      Sin 45°
   x = 15Sin45°
           Sin 7°
   = 87.0m
   Sin 52° = H/ 87.0
   H = 87 Sin 52°
   = 68.6m
   
   
4.  The sum of R.E
   Absolute error= least unit of measurement
                                           2
   = 0.1 = 0.05
        2
   R.Erros are ^0.05/_20.2 and ^0.05/_25.0
   R.E in the product 
   =   0.05  +   0.05  
       20.2         25.0
   = 0.002475 + 0.002
   = 0.004475
   %age error = 0.004475 x 100
   =0.4475%
   
   
5.         2         .   4 + √5
     4 -  √5           4 + √5
         2(4 + √5)    
   (4 - √5)(4 + √5)
              8+2√5             
   16 + 4√5 - 4√5 + √25
   8 + 2√5
     16+5
   8+2√5
      21
   
   
6. 4x² + 12x -   9  =   0  
    4        4        4       4
   x² + 3x - ⁹/₄ =0
   x² + 3x =⁹/₄
   x2 + 3x + (³/₂)2 = ⁹/₄ + (³/₂)²
   (x + ³/₂)² = ⁹/₄ + ⁹/₄
   x+³/₂ = ±√¹⁸/₄
   x + ³/₂ = 2.121
   x= 2.121 - ³/₂
   or
   x= -2.121 - ³/₂
   x= 0.62 or -3.621
   
   
7.          
   1. E.S.F = 9/6
      ⁹/₆ = x+3
                  x
      9x = 6x + 18
      3x=18
      x=6cm
      H= 3+6=9cm
      VN = (√(4.5² + 4²))
      = 10.06cm
      VM = (√(8² + 6²))
      = 6.71cm
      Slanting: (1/2 x 9 x 10.6 - 1/2 x 6 x 6.71)4
      (47.7 - 20.13)4
      = 110.28cm²
      
      
   2. Top SA = 6 x 6 = 36cm²
      Bottom SA = 9x9 = 81cm²
      TSA = 110 + 36 +81 = 227.28cm²
      
      
   3. Vol 1/3 x 9x9x9 - 1/3 x 6 x 6x 6
      243 -72 = 171cm³
8.          
   

   X	-6	-5	-4	-3	-2	-1	0	1
   X2	36	25	16	9	4	1	0	1
   5X	-30	-25	-20	-15	-10	-5	0	5
   -3	-3	-3	-3	-3	-3	-3	-3	-3
   Y	3	-3	-7	-9	-9	-7	-3	3

           
   1.        
      
      
      
   2. x= -2.5
   3.          
      1. x = -5.5 or x=0.5
      2.  y = x² + 5x -3
         0 = x² + 4x -2
         y = x-1
         

         X	0	3	-4
         y	-1	2	-5

         
         x=4.4 or x=0.4
9.                     
   1. (XZ)² = 13.4² + 5² - 2 x 13.4 x 5 Cos 57.7 = 204.56 - 71.60 = 132.96
      
      
   2. X2 = √132.96 = 11.53cm
      <xzy →     5    =      11.53    
                     Sin θ     Sin 57.7
      Sin  θ = 0.3665
       θ = Sin^-1 0.3665
       θ = 21.5°
      
      
   3. MV → Cos57.7 = MY/5 →  MY = 5 Cos57.7 = 2.67cm
      ZM → Cos 21.5 = ZM/11.53 → ZM = 11.53 Cos 21.5= 10.73
      MY:ZM = 2.67:10.73 = 267:1073
      
      
   4. Area = 1/2 x 13.4 x 5 Sin 57.7 = 28.31cm²
10.             
    1.      
       

       x	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°	360°
       Cos x	1.0	0.87	0.5	0	-0.5	-0.87	-1.0	-0.87	-0.5	0.00	0.5	0.87	1.0

        
    2.      
       
       
       
    3. Cos x = 0.91   x =24 and 336°
       Cos x = -0.5 x 120° and 240°
       Cos x = 0.3 x 72° and 288°
11.                  
    1.      
       
       Van → time = Distance  =  400km   = 3hr 20min
                                 speed      120km/h
       time arrived ar P = 8:30
                                   +3:20
                                   11:50am
       
       
    2. Distance covered by 8:30 = 80 x 1/2 = 40km
       Remaining distance = 400 - 40 = 360km
       Relative speed = 120 + 80 = 200km/h
       time taken to meet = 360/200 = 1hr 48min
       Time they met:
       8:30am
       1:48       
       10:18am
       
       
    3.  from 8:30 am, truck covers:
       80km/h x 1.8hrs
       =144km
       Distance from town P to meeting
       144 + 40= 184km
       
       
    4. Time the truck travels by the time the van arrives
       3hrs 20 mi + 30 min
       3hr 50 mins
       Distance travelled in 3hrs 50 min
       D= 80 x 3.833hr= 306.64km
       Distance of truck from town Q
       400km- 306.64km= 93.36km