Mathematics Paper 1 Questions and Answers - Form 3 End Term 1 Exams 2022

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Form 3 End Term 1 Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

SECTION A: ATTEMPT ALL THE QUESTIONS

Evaluate
(32÷4 of (-4)×6+28) (4mks)
-40÷5×2
The angle of depression of a hen on a horizontal surface on the ground to a crow perched on top of a building is 28 degrees. The building is 8m tall vertically. When the hen sees the crow, the hen moves directly towards base of the building to a point such that the angle of elevation of the cow from B is 32⁰.
Calculate the distance hen moved. (3mks)
Simplify the expression. (3 marks)
15a²b - 10ab²
3a²-5ab+2b²
The position vectors of points P and Q are
$1$
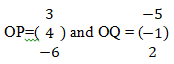
Find the position vector of point X, which divides line PQ internally in ratio, 2:3 (3mks)
Three Villages X,Y and Z are such that y is 12 km south of X and Z is 15km from X..Village. Z is on a bearing of 330º from Y. Calculate the bearing of Z from X. (3mks)
A line AB is formed by coordinates A (1,2) and B (4,6). Another line 2 is the perpendicular bisector to line AB/. Find the equation of line 2. (3mks)
Ann bought four pens and three exercise books for a total of sh.17 while peter bought five pens and two similar pens and two exercise books for a total of sh.16.
Find the cost of a pen and an exercise book (3mks)
Three villages are situated such that they form 3 sides of a triangle. The distance of villages P to R is 40km while R to Q is 60km.When represented on a paper angle PRQ is 78º.Find the distance of village P to Q. (4mks)
A water tank is cylindrical in shape is filled by a pipe p in 6 hours. This same tank is emptied when filled in 12 hours by a pipe. When someone starts with the tank empty, both pipes are opened at the same time and then pipe Q turned off after 4 hours. Find the time taken to fill the tank. (3mks)
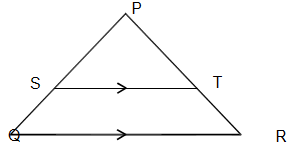
The figure below shows triangle PQR in which PR = 12cm. T is a point on PR such that TR =4cm. Line ST is parallel to QR. If the area of triangle PQR is 336cm². Find the area of the quadrilateral STQR. (4 marks)
$2$
Kamau spent ³/₅ of his money on buying food,and ½ of what was left on rent.After that,he finds that he has sh.1400 left in his pocket. Determine the amount money spent on buying food. (3mks)
Find the centre of enlargement if P(0,-1) is the image of P(2,3) under enlargement scale factor 3 (3mks)
Use the reciprocal tables to evaluate to determine 3 decimal places, (4mks)
2 - 3
0.4821 24.71.
A bank in Kenya buys and sells foreign currencies as follows.
Currency Buying (Ksh) Selling (Kshs)
1 Sterling pound 134.20 134.65
1 US dollar 71.40 71.84
A tourist arrived in Kenya with $4500. He converted al the dollars to Kenya shillings at the bank, while in Kenya he spend Kshs 215,000 and then converted the remaining amount in Kenya shillings to sterling pound.
Calculate the amount he received in sterling pound. (3mks)
Three students shared a certain amount of money. The first got sh.120 more than the second thrice what the third student got. If the second got sh.300, how much did each of the other two get? (3mks)
In the figure below, BT is tangent to the circle at B. AYCT and BYD are straight lines. AY=6cm, CT=8cm, BY=4.8cm and YD = 5cm
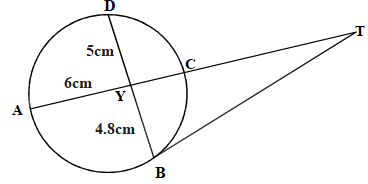Find length of:
1. CY
2. BT

SECTION B: ATTEMPT ANY FIVE QUESTIONS IN THIS SECTION

Three points P, Q and S are pm the vertices of a triangular plain field. P is 400m from Q on a bearing of 3000 and R of 550m directly south of P.
1. Using a scale of 1 cm to represent 100m on the ground, draw a diagram to show the position of the points. (3mks)
2. Use the scale drawing to determine;
  1. The distance and bearing of Q from R. (3mks)
  2. The bearing and distance of point S from P given that point S is directly 600m East of R. (3mks)
  3. The bearing and distance of Q from S. (3mks)
A bus travelling at a speed of 80km/hr left Mombasa at 8.00am for Nairobi. Two hours later, a car travelling at a speed of 100km/hr left Nairobi for Mombasa.
Given that the distance between both cities is 500km, find the: -
1. distance covered by bus at the time the car is starting. (1mk)
2. Distance between the two vehicles at the time the is starting (1mk)
3. Relative speed of the two vehicles (1mk)
4. Time taken for the two vehicles to meet (2mks)
5. Time the met. (1mk)
6. After meeting, the speed of both vehicles dropped to 60km/hr due to traffic jam. At what time did each vehicle arrive at its destination? (3mks)
The kite shown on the fig below has vertices, A(-2,4)B(5,7)C (7,4) D(5,1).The kite ABCD is rotated about the origin through -90º to obtain its first image A’B’C’D’.The kite A’B’C’D’ is then reflected along the line = X = 0 to obtain A”B’’C’’D’’.Find
1. The equation of the Mirror line that reflects point A to itself, B on to D and C onto itself
2. Draw a kite A’B’C’D and state its coordinates.
  $4$
A given solid is made up of a cone and three quarters of hemisphere as shown in the diagram below .The radius and vertical height of the cone are 4cm and 6.2 cm respectively
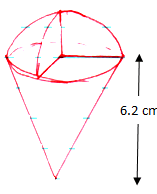
1. Calculate the volume of the solid (4mks)
2. Calculate the surface area of the solid (4mks)
3. The material used for making the solid costs shs 40 per cm3.What is the cost of making ten such solids (2mks)
In the diagram below, two circles, centres A and C and radii 7cm and 24cm respectively intersect at B and D. AC = 25cm.
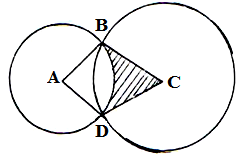
1. Find angle ABC = 90º. (3mks)
2. Calculate
  1. the size of obtuse angle BAD (3mks)
  2. the area of the shaded part (4Mks)
3. Find the area of the farm in hectares (3mks)
4. Karis wishes to irrigate his farm using a sprinkler machine situated in the farm such that it is equidistant from points A, B and C.
  1. Calculate the distance of the sprinkler from point C. (2 Marks)
  2. The sprinkler rotates in a circular motion so that the maximum point reached by the water jets is the vertices A, B and C. Calculate the area outside his farm that will be irrigated. (3 Marks)
Two lines L1=2y-3x-6 and L2=3y+x-20=0 intersect at point A.
1. Find the coordinates of A (3marks)
  1. A third line L₃ is perpendicular to L2 at point A. Find the equation of L₃ in form of y=mx+c, where m and c are constants. (3marks)
2. Another line L₄ is parallel to l1 and passes through (-1,3). Find the x-intercept and the y-intercept of L₄. (4marks)
1. PQRS is a quadrilateral with vertices P(1,4), Q(2,1), R(2,3) and S(6,4). On the grid provided, plot the quadrilateral. (2mark)
2. Draw P’Q’R’S’ the image of PQRS under a positive quarter turn about the origin and write down its co-ordinates. (3 marks)
3. Draw P”Q”R”S” the image of P’Q’R’S’ under an enlargement scale factor -1 and center (0,0) and write down its co-ordinates. (3 marks)
  $4$ Determine the single transformation that maps PQRS onto P”Q”R”S (2marks)
The heights of 40 pupils in a class were measured to the nearest centimeter and recorded as below.
175 154 157 180 165 150 152 162
173 168 169 181 177 179 175 169
151 153 156 158 163 169 179 180
145 149 150 156 171 175 176 178
169 160 155 174 170 176 182 170
1. Use the class interval of 5 to group the data start from 145-149, 150 - 154 . . . (3 marks)
2. Estimate the mean (4 marks)
3. Calculate the median height of the class. (3 marks)

MARKING SCHEME

SECTION A: ATTEMPT ALL THE QUESTIONS

Evaluate
(32÷4 of (-4)×6+28) (4mks)
-40÷5×2
32 ÷ 16 x 6 + 28
- 8 - 2
-2 x 6 + 28
-16
(-12 x 28)
-16
=(¹⁶/_-16)
= -½
The angle of depression of a hen on a horizontal surface on the ground to a crow perched on top of a building is 28 degrees. The building is 8m tall vertically. When the hen sees the crow, the hen moves directly towards base of the building to a point such that the angle of elevation of the cow from B is 32⁰.
Calculate the distance hen moved. (3mks)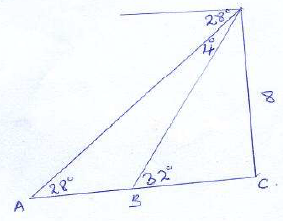
$7$ Tan28 = 8
AC
AC = 8
tan28
= 15.045
BC = 8
Tan32
= 12.803
AB = 2.242m
Simplify the expression. (3 marks)
15a²b - 10ab²
3a²-5ab+2b²
Numerator
5ab(3a - 2b)
5ab (3a - 2b)
(3a - 2b)(a -b)
Denominator
3a²-3ab-2ab+2b²
(3a - 2b)(a -b)
=5ab
a-b
The position vectors of points P and Q are
$1$
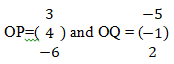
Find the position vector of point X, which divides line PQ internally in ratio, 2:3 (3mks)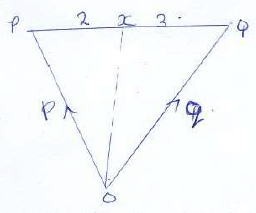
$8$ $19$
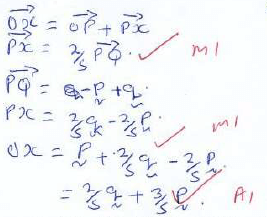
Three Villages X,Y and Z are such that y is 12 km south of X and Z is 15km from X..Village. Z is on a bearing of 330º from Y. Calculate the bearing of Z from X. (3mks)
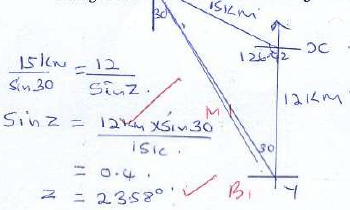$9$ 30 + 23.58 = 53.58
180 - 53.58 = 126.42
Bearing of Z from X is
180º + 126.42 = 306.42º
A line AB is formed by coordinates A (1,2) and B (4,6). Another line 2 is the perpendicular bisector to line AB/. Find the equation of line 2. (3mks)
h. of AB = 6 - 2
4 -1
= ⁴/₃
Line 2 M₁ x M₂ = -1
¾M₂ = -1
M₂ = - ⁴/₃
Mid AB = 1 + 4 , 6 + 2
2 2
(2.5, 4)
y - 4 = -¾
x - 2.5
4(y - 4) = -3x + 7.5
4y = 3x + 23
Ann bought four pens and three exercise books for a total of sh.17 while peter bought five pens and two similar pens and two exercise books for a total of sh.16.
Find the cost of a pen and an exercise book (3mks)
4x + 3y = 17 x 2
5x + 2y = 16 x 3
8x + 6y = 34
15x + 6y = 48
7x = 14
x = 2

8 + 3y = 17
3y = 9
y = 3
Pen costs 2 shillings
Exercise book costs 3 shillings
Three villages are situated such that they form 3 sides of a triangle. The distance of villages P to R is 40km while R to Q is 60km.When represented on a paper angle PRQ is 78º.Find the distance of village P to Q. (4mks)
$10$
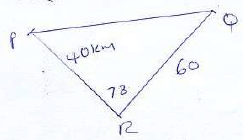
Cosine rule a² = b2 + c² - 2bcosA
(PQ)² = 40² + 60² - 240 .60cos78
= 1600 + 3600 - 4800 x 0.2079
= 5200 - 997.97
= 4202km
PQ = √4202 = 64.82
A water tank is cylindrical in shape is filled by a pipe p in 6 hours. This same tank is emptied when filled in 12 hours by a pipe. When someone starts with the tank empty, both pipes are opened at the same time and then pipe Q turned off after 4 hours. Find the time taken to fill the tank. (3mks)
P = ¹/₆ E = ¹/₁₂
¹/₆ - ¹/₁₂= ¹/₁₂x 4
= ⁴/₁₂
⁷/₁₂÷ ¹/₆
⁷/₁₂÷ ⁶/₁= 6.5h
Time taken
4 + 3.5 = 7½
The figure below shows triangle PQR in which PR = 12cm. T is a point on PR such that TR =4cm. Line ST is parallel to QR. If the area of triangle PQR is 336cm². Find the area of the quadrilateral STQR. (4 marks)
$11$
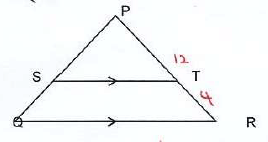
16:12
LSF 4:3
ASF = 16:9
Area of PST 16 ⇒ 336
336 x 9 = 189
16
Area of STRQ = 336 -189
= 147cm²
Kamau spent ³/₅ of his money on buying food,and ½ of what was left on rent.After that,he finds that he has sh.1400 left in his pocket. Determine the amount money spent on buying food. (3mks)
Food = ³/₅
Rent = ²/₅ x ½
= ¹/₅
¹/₅x = 1400
Food = 1400 x 3
= 4800 shillings
Find the centre of enlargement if P(0,-1) is the image of P(2,3) under enlargement scale factor 3 (3mks)
$12$
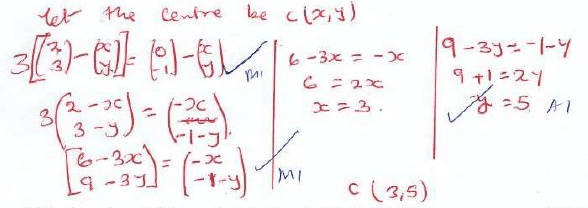
Use the reciprocal tables to evaluate to determine 3 decimal places, (4mks)
2 - 3
0.4821 24.71.
2( 1 ) - 3( 3 )
4.821 x 10¹ 2.471 x 10¹
2(0.2074 x 10) - 3(0.407 x 10^-1)
4.148 - 0.12141
4.02659
Three students shared a certain amount of money. The first got sh.120 more than the second thrice what the third student got. If the second got sh.300, how much did each of the other two get? (3mks)
If the second got sh x then the first got sh(x + 120)
3rd got sh(x + 120)
3
Then x = sh300
1st got 420 x ¹/₃ = 140
In the figure below, BT is tangent to the circle at B. AYCT and BYD are straight lines. AY=6cm, CT=8cm, BY=4.8cm and YD = 5cm

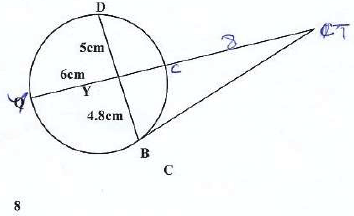
Find length of:
1. CY
  4.8 x 5 = 6 x CY
  CY = 4
2. BT
  BT² = AT x CT
  = 18 x 8
  = 144
  BT = 12
Use the method of completing the square to solve for xo(3 mks)
4x² + 12x - 9 = 0
15ab² - 10ab²
3a² - 5ab + 2b²
Num
5ab(3a - 2b)
Den
3a² - 3ab - 2ab + 2b²
(3a - 2b)(a - b)
5ab (3a - 2b)
(3a - 2b)(a - b)
= 5ab
a - b

SECTION B: ATTEMPT ANY FIVE QUESTIONS IN THIS SECTION

Three points P, Q and S are pm the vertices of a triangular plain field. P is 400m from Q on a bearing of 3000 and R of 550m directly south of P.
1. Using a scale of 1 cm to represent 100m on the ground, draw a diagram to show the position of the points. (3mks)
  $14$
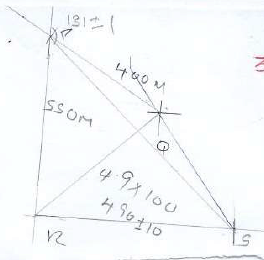
2. Use the scale drawing to determine;
  1. The distance and bearing of Q from R. (3mks)
    360 - 45 = 315º
    045º ± 1
    490 ± 10m
  2. The bearing and distance of point S from P given that point S is directly 600m East of R. (3mks)
    8 ± 1 x 100 = 80cm
    131º ± 1
  3. The bearing and distance of Q from S. (3mks)
    4.15 ± 1 x 100 = 415
    323º ± 1
A bus travelling at a speed of 80km/hr left Mombasa at 8.00am for Nairobi. Two hours later, a car travelling at a speed of 100km/hr left Nairobi for Mombasa.
Given that the distance between both cities is 500km, find the: -
1. distance covered by bus at the time the car is starting. (1mk)
  80 x 2 = 160km
2. Distance between the two vehicles at the time the is starting (1mk)
  500 - 160 = 340km
3. Relative speed of the two vehicles (1mk)
  100 + 80 = 180km/hr
4. Time taken for the two vehicles to meet (2mks)
  TK = 340
  180
  = 1.9
5. Time the met. (1mk)
  8 + 2 1.54mm
  11.54am
6. After meeting, the speed of both vehicles dropped to 60km/hr due to traffic jam. At what time did each vehicle arrive at its destination? (3mks)
  3.9 x 80 = 312 500 - 312
  188
  60
The kite shown on the fig below has vertices, A(-2,4)B(5,7)C (7,4) D(5,1).The kite ABCD is rotated about the origin through -90º to obtain its first image A’B’C’D’.The kite A’B’C’D’ is then reflected along the line = X = 0 to obtain A”B’’C’’D’’.Find
1. The equation of the Mirror line that reflects point A to itself, B on to D and C onto itself
2. Draw a kite A’B’C’D and state its coordinates.
A given solid is made up of a cone and three quarters of hemisphere as shown in the diagram below .The radius and vertical height of the cone are 4cm and 6.2 cm respectively
1. Calculate the volume of the solid (4mks)
  Volume sphere = ⁴/₃ πr³
  ⁴/₃x 3.15 x 4 x 4 x ¾ = 200.96
  Cone ¹/₃πr²h = ¹/₃x 3.14 x 4 x 4 x 6.2 = 103.83
  Total 304.89cm³
2. Calculate the surface area of the solid (4mks)
  Sphere 4πr²x ¾ = 4 x 3.14 x 4 x 4 x ¾
  = 150.816cm²
  Cone πrL = 3.142 x 7.348
  = 92.349 cm²
  Total = 243.166
3. The material used for making the solid costs shs 40 per cm3.What is the cost of making ten such solids (2mks)
  304.789 x 40 = 12191.56
In the diagram below, two circles, centres A and C and radii 7cm and 24cm respectively intersect at B and D. AC = 25cm.
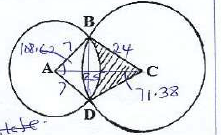
1. Show that angle ABC = 90º. (3mks)
  b² = a² + 6² - 2aCosB
  25² = 24² + 7² - 2.24 . 7CosB
  625 = 576 + 49 - 336CosB
  CosB = 623 - 625
  CosB = 0
  B = 90
2. Calculate
  1. the size of obtuse angle BAD (3mks)
    ½ x 7 x 24 = 84 x 2
    = 168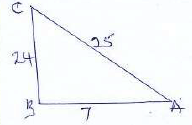
    $17$
    24² = 25² + 7² - 24 x 7cosA
    576 = 674 - 168 CosA
    +98 = +168CosA
    CosA = 0.5833
    A = 54.31º
    BAD = 108.62
  2. the area of the shaded part (4Mks)
    ½ x 7 x 24 x 2 = 168
    =108.62 x 3.142 x 2 x 7
    360
    = 13.27
    Shaded = 168 - 13.27
    = 154.73
Two lines L1=2y-3x-6 and L2=3y+x-20=0 intersect at point A.
1. Find the coordinates of A (3marks)
  (2y - 3x = 6) x 3
  (3y + x = 20) x 2
  6y - 9x = 18
  6y + 2x = 40
  -11x = -22
  x = 2
  1. A third line L₃ is perpendicular to L2 at point A. Find the equation of L₃ in form of y=mx+c, where m and c are constants. (3marks)
    3y = -x + 20
    y = - ¹/₃ x + ²⁰/₃
    m = 3
    y - 6 = 3
    x - 2
    y - 6 = 3x - 6
    y = 3x + 0
2. Another line L₄ is parallel to l1 and passes through (-1,3). Find the x-intercept and the y-intercept of L₄. (4marks)
  2y = 3x + 6
  y = ³/₂x + 3
  y - 3 = ³/₂
  x + 1
  2(y - 3) = 3(x + y)
  2y - 6 = 3x + 3
  2y = 3x + 9
  y = ³/₂x + 9
  x - intersept y =0
  ²/₃x x ³/₂x = ^-9/₂ x ²/₃
  x = -3
  y intercept 3a = 0
  y = ⁹/₂
  = 4.5
1. PQRS is a quadrilateral with vertices P(1,4), Q(2,1), R(2,3) and S(6,4). On the grid provided, plot the quadrilateral. (2mark)
2. Draw P’Q’R’S’ the image of PQRS under a positive quarter turn about the origin and write down its co-ordinates. (3 marks)
3. Draw P”Q”R”S” the image of P’Q’R’S’ under an enlargement scale factor -1 and center (0,0) and write down its co-ordinates. (3 marks)
  $18$
  Determine the single transformation that maps PQRS onto P”Q”R”S (2marks)